Model Reduction Techniques for Computing Approximately Optimal Solutions for Markov Decision Processes

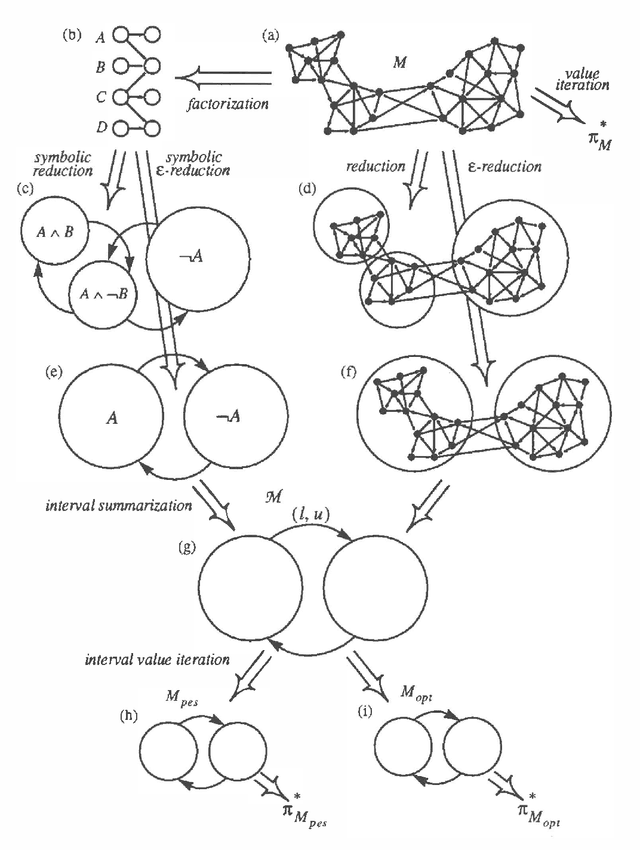
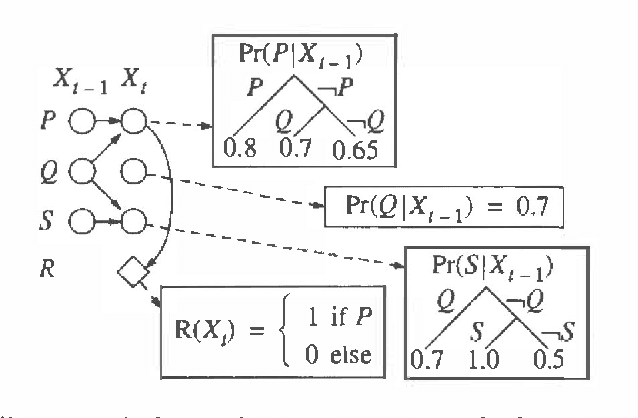
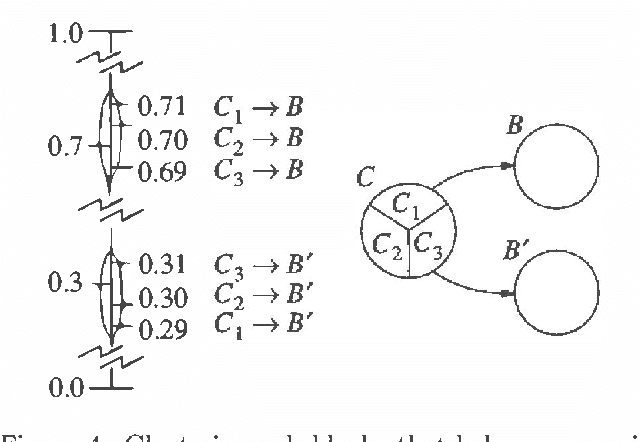
We present a method for solving implicit (factored) Markov decision processes (MDPs) with very large state spaces. We introduce a property of state space partitions which we call epsilon-homogeneity. Intuitively, an epsilon-homogeneous partition groups together states that behave approximately the same under all or some subset of policies. Borrowing from recent work on model minimization in computer-aided software verification, we present an algorithm that takes a factored representation of an MDP and an 0<=epsilon<=1 and computes a factored epsilon-homogeneous partition of the state space. This partition defines a family of related MDPs - those MDPs with state space equal to the blocks of the partition, and transition probabilities "approximately" like those of any (original MDP) state in the source block. To formally study such families of MDPs, we introduce the new notion of a "bounded parameter MDP" (BMDP), which is a family of (traditional) MDPs defined by specifying upper and lower bounds on the transition probabilities and rewards. We describe algorithms that operate on BMDPs to find policies that are approximately optimal with respect to the original MDP. In combination, our method for reducing a large implicit MDP to a possibly much smaller BMDP using an epsilon-homogeneous partition, and our methods for selecting actions in BMDPs constitute a new approach for analyzing large implicit MDPs. Among its advantages, this new approach provides insight into existing algorithms to solving implicit MDPs, provides useful connections to work in automata theory and model minimization, and suggests methods, which involve varying epsilon, to trade time and space (specifically in terms of the size of the corresponding state space) for solution quality.