Incremental Pruning: A Simple, Fast, Exact Method for Partially Observable Markov Decision Processes

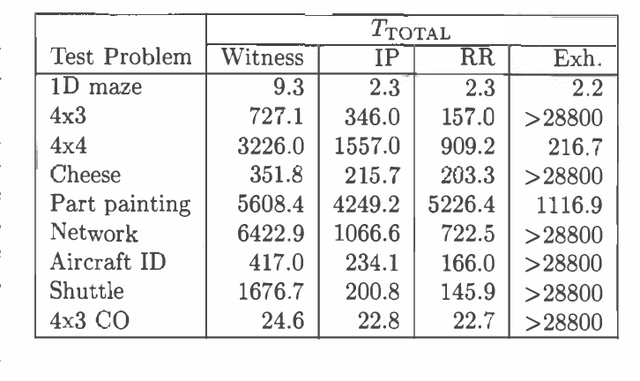
Most exact algorithms for general partially observable Markov decision processes (POMDPs) use a form of dynamic programming in which a piecewise-linear and convex representation of one value function is transformed into another. We examine variations of the "incremental pruning" method for solving this problem and compare them to earlier algorithms from theoretical and empirical perspectives. We find that incremental pruning is presently the most efficient exact method for solving POMDPs.

Solving POMDPs by Searching the Space of Finite Policies

Solving partially observable Markov decision processes (POMDPs) is highly intractable in general, at least in part because the optimal policy may be infinitely large. In this paper, we explore the problem of finding the optimal policy from a restricted set of policies, represented as finite state automata of a given size. This problem is also intractable, but we show that the complexity can be greatly reduced when the POMDP and/or policy are further constrained. We demonstrate good empirical results with a branch-and-bound method for finding globally optimal deterministic policies, and a gradient-ascent method for finding locally optimal stochastic policies.