Learning the Structure of Auto-Encoding Recommenders

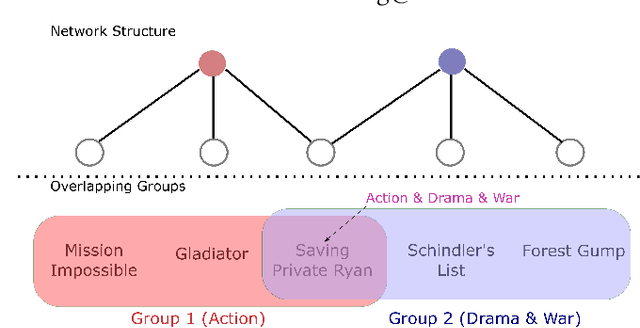
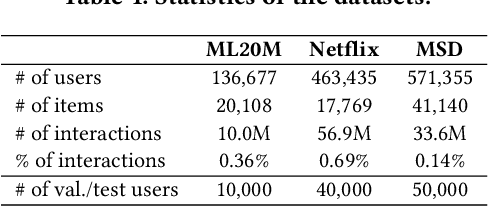
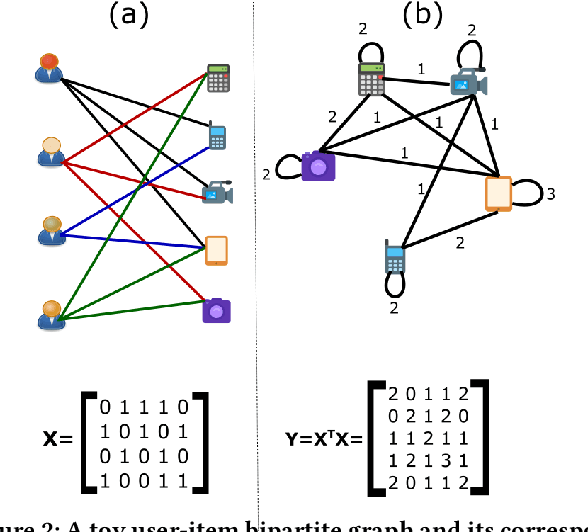
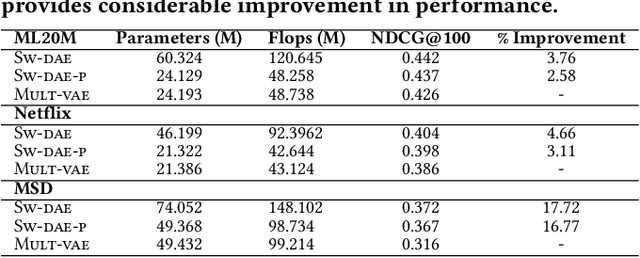
Autoencoder recommenders have recently shown state-of-the-art performance in the recommendation task due to their ability to model non-linear item relationships effectively. However, existing autoencoder recommenders use fully-connected neural network layers and do not employ structure learning. This can lead to inefficient training, especially when the data is sparse as commonly found in collaborative filtering. The aforementioned results in lower generalization ability and reduced performance. In this paper, we introduce structure learning for autoencoder recommenders by taking advantage of the inherent item groups present in the collaborative filtering domain. Due to the nature of items in general, we know that certain items are more related to each other than to other items. Based on this, we propose a method that first learns groups of related items and then uses this information to determine the connectivity structure of an auto-encoding neural network. This results in a network that is sparsely connected. This sparse structure can be viewed as a prior that guides the network training. Empirically we demonstrate that the proposed structure learning enables the autoencoder to converge to a local optimum with a much smaller spectral norm and generalization error bound than the fully-connected network. The resultant sparse network considerably outperforms the state-of-the-art methods like \textsc{Mult-vae/Mult-dae} on multiple benchmarked datasets even when the same number of parameters and flops are used. It also has a better cold-start performance.

Sidestepping the Triangulation Problem in Bayesian Net Computations

This paper presents a new approach for computing posterior probabilities in Bayesian nets, which sidesteps the triangulation problem. The current state of art is the clique tree propagation approach. When the underlying graph of a Bayesian net is triangulated, this approach arranges its cliques into a tree and computes posterior probabilities by appropriately passing around messages in that tree. The computation in each clique is simply direct marginalization. When the underlying graph is not triangulated, one has to first triangulated it by adding edges. Referred to as the triangulation problem, the problem of finding an optimal or even a ?good? triangulation proves to be difficult. In this paper, we propose to first decompose a Bayesian net into smaller components by making use of Tarjan's algorithm for decomposing an undirected graph at all its minimal complete separators. Then, the components are arranged into a tree and posterior probabilities are computed by appropriately passing around messages in that tree. The computation in each component is carried out by repeating the whole procedure from the beginning. Thus the triangulation problem is sidestepped.

Incremental computation of the value of perfect information in stepwise-decomposable influence diagrams

To determine the value of perfect information in an influence diagram, one needs first to modify the diagram to reflect the change in information availability, and then to compute the optimal expected values of both the original diagram and the modified diagram. The value of perfect information is the difference between the two optimal expected values. This paper is about how to speed up the computation of the optimal expected value of the modified diagram by making use of the intermediate computation results obtained when computing the optimal expected value of the original diagram.

Inter-causal Independence and Heterogeneous Factorization

It is well known that conditional independence can be used to factorize a joint probability into a multiplication of conditional probabilities. This paper proposes a constructive definition of inter-causal independence, which can be used to further factorize a conditional probability. An inference algorithm is developed, which makes use of both conditional independence and inter-causal independence to reduce inference complexity in Bayesian networks.

Solving Asymmetric Decision Problems with Influence Diagrams

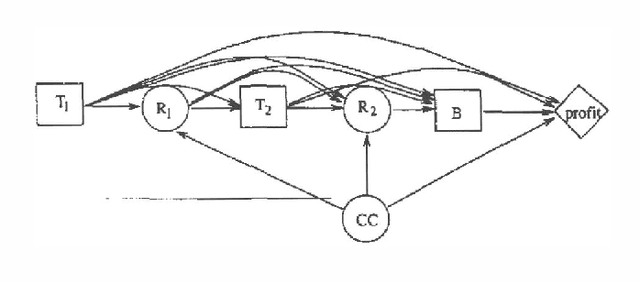
While influence diagrams have many advantages as a representation framework for Bayesian decision problems, they have a serious drawback in handling asymmetric decision problems. To be represented in an influence diagram, an asymmetric decision problem must be symmetrized. A considerable amount of unnecessary computation may be involved when a symmetrized influence diagram is evaluated by conventional algorithms. In this paper we present an approach for avoiding such unnecessary computation in influence diagram evaluation.

Inference with Causal Independence in the CPSC Network

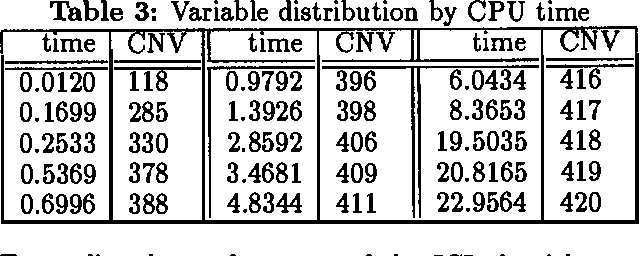
This paper reports experiments with the causal independence inference algorithm proposed by Zhang and Poole (1994b) on the CPSC network created by Pradhan et al. (1994). It is found that the algorithm is able to answer 420 of the 422 possible zero-observation queries, 94 of 100 randomly generated five-observation queries, 87 of 100 randomly generated ten-observation queries, and 69 of 100 randomly generated twenty-observation queries.

Fast Value Iteration for Goal-Directed Markov Decision Processes

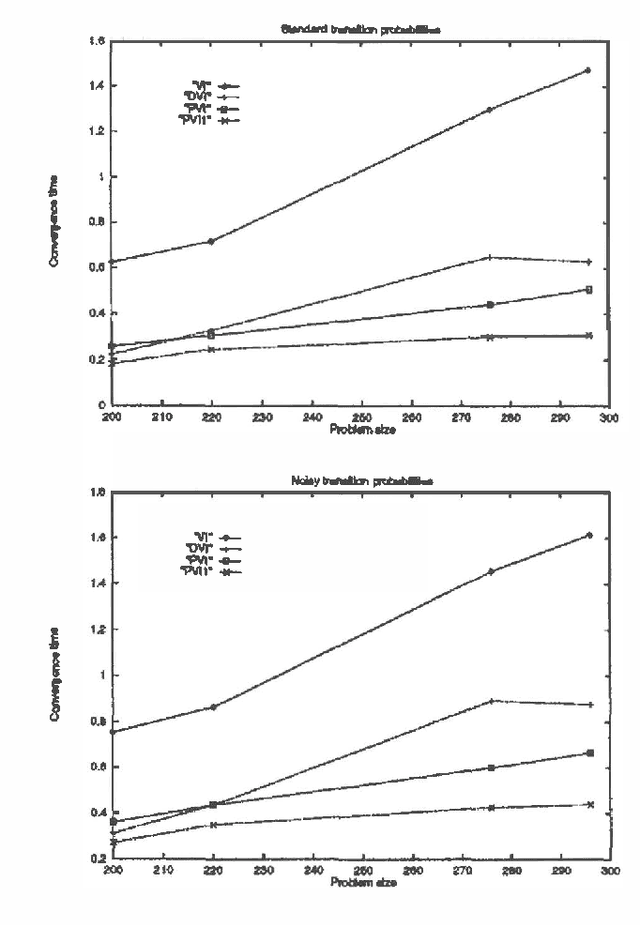
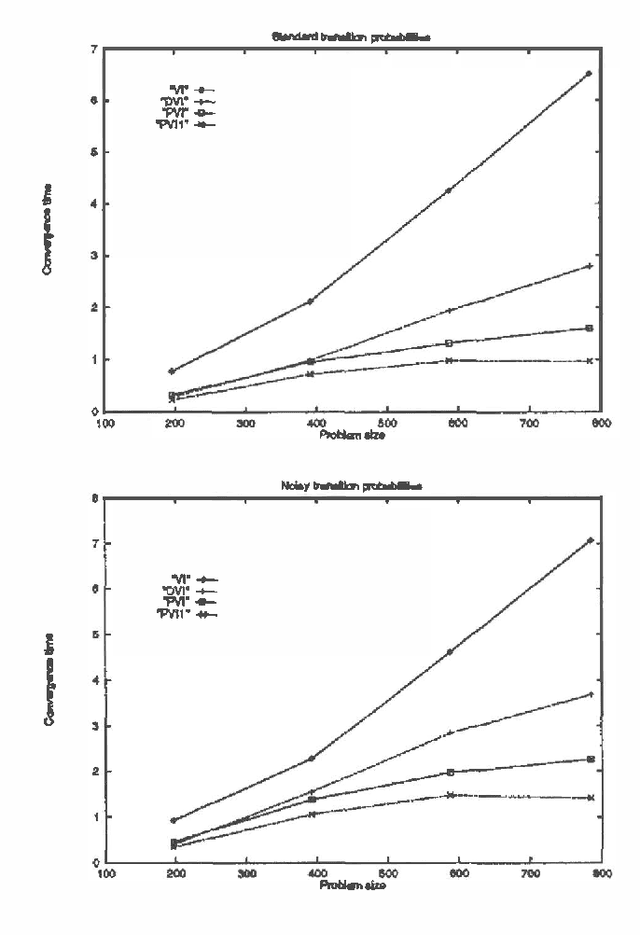
Planning problems where effects of actions are non-deterministic can be modeled as Markov decision processes. Planning problems are usually goal-directed. This paper proposes several techniques for exploiting the goal-directedness to accelerate value iteration, a standard algorithm for solving Markov decision processes. Empirical studies have shown that the techniques can bring about significant speedups.

Independence of Causal Influence and Clique Tree Propagation

This paper explores the role of independence of causal influence (ICI) in Bayesian network inference. ICI allows one to factorize a conditional probability table into smaller pieces. We describe a method for exploiting the factorization in clique tree propagation (CTP) - the state-of-the-art exact inference algorithm for Bayesian networks. We also present empirical results showing that the resulting algorithm is significantly more efficient than the combination of CTP and previous techniques for exploiting ICI.

Region-Based Approximations for Planning in Stochastic Domains

This paper is concerned with planning in stochastic domains by means of partially observable Markov decision processes (POMDPs). POMDPs are difficult to solve. This paper identifies a subclass of POMDPs called region observable POMDPs, which are easier to solve and can be used to approximate general POMDPs to arbitrary accuracy.

Incremental Pruning: A Simple, Fast, Exact Method for Partially Observable Markov Decision Processes

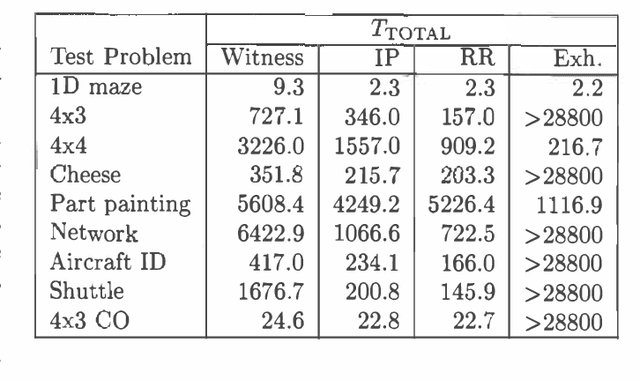
Most exact algorithms for general partially observable Markov decision processes (POMDPs) use a form of dynamic programming in which a piecewise-linear and convex representation of one value function is transformed into another. We examine variations of the "incremental pruning" method for solving this problem and compare them to earlier algorithms from theoretical and empirical perspectives. We find that incremental pruning is presently the most efficient exact method for solving POMDPs.