Towards Solving the Multiple Extension Problem: Combining Defaults and Probabilities

The multiple extension problem arises frequently in diagnostic and default inference. That is, we can often use any of a number of sets of defaults or possible hypotheses to explain observations or make Predictions. In default inference, some extensions seem to be simply wrong and we use qualitative techniques to weed out the unwanted ones. In the area of diagnosis, however, the multiple explanations may all seem reasonable, however improbable. Choosing among them is a matter of quantitative preference. Quantitative preference works well in diagnosis when knowledge is modelled causally. Here we suggest a framework that combines probabilities and defaults in a single unified framework that retains the semantics of diagnosis as construction of explanations from a fixed set of possible hypotheses. We can then compute probabilities incrementally as we construct explanations. Here we describe a branch and bound algorithm that maintains a set of all partial explanations while exploring a most promising one first. A most probable explanation is found first if explanations are partially ordered.

Probabilistic Semantics and Defaults

There is much interest in providing probabilistic semantics for defaults but most approaches seem to suffer from one of two problems: either they require numbers, a problem defaults were intended to avoid, or they generate peculiar side effects. Rather than provide semantics for defaults, we address the problem defaults were intended to solve: that of reasoning under uncertainty where numeric probability distributions are not available. We describe a non-numeric formalism called an inference graph based on standard probability theory, conditional independence and sentences of favouring where a favours b - favours(a, b) - p(a|b) > p(a). The formalism seems to handle the examples from the nonmonotonic literature. Most importantly, the sentences of our system can be verified by performing an appropriate experiment in the semantic domain.

Can Uncertainty Management be Realized in a Finite Totally Ordered Probability Algebra?

In this paper, the feasibility of using finite totally ordered probability models under Alelinnas's Theory of Probabilistic Logic [Aleliunas, 1988] is investigated. The general form of the probability algebra of these models is derived and the number of possible algebras with given size is deduced. Based on this analysis, we discuss problems of denominator-indifference and ambiguity-generation that arise in reasoning by cases and abductive reasoning. An example is given that illustrates how these problems arise. The investigation shows that a finite probability model may be of very limited usage.

Inter-causal Independence and Heterogeneous Factorization

It is well known that conditional independence can be used to factorize a joint probability into a multiplication of conditional probabilities. This paper proposes a constructive definition of inter-causal independence, which can be used to further factorize a conditional probability. An inference algorithm is developed, which makes use of both conditional independence and inter-causal independence to reduce inference complexity in Bayesian networks.

Symmetric Collaborative Filtering Using the Noisy Sensor Model

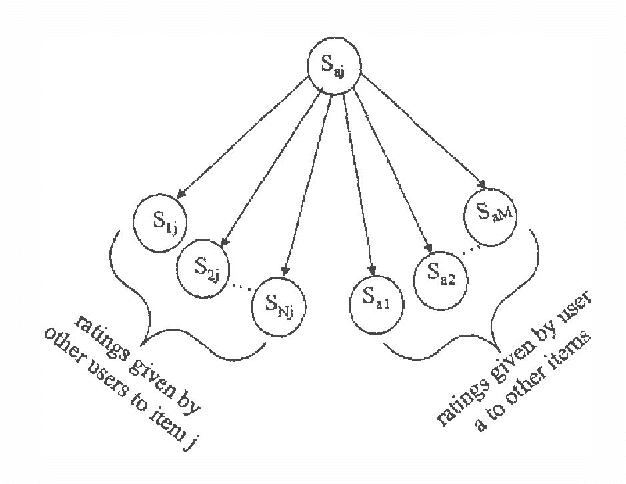
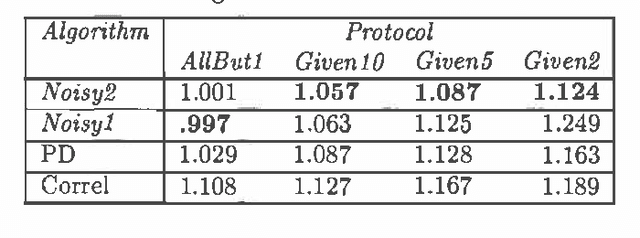
Collaborative filtering is the process of making recommendations regarding the potential preference of a user, for example shopping on the Internet, based on the preference ratings of the user and a number of other users for various items. This paper considers collaborative filtering based on explicitmulti-valued ratings. To evaluate the algorithms, weconsider only {em pure} collaborative filtering, using ratings exclusively, and no other information about the people or items.Our approach is to predict a user's preferences regarding a particularitem by using other people who rated that item and other items ratedby the user as noisy sensors. The noisy sensor model uses Bayes' theorem to compute the probability distribution for the user'srating of a new item. We give two variant models: in one, we learn a{em classical normal linear regression} model of how users rate items; in another,we assume different users rate items the same, but the accuracy of thesensors needs to be learned. We compare these variant models withstate-of-the-art techniques and show how they are significantly better,whether a user has rated only two items or many. We reportempirical results using the EachMovie database footnote{http://research.compaq.com/SRC/eachmovie/} of movie ratings. Wealso show that by considering items similarity along with theusers similarity, the accuracy of the prediction increases.

Efficient Inference in Large Discrete Domains

In this paper we examine the problem of inference in Bayesian Networks with discrete random variables that have very large or even unbounded domains. For example, in a domain where we are trying to identify a person, we may have variables that have as domains, the set of all names, the set of all postal codes, or the set of all credit card numbers. We cannot just have big tables of the conditional probabilities, but need compact representations. We provide an inference algorithm, based on variable elimination, for belief networks containing both large domain and normal discrete random variables. We use intensional (i.e., in terms of procedures) and extensional (in terms of listing the elements) representations of conditional probabilities and of the intermediate factors.

Nonparametric Bayesian Logic

The Bayesian Logic (BLOG) language was recently developed for defining first-order probability models over worlds with unknown numbers of objects. It handles important problems in AI, including data association and population estimation. This paper extends BLOG by adopting generative processes over function spaces - known as nonparametrics in the Bayesian literature. We introduce syntax for reasoning about arbitrary collections of objects, and their properties, in an intuitive manner. By exploiting exchangeability, distributions over unknown objects and their attributes are cast as Dirichlet processes, which resolve difficulties in model selection and inference caused by varying numbers of objects. We demonstrate these concepts with application to citation matching.

Constraint Processing in Lifted Probabilistic Inference

First-order probabilistic models combine representational power of first-order logic with graphical models. There is an ongoing effort to design lifted inference algorithms for first-order probabilistic models. We analyze lifted inference from the perspective of constraint processing and, through this viewpoint, we analyze and compare existing approaches and expose their advantages and limitations. Our theoretical results show that the wrong choice of constraint processing method can lead to exponential increase in computational complexity. Our empirical tests confirm the importance of constraint processing in lifted inference. This is the first theoretical and empirical study of constraint processing in lifted inference.

Seeing the Forest Despite the Trees: Large Scale Spatial-Temporal Decision Making

We introduce a challenging real-world planning problem where actions must be taken at each location in a spatial area at each point in time. We use forestry planning as the motivating application. In Large Scale Spatial-Temporal (LSST) planning problems, the state and action spaces are defined as the cross-products of many local state and action spaces spread over a large spatial area such as a city or forest. These problems possess state uncertainty, have complex utility functions involving spatial constraints and we generally must rely on simulations rather than an explicit transition model. We define LSST problems as reinforcement learning problems and present a solution using policy gradients. We compare two different policy formulations: an explicit policy that identifies each location in space and the action to take there; and an abstract policy that defines the proportion of actions to take across all locations in space. We show that the abstract policy is more robust and achieves higher rewards with far fewer parameters than the elementary policy. This abstract policy is also a better fit to the properties that practitioners in LSST problem domains require for such methods to be widely useful.