Disentanglement in Implicit Causal Models via Switch Variable

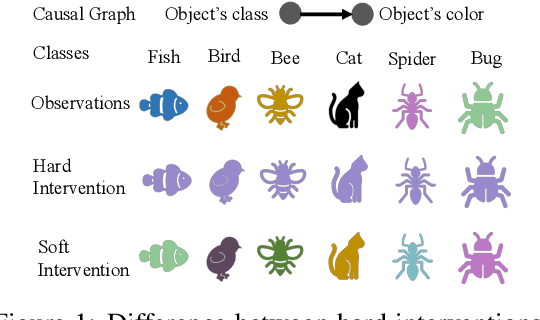
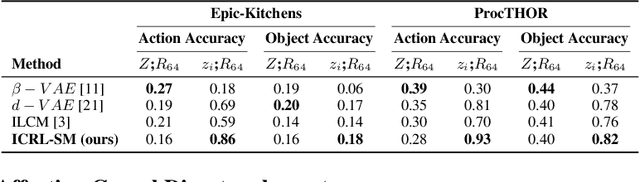
Learning causal representations from observational and interventional data in the absence of known ground-truth graph structures necessitates implicit latent causal representation learning. Implicitly learning causal mechanisms typically involves two categories of interventional data: hard and soft interventions. In real-world scenarios, soft interventions are often more realistic than hard interventions, as the latter require fully controlled environments. Unlike hard interventions, which directly force changes in a causal variable, soft interventions exert influence indirectly by affecting the causal mechanism. In this paper, we tackle implicit latent causal representation learning in a Variational Autoencoder (VAE) framework through soft interventions. Our approach models soft interventions effects by employing a causal mechanism switch variable designed to toggle between different causal mechanisms. In our experiments, we consistently observe improved learning of identifiable, causal representations, compared to baseline approaches.

Learning when to observe: A frugal reinforcement learning framework for a high-cost world

Reinforcement learning (RL) has been shown to learn sophisticated control policies for complex tasks including games, robotics, heating and cooling systems and text generation. The action-perception cycle in RL, however, generally assumes that a measurement of the state of the environment is available at each time step without a cost. In applications such as materials design, deep-sea and planetary robot exploration and medicine, however, there can be a high cost associated with measuring, or even approximating, the state of the environment. In this paper, we survey the recently growing literature that adopts the perspective that an RL agent might not need, or even want, a costly measurement at each time step. Within this context, we propose the Deep Dynamic Multi-Step Observationless Agent (DMSOA), contrast it with the literature and empirically evaluate it on OpenAI gym and Atari Pong environments. Our results, show that DMSOA learns a better policy with fewer decision steps and measurements than the considered alternative from the literature. The corresponding code is available at: \url{https://github.com/cbellinger27/Learning-when-to-observe-in-RL

ChemGymRL: An Interactive Framework for Reinforcement Learning for Digital Chemistry

This paper provides a simulated laboratory for making use of Reinforcement Learning (RL) for chemical discovery. Since RL is fairly data intensive, training agents `on-the-fly' by taking actions in the real world is infeasible and possibly dangerous. Moreover, chemical processing and discovery involves challenges which are not commonly found in RL benchmarks and therefore offer a rich space to work in. We introduce a set of highly customizable and open-source RL environments, ChemGymRL, based on the standard Open AI Gym template. ChemGymRL supports a series of interconnected virtual chemical benches where RL agents can operate and train. The paper introduces and details each of these benches using well-known chemical reactions as illustrative examples, and trains a set of standard RL algorithms in each of these benches. Finally, discussion and comparison of the performances of several standard RL methods are provided in addition to a list of directions for future work as a vision for the further development and usage of ChemGymRL.

Generative Causal Representation Learning for Out-of-Distribution Motion Forecasting

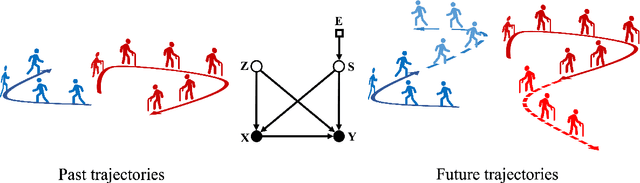
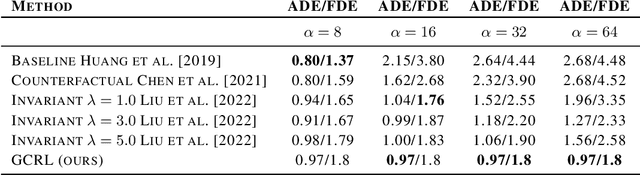
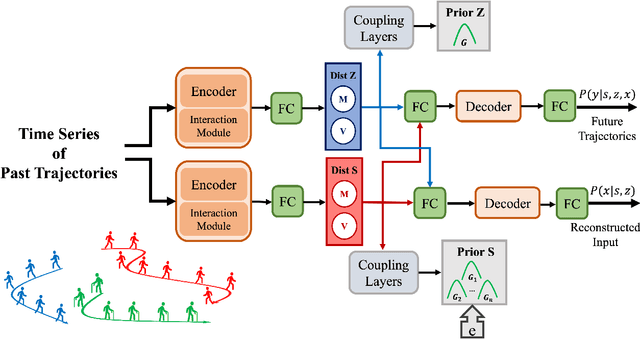
Conventional supervised learning methods typically assume i.i.d samples and are found to be sensitive to out-of-distribution (OOD) data. We propose Generative Causal Representation Learning (GCRL) which leverages causality to facilitate knowledge transfer under distribution shifts. While we evaluate the effectiveness of our proposed method in human trajectory prediction models, GCRL can be applied to other domains as well. First, we propose a novel causal model that explains the generative factors in motion forecasting datasets using features that are common across all environments and with features that are specific to each environment. Selection variables are used to determine which parts of the model can be directly transferred to a new environment without fine-tuning. Second, we propose an end-to-end variational learning paradigm to learn the causal mechanisms that generate observations from features. GCRL is supported by strong theoretical results that imply identifiability of the causal model under certain assumptions. Experimental results on synthetic and real-world motion forecasting datasets show the robustness and effectiveness of our proposed method for knowledge transfer under zero-shot and low-shot settings by substantially outperforming the prior motion forecasting models on out-of-distribution prediction.

Learning from Multiple Independent Advisors in Multi-agent Reinforcement Learning

Multi-agent reinforcement learning typically suffers from the problem of sample inefficiency, where learning suitable policies involves the use of many data samples. Learning from external demonstrators is a possible solution that mitigates this problem. However, most prior approaches in this area assume the presence of a single demonstrator. Leveraging multiple knowledge sources (i.e., advisors) with expertise in distinct aspects of the environment could substantially speed up learning in complex environments. This paper considers the problem of simultaneously learning from multiple independent advisors in multi-agent reinforcement learning. The approach leverages a two-level Q-learning architecture, and extends this framework from single-agent to multi-agent settings. We provide principled algorithms that incorporate a set of advisors by both evaluating the advisors at each state and subsequently using the advisors to guide action selection. We also provide theoretical convergence and sample complexity guarantees. Experimentally, we validate our approach in three different test-beds and show that our algorithms give better performances than baselines, can effectively integrate the combined expertise of different advisors, and learn to ignore bad advice.

Using Affect as a Communication Modality to Improve Human-Robot Communication in Robot-Assisted Search and Rescue Scenarios

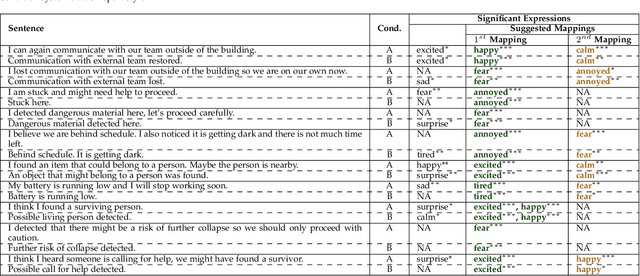
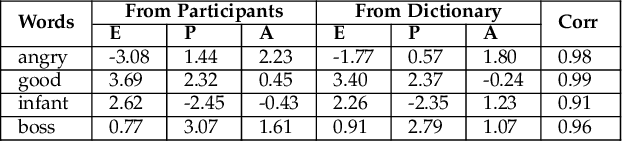
Emotions can provide a natural communication modality to complement the existing multi-modal capabilities of social robots, such as text and speech, in many domains. We conducted three online studies with 112, 223, and 151 participants to investigate the benefits of using emotions as a communication modality for Search And Rescue (SAR) robots. In the first experiment, we investigated the feasibility of conveying information related to SAR situations through robots' emotions, resulting in mappings from SAR situations to emotions. The second study used Affect Control Theory as an alternative method for deriving such mappings. This method is more flexible, e.g. allows for such mappings to be adjusted for different emotion sets and different robots. In the third experiment, we created affective expressions for an appearance-constrained outdoor field research robot using LEDs as an expressive channel. Using these affective expressions in a variety of simulated SAR situations, we evaluated the effect of these expressions on participants' (adopting the role of rescue workers) situational awareness. Our results and proposed methodologies provide (a) insights on how emotions could help conveying messages in the context of SAR, and (b) evidence on the effectiveness of adding emotions as a communication modality in a (simulated) SAR communication context.

Theoretical Connection between Locally Linear Embedding, Factor Analysis, and Probabilistic PCA

Locally Linear Embedding (LLE) is a nonlinear spectral dimensionality reduction and manifold learning method. It has two main steps which are linear reconstruction and linear embedding of points in the input space and embedding space, respectively. In this work, we look at the linear reconstruction step from a stochastic perspective where it is assumed that every data point is conditioned on its linear reconstruction weights as latent factors. The stochastic linear reconstruction of LLE is solved using expectation maximization. We show that there is a theoretical connection between three fundamental dimensionality reduction methods, i.e., LLE, factor analysis, and probabilistic Principal Component Analysis (PCA). The stochastic linear reconstruction of LLE is formulated similar to the factor analysis and probabilistic PCA. It is also explained why factor analysis and probabilistic PCA are linear and LLE is a nonlinear method. This work combines and makes a bridge between two broad approaches of dimensionality reduction, i.e., the spectral and probabilistic algorithms.

On Manifold Hypothesis: Hypersurface Submanifold Embedding Using Osculating Hyperspheres

Consider a set of $n$ data points in the Euclidean space $\mathbb{R}^d$. This set is called dataset in machine learning and data science. Manifold hypothesis states that the dataset lies on a low-dimensional submanifold with high probability. All dimensionality reduction and manifold learning methods have the assumption of manifold hypothesis. In this paper, we show that the dataset lies on an embedded hypersurface submanifold which is locally $(d-1)$-dimensional. Hence, we show that the manifold hypothesis holds at least for the embedding dimensionality $d-1$. Using an induction in a pyramid structure, we also extend the embedding dimensionality to lower embedding dimensionalities to show the validity of manifold hypothesis for embedding dimensionalities $\{1, 2, \dots, d-1\}$. For embedding the hypersurface, we first construct the $d$ nearest neighbors graph for data. For every point, we fit an osculating hypersphere $S^{d-1}$ using its neighbors where this hypersphere is osculating to a hypothetical hypersurface. Then, using surgery theory, we apply surgery on the osculating hyperspheres to obtain $n$ hyper-caps. We connect the hyper-caps to one another using partial hyper-cylinders. By connecting all parts, the embedded hypersurface is obtained as the disjoint union of these elements. We discuss the geometrical characteristics of the embedded hypersurface, such as having boundary, its topology, smoothness, boundedness, orientability, compactness, and injectivity. Some discussion are also provided for the linearity and structure of data. This paper is the intersection of several fields of science including machine learning, differential geometry, and algebraic topology.

Spectral, Probabilistic, and Deep Metric Learning: Tutorial and Survey

This is a tutorial and survey paper on metric learning. Algorithms are divided into spectral, probabilistic, and deep metric learning. We first start with the definition of distance metric, Mahalanobis distance, and generalized Mahalanobis distance. In spectral methods, we start with methods using scatters of data, including the first spectral metric learning, relevant methods to Fisher discriminant analysis, Relevant Component Analysis (RCA), Discriminant Component Analysis (DCA), and the Fisher-HSIC method. Then, large-margin metric learning, imbalanced metric learning, locally linear metric adaptation, and adversarial metric learning are covered. We also explain several kernel spectral methods for metric learning in the feature space. We also introduce geometric metric learning methods on the Riemannian manifolds. In probabilistic methods, we start with collapsing classes in both input and feature spaces and then explain the neighborhood component analysis methods, Bayesian metric learning, information theoretic methods, and empirical risk minimization in metric learning. In deep learning methods, we first introduce reconstruction autoencoders and supervised loss functions for metric learning. Then, Siamese networks and its various loss functions, triplet mining, and triplet sampling are explained. Deep discriminant analysis methods, based on Fisher discriminant analysis, are also reviewed. Finally, we introduce multi-modal deep metric learning, geometric metric learning by neural networks, and few-shot metric learning.

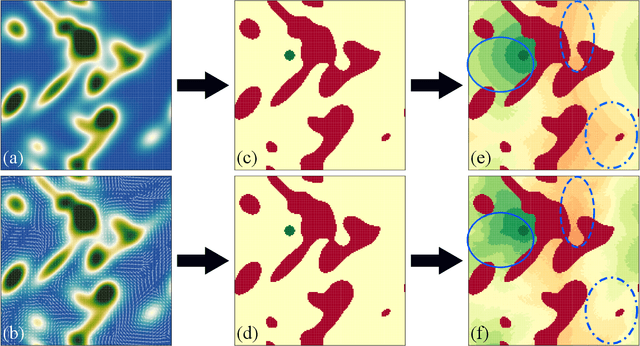
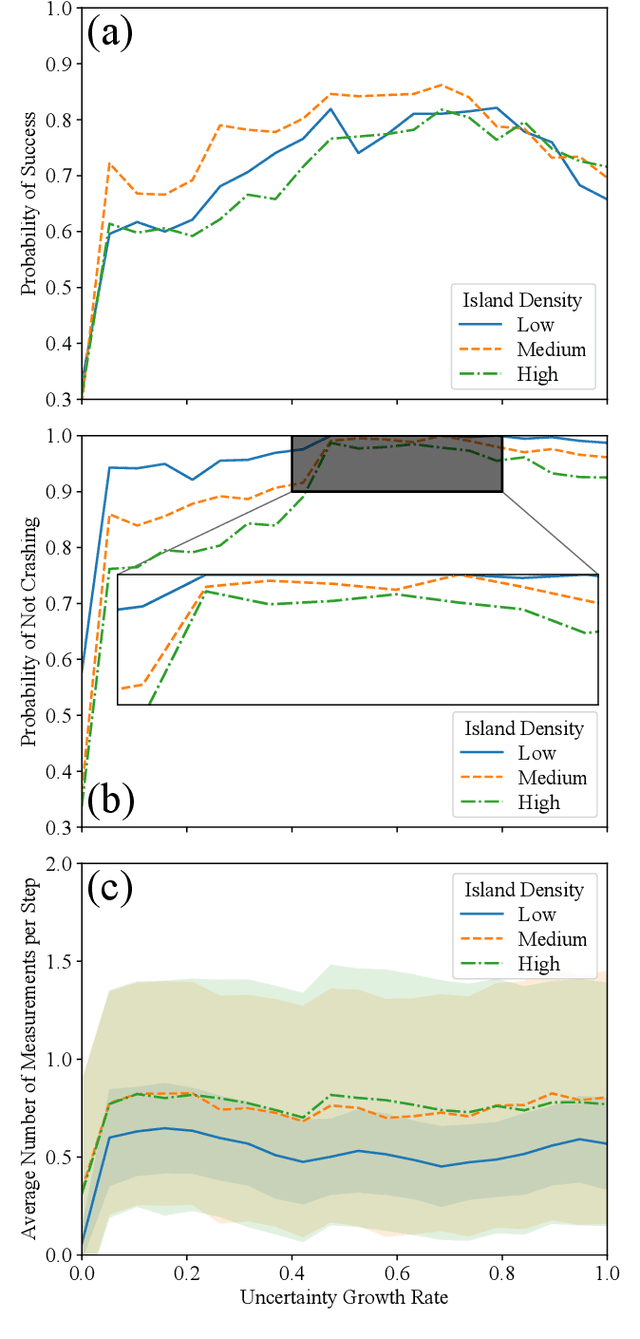
Dynamic programming with partial information to overcome navigational uncertainty in a nautical environment

Using a toy nautical navigation environment, we show that dynamic programming can be used when only partial information about a partially observed Markov decision process (POMDP) is known. By incorporating uncertainty into our model, we show that navigation policies can be constructed that maintain safety. Adding controlled sensing methods, we show that these policies can also lower measurement costs at the same time.