From Graph Diffusion to Graph Classification

Generative models such as diffusion models have achieved remarkable success in state-of-the-art image and text tasks. Recently, score-based diffusion models have extended their success beyond image generation, showing competitive performance with discriminative methods in image {\em classification} tasks~\cite{zimmermann2021score}. However, their application to classification in the {\em graph} domain, which presents unique challenges such as complex topologies, remains underexplored. We show how graph diffusion models can be applied for graph classification. We find that to achieve competitive classification accuracy, score-based graph diffusion models should be trained with a novel training objective that is tailored to graph classification. In experiments with a sampling-based inference method, our discriminative training objective achieves state-of-the-art graph classification accuracy.

Deep Generative Models for Subgraph Prediction

Graph Neural Networks (GNNs) are important across different domains, such as social network analysis and recommendation systems, due to their ability to model complex relational data. This paper introduces subgraph queries as a new task for deep graph learning. Unlike traditional graph prediction tasks that focus on individual components like link prediction or node classification, subgraph queries jointly predict the components of a target subgraph based on evidence that is represented by an observed subgraph. For instance, a subgraph query can predict a set of target links and/or node labels. To answer subgraph queries, we utilize a probabilistic deep Graph Generative Model. Specifically, we inductively train a Variational Graph Auto-Encoder (VGAE) model, augmented to represent a joint distribution over links, node features and labels. Bayesian optimization is used to tune a weighting for the relative importance of links, node features and labels in a specific domain. We describe a deterministic and a sampling-based inference method for estimating subgraph probabilities from the VGAE generative graph distribution, without retraining, in zero-shot fashion. For evaluation, we apply the inference methods on a range of subgraph queries on six benchmark datasets. We find that inference from a model achieves superior predictive performance, surpassing independent prediction baselines with improvements in AUC scores ranging from 0.06 to 0.2 points, depending on the dataset.

Why Online Reinforcement Learning is Causal

Reinforcement learning (RL) and causal modelling naturally complement each other. The goal of causal modelling is to predict the effects of interventions in an environment, while the goal of reinforcement learning is to select interventions that maximize the rewards the agent receives from the environment. Reinforcement learning includes the two most powerful sources of information for estimating causal relationships: temporal ordering and the ability to act on an environment. This paper examines which reinforcement learning settings we can expect to benefit from causal modelling, and how. In online learning, the agent has the ability to interact directly with their environment, and learn from exploring it. Our main argument is that in online learning, conditional probabilities are causal, and therefore offline RL is the setting where causal learning has the most potential to make a difference. Essentially, the reason is that when an agent learns from their {\em own} experience, there are no unobserved confounders that influence both the agent's own exploratory actions and the rewards they receive. Our paper formalizes this argument. For offline RL, where an agent may and typically does learn from the experience of {\em others}, we describe previous and new methods for leveraging a causal model, including support for counterfactual queries.

Disentanglement in Implicit Causal Models via Switch Variable

Learning causal representations from observational and interventional data in the absence of known ground-truth graph structures necessitates implicit latent causal representation learning. Implicitly learning causal mechanisms typically involves two categories of interventional data: hard and soft interventions. In real-world scenarios, soft interventions are often more realistic than hard interventions, as the latter require fully controlled environments. Unlike hard interventions, which directly force changes in a causal variable, soft interventions exert influence indirectly by affecting the causal mechanism. In this paper, we tackle implicit latent causal representation learning in a Variational Autoencoder (VAE) framework through soft interventions. Our approach models soft interventions effects by employing a causal mechanism switch variable designed to toggle between different causal mechanisms. In our experiments, we consistently observe improved learning of identifiable, causal representations, compared to baseline approaches.

Computing Expected Motif Counts for Exchangeable Graph Generative Models

Estimating the expected value of a graph statistic is an important inference task for using and learning graph models. This note presents a scalable estimation procedure for expected motif counts, a widely used type of graph statistic. The procedure applies for generative mixture models of the type used in neural and Bayesian approaches to graph data.

Generative Causal Representation Learning for Out-of-Distribution Motion Forecasting

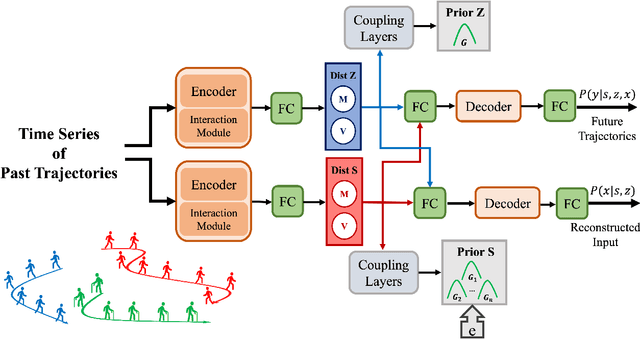
Conventional supervised learning methods typically assume i.i.d samples and are found to be sensitive to out-of-distribution (OOD) data. We propose Generative Causal Representation Learning (GCRL) which leverages causality to facilitate knowledge transfer under distribution shifts. While we evaluate the effectiveness of our proposed method in human trajectory prediction models, GCRL can be applied to other domains as well. First, we propose a novel causal model that explains the generative factors in motion forecasting datasets using features that are common across all environments and with features that are specific to each environment. Selection variables are used to determine which parts of the model can be directly transferred to a new environment without fine-tuning. Second, we propose an end-to-end variational learning paradigm to learn the causal mechanisms that generate observations from features. GCRL is supported by strong theoretical results that imply identifiability of the causal model under certain assumptions. Experimental results on synthetic and real-world motion forecasting datasets show the robustness and effectiveness of our proposed method for knowledge transfer under zero-shot and low-shot settings by substantially outperforming the prior motion forecasting models on out-of-distribution prediction.

From Graph Generation to Graph Classification

This note describes a new approach to classifying graphs that leverages graph generative models (GGM). Assuming a GGM that defines a joint probability distribution over graphs and their class labels, I derive classification formulas for the probability of a class label given a graph. A new conditional ELBO can be used to train a generative graph auto-encoder model for discrimination. While leveraging generative models for classification has been well explored for non-relational i.i.d. data, to our knowledge it is a novel approach to graph classification.

Cause-Effect Inference in Location-Scale Noise Models: Maximum Likelihood vs. Independence Testing

Location-scale noise models (LSNMs) are a class of heteroscedastic structural causal models with wide applicability, closely related to affine flow models. Recent likelihood-based methods designed for LSNMs that infer cause-effect relationships achieve state-of-the-art accuracy, when their assumptions are satisfied concerning the noise distributions. However, under misspecification their accuracy deteriorates sharply, especially when the conditional variance in the anti-causal direction is smaller than that in the causal direction. In this paper, we demonstrate the misspecification problem and analyze why and when it occurs. We show that residual independence testing is much more robust to misspecification than likelihood-based cause-effect inference. Our empirical evaluation includes 580 synthetic and 99 real-world datasets.

Micro and Macro Level Graph Modeling for Graph Variational Auto-Encoders

Generative models for graph data are an important research topic in machine learning. Graph data comprise two levels that are typically analyzed separately: node-level properties such as the existence of a link between a pair of nodes, and global aggregate graph-level statistics, such as motif counts. This paper proposes a new multi-level framework that jointly models node-level properties and graph-level statistics, as mutually reinforcing sources of information. We introduce a new micro-macro training objective for graph generation that combines node-level and graph-level losses. We utilize the micro-macro objective to improve graph generation with a GraphVAE, a well-established model based on graph-level latent variables, that provides fast training and generation time for medium-sized graphs. Our experiments show that adding micro-macro modeling to the GraphVAE model improves graph quality scores up to 2 orders of magnitude on five benchmark datasets, while maintaining the GraphVAE generation speed advantage.

Pre and Post Counting for Scalable Statistical-Relational Model Discovery

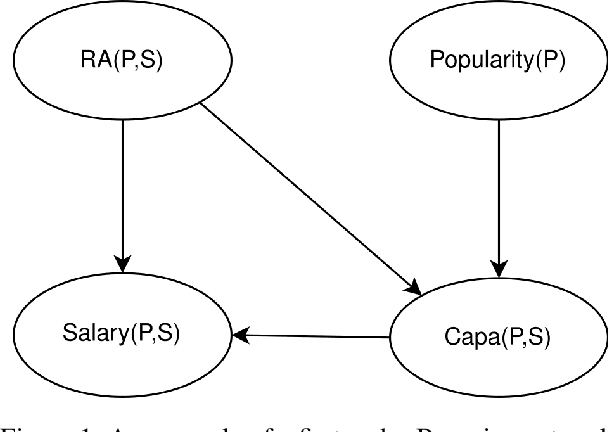
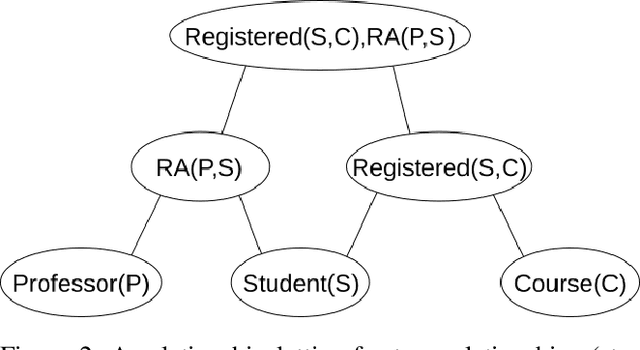
Statistical-Relational Model Discovery aims to find statistically relevant patterns in relational data. For example, a relational dependency pattern may stipulate that a user's gender is associated with the gender of their friends. As with propositional (non-relational) graphical models, the major scalability bottleneck for model discovery is computing instantiation counts: the number of times a relational pattern is instantiated in a database. Previous work on propositional learning utilized pre-counting or post-counting to solve this task. This paper takes a detailed look at the memory and speed trade-offs between pre-counting and post-counting strategies for relational learning. A pre-counting approach computes and caches instantiation counts for a large set of relational patterns before model search. A post-counting approach computes an instantiation count dynamically on-demand for each candidate pattern generated during the model search. We describe a novel hybrid approach, tailored to relational data, that achieves a sweet spot with pre-counting for patterns involving positive relationships (e.g. pairs of users who are friends) and post-counting for patterns involving negative relationships (e.g. pairs of users who are not friends). Our hybrid approach scales model discovery to millions of data facts.