Symmetric Collaborative Filtering Using the Noisy Sensor Model

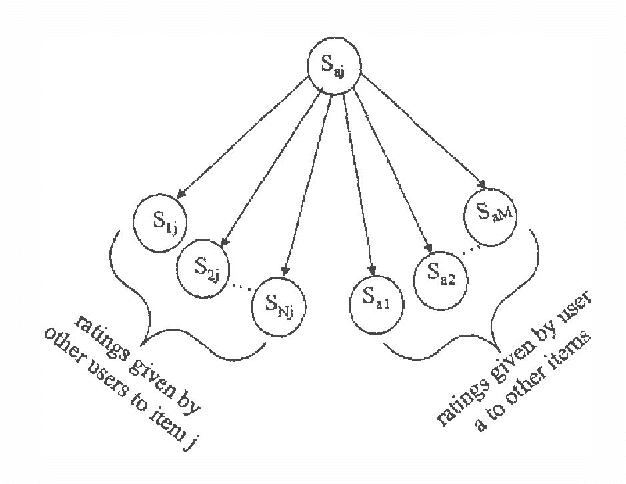
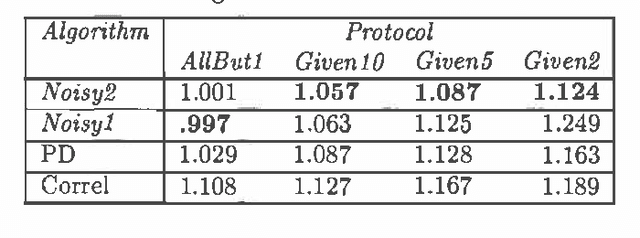
Collaborative filtering is the process of making recommendations regarding the potential preference of a user, for example shopping on the Internet, based on the preference ratings of the user and a number of other users for various items. This paper considers collaborative filtering based on explicitmulti-valued ratings. To evaluate the algorithms, weconsider only {em pure} collaborative filtering, using ratings exclusively, and no other information about the people or items.Our approach is to predict a user's preferences regarding a particularitem by using other people who rated that item and other items ratedby the user as noisy sensors. The noisy sensor model uses Bayes' theorem to compute the probability distribution for the user'srating of a new item. We give two variant models: in one, we learn a{em classical normal linear regression} model of how users rate items; in another,we assume different users rate items the same, but the accuracy of thesensors needs to be learned. We compare these variant models withstate-of-the-art techniques and show how they are significantly better,whether a user has rated only two items or many. We reportempirical results using the EachMovie database footnote{http://research.compaq.com/SRC/eachmovie/} of movie ratings. Wealso show that by considering items similarity along with theusers similarity, the accuracy of the prediction increases.

Efficient Inference in Large Discrete Domains

In this paper we examine the problem of inference in Bayesian Networks with discrete random variables that have very large or even unbounded domains. For example, in a domain where we are trying to identify a person, we may have variables that have as domains, the set of all names, the set of all postal codes, or the set of all credit card numbers. We cannot just have big tables of the conditional probabilities, but need compact representations. We provide an inference algorithm, based on variable elimination, for belief networks containing both large domain and normal discrete random variables. We use intensional (i.e., in terms of procedures) and extensional (in terms of listing the elements) representations of conditional probabilities and of the intermediate factors.