A New Family of Poisson Non-negative Matrix Factorization Methods Using the Shifted Log Link

Poisson non-negative matrix factorization (NMF) is a widely used method to find interpretable "parts-based" decompositions of count data. While many variants of Poisson NMF exist, existing methods assume that the "parts" in the decomposition combine additively. This assumption may be natural in some settings, but not in others. Here we introduce Poisson NMF with the shifted-log link function to relax this assumption. The shifted-log link function has a single tuning parameter, and as this parameter varies the model changes from assuming that parts combine additively (i.e., standard Poisson NMF) to assuming that parts combine more multiplicatively. We provide an algorithm to fit this model by maximum likelihood, and also an approximation that substantially reduces computation time for large, sparse datasets (computations scale with the number of non-zero entries in the data matrix). We illustrate these new methods on a variety of real datasets. Our examples show how the choice of link function in Poisson NMF can substantively impact the results, and how in some settings the use of a shifted-log link function may improve interpretability compared with the standard, additive link.

Gradient-based optimization for variational empirical Bayes multiple regression

Variational empirical Bayes (VEB) methods provide a practically attractive approach to fitting large, sparse, multiple regression models. These methods usually use coordinate ascent to optimize the variational objective function, an approach known as coordinate ascent variational inference (CAVI). Here we propose alternative optimization approaches based on gradient-based (quasi-Newton) methods, which we call gradient-based variational inference (GradVI). GradVI exploits a recent result from Kim et. al. [arXiv:2208.10910] which writes the VEB regression objective function as a penalized regression. Unfortunately the penalty function is not available in closed form, and we present and compare two approaches to dealing with this problem. In simple situations where CAVI performs well, we show that GradVI produces similar predictive performance, and GradVI converges in fewer iterations when the predictors are highly correlated. Furthermore, unlike CAVI, the key computations in GradVI are simple matrix-vector products, and so GradVI is much faster than CAVI in settings where the design matrix admits fast matrix-vector products (e.g., as we show here, trendfiltering applications) and lends itself to parallelized implementations in ways that CAVI does not. GradVI is also very flexible, and could exploit automatic differentiation to easily implement different prior families. Our methods are implemented in an open-source Python software, GradVI (available from https://github.com/stephenslab/gradvi ).

A flexible empirical Bayes approach to multiple linear regression and connections with penalized regression

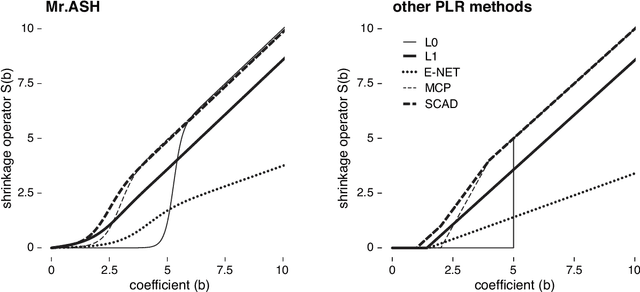
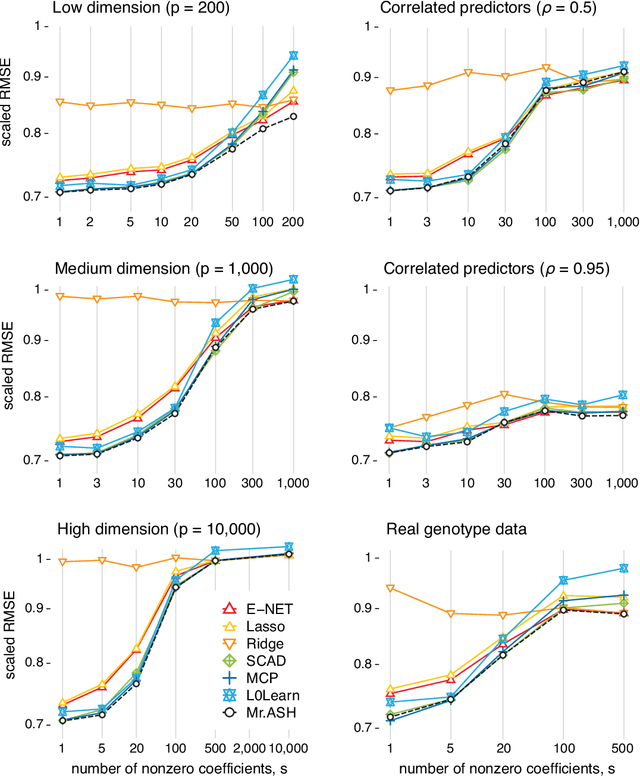
We introduce a new empirical Bayes approach for large-scale multiple linear regression. Our approach combines two key ideas: (i) the use of flexible "adaptive shrinkage" priors, which approximate the nonparametric family of scale mixture of normal distributions by a finite mixture of normal distributions; and (ii) the use of variational approximations to efficiently estimate prior hyperparameters and compute approximate posteriors. Combining these two ideas results in fast and flexible methods, with computational speed comparable to fast penalized regression methods such as the Lasso, and with superior prediction accuracy across a wide range of scenarios. Furthermore, we show that the posterior mean from our method can be interpreted as solving a penalized regression problem, with the precise form of the penalty function being learned from the data by directly solving an optimization problem (rather than being tuned by cross-validation). Our methods are implemented in an R package, mr.ash.alpha, available from https://github.com/stephenslab/mr.ash.alpha

Non-negative matrix factorization algorithms greatly improve topic model fits

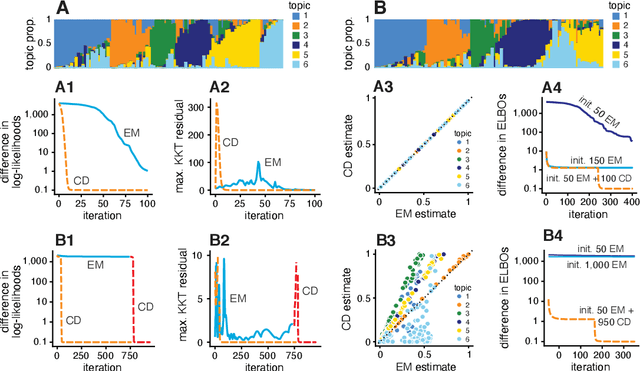
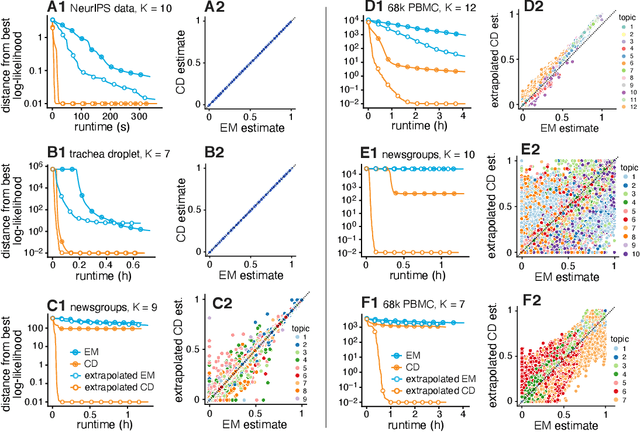
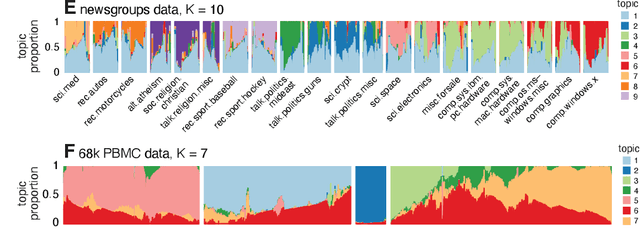
We report on the potential for using algorithms for non-negative matrix factorization (NMF) to improve parameter estimation in topic models. While several papers have studied connections between NMF and topic models, none have suggested leveraging these connections to develop new algorithms for fitting topic models. Importantly, NMF avoids the "sum-to-one" constraints on the topic model parameters, resulting in an optimization problem with simpler structure and more efficient computations. Building on recent advances in optimization algorithms for NMF, we show that first solving the NMF problem then recovering the topic model fit can produce remarkably better fits, and in less time, than standard algorithms for topic models. While we focus primarily on maximum likelihood estimation, we show that this approach also has the potential to improve variational inference for topic models. Our methods are implemented in the R package fastTopics.

Nonparametric Bayesian Logic

The Bayesian Logic (BLOG) language was recently developed for defining first-order probability models over worlds with unknown numbers of objects. It handles important problems in AI, including data association and population estimation. This paper extends BLOG by adopting generative processes over function spaces - known as nonparametrics in the Bayesian literature. We introduce syntax for reasoning about arbitrary collections of objects, and their properties, in an intuitive manner. By exploiting exchangeability, distributions over unknown objects and their attributes are cast as Dirichlet processes, which resolve difficulties in model selection and inference caused by varying numbers of objects. We demonstrate these concepts with application to citation matching.