Non-negative matrix factorization algorithms greatly improve topic model fits
Paper and Code
May 27, 2021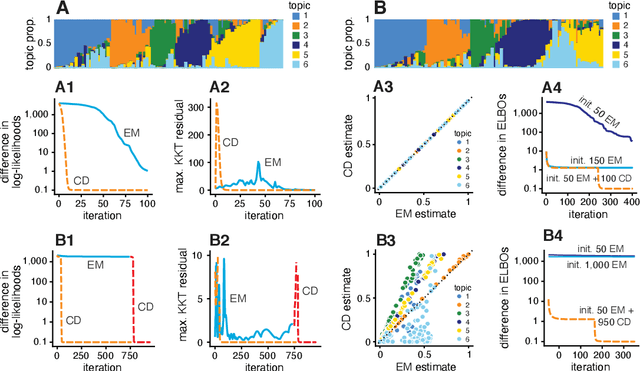
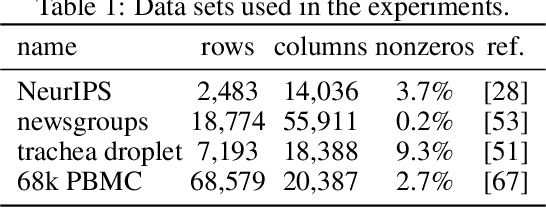
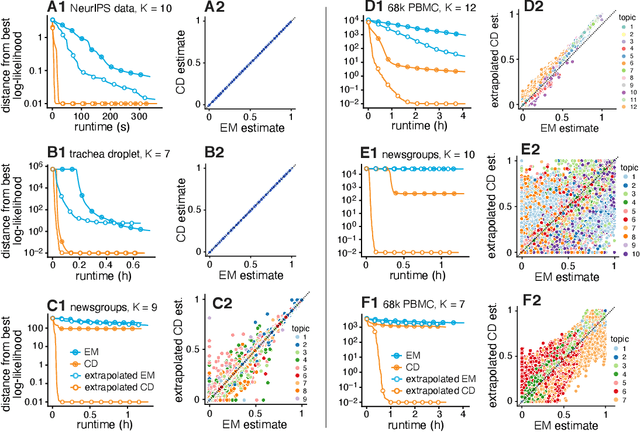
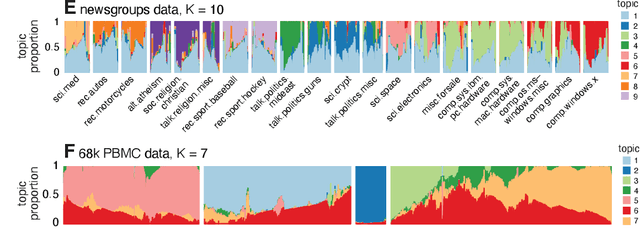
We report on the potential for using algorithms for non-negative matrix factorization (NMF) to improve parameter estimation in topic models. While several papers have studied connections between NMF and topic models, none have suggested leveraging these connections to develop new algorithms for fitting topic models. Importantly, NMF avoids the "sum-to-one" constraints on the topic model parameters, resulting in an optimization problem with simpler structure and more efficient computations. Building on recent advances in optimization algorithms for NMF, we show that first solving the NMF problem then recovering the topic model fit can produce remarkably better fits, and in less time, than standard algorithms for topic models. While we focus primarily on maximum likelihood estimation, we show that this approach also has the potential to improve variational inference for topic models. Our methods are implemented in the R package fastTopics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge