Gradient-based optimization for variational empirical Bayes multiple regression

Variational empirical Bayes (VEB) methods provide a practically attractive approach to fitting large, sparse, multiple regression models. These methods usually use coordinate ascent to optimize the variational objective function, an approach known as coordinate ascent variational inference (CAVI). Here we propose alternative optimization approaches based on gradient-based (quasi-Newton) methods, which we call gradient-based variational inference (GradVI). GradVI exploits a recent result from Kim et. al. [arXiv:2208.10910] which writes the VEB regression objective function as a penalized regression. Unfortunately the penalty function is not available in closed form, and we present and compare two approaches to dealing with this problem. In simple situations where CAVI performs well, we show that GradVI produces similar predictive performance, and GradVI converges in fewer iterations when the predictors are highly correlated. Furthermore, unlike CAVI, the key computations in GradVI are simple matrix-vector products, and so GradVI is much faster than CAVI in settings where the design matrix admits fast matrix-vector products (e.g., as we show here, trendfiltering applications) and lends itself to parallelized implementations in ways that CAVI does not. GradVI is also very flexible, and could exploit automatic differentiation to easily implement different prior families. Our methods are implemented in an open-source Python software, GradVI (available from https://github.com/stephenslab/gradvi ).

Empirical Bayes Covariance Decomposition, and a solution to the Multiple Tuning Problem in Sparse PCA

Sparse Principal Components Analysis (PCA) has been proposed as a way to improve both interpretability and reliability of PCA. However, use of sparse PCA in practice is hindered by the difficulty of tuning the multiple hyperparameters that control the sparsity of different PCs (the "multiple tuning problem", MTP). Here we present a solution to the MTP using Empirical Bayes methods. We first introduce a general formulation for penalized PCA of a data matrix $\mathbf{X}$, which includes some existing sparse PCA methods as special cases. We show that this formulation also leads to a penalized decomposition of the covariance (or Gram) matrix, $\mathbf{X}^T\mathbf{X}$. We introduce empirical Bayes versions of these penalized problems, in which the penalties are determined by prior distributions that are estimated from the data by maximum likelihood rather than cross-validation. The resulting "Empirical Bayes Covariance Decomposition" provides a principled and efficient solution to the MTP in sparse PCA, and one that can be immediately extended to incorporate other structural assumptions (e.g. non-negative PCA). We illustrate the effectiveness of this approach on both simulated and real data examples.

A flexible empirical Bayes approach to multiple linear regression and connections with penalized regression

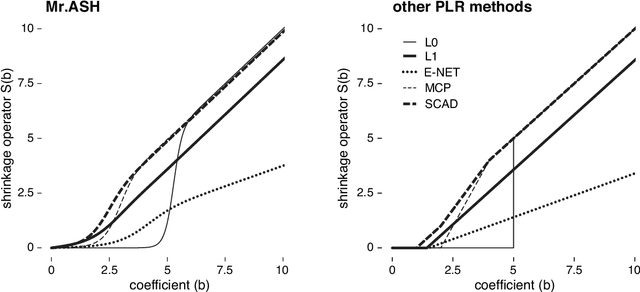
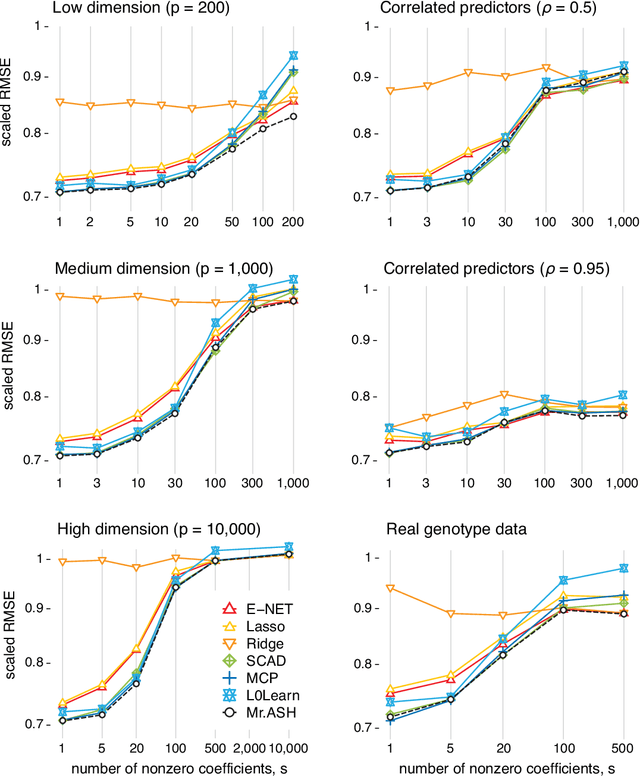
We introduce a new empirical Bayes approach for large-scale multiple linear regression. Our approach combines two key ideas: (i) the use of flexible "adaptive shrinkage" priors, which approximate the nonparametric family of scale mixture of normal distributions by a finite mixture of normal distributions; and (ii) the use of variational approximations to efficiently estimate prior hyperparameters and compute approximate posteriors. Combining these two ideas results in fast and flexible methods, with computational speed comparable to fast penalized regression methods such as the Lasso, and with superior prediction accuracy across a wide range of scenarios. Furthermore, we show that the posterior mean from our method can be interpreted as solving a penalized regression problem, with the precise form of the penalty function being learned from the data by directly solving an optimization problem (rather than being tuned by cross-validation). Our methods are implemented in an R package, mr.ash.alpha, available from https://github.com/stephenslab/mr.ash.alpha

Non-negative matrix factorization algorithms greatly improve topic model fits

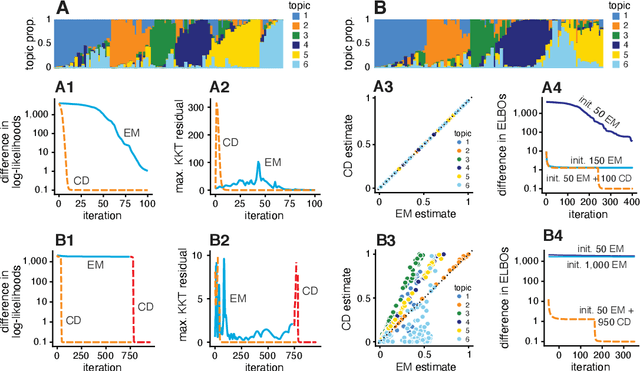
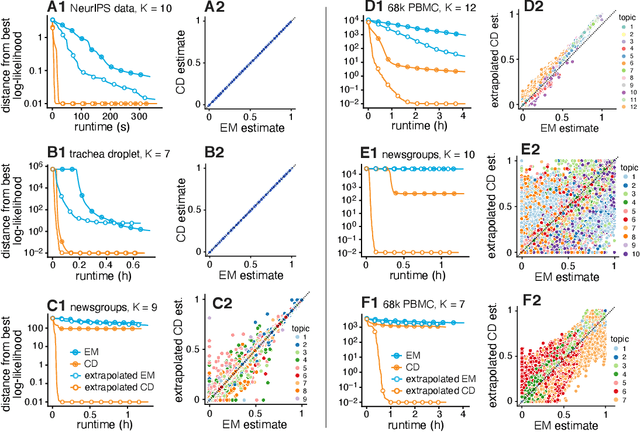
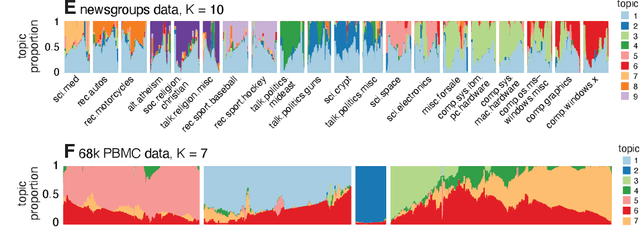
We report on the potential for using algorithms for non-negative matrix factorization (NMF) to improve parameter estimation in topic models. While several papers have studied connections between NMF and topic models, none have suggested leveraging these connections to develop new algorithms for fitting topic models. Importantly, NMF avoids the "sum-to-one" constraints on the topic model parameters, resulting in an optimization problem with simpler structure and more efficient computations. Building on recent advances in optimization algorithms for NMF, we show that first solving the NMF problem then recovering the topic model fit can produce remarkably better fits, and in less time, than standard algorithms for topic models. While we focus primarily on maximum likelihood estimation, we show that this approach also has the potential to improve variational inference for topic models. Our methods are implemented in the R package fastTopics.

Solving the Empirical Bayes Normal Means Problem with Correlated Noise

The Normal Means problem plays a fundamental role in many areas of modern high-dimensional statistics, both in theory and practice. And the Empirical Bayes (EB) approach to solving this problem has been shown to be highly effective, again both in theory and practice. However, almost all EB treatments of the Normal Means problem assume that the observations are independent. In practice correlations are ubiquitous in real-world applications, and these correlations can grossly distort EB estimates. Here, exploiting theory from Schwartzman (2010), we develop new EB methods for solving the Normal Means problem that take account of unknown correlations among observations. We provide practical software implementations of these methods, and illustrate them in the context of large-scale multiple testing problems and False Discovery Rate (FDR) control. In realistic numerical experiments our methods compare favorably with other commonly-used multiple testing methods.