Michael P. Beddoes
Can Uncertainty Management be Realized in a Finite Totally Ordered Probability Algebra?
Mar 27, 2013Abstract:In this paper, the feasibility of using finite totally ordered probability models under Alelinnas's Theory of Probabilistic Logic [Aleliunas, 1988] is investigated. The general form of the probability algebra of these models is derived and the number of possible algebras with given size is deduced. Based on this analysis, we discuss problems of denominator-indifference and ambiguity-generation that arise in reasoning by cases and abductive reasoning. An example is given that illustrates how these problems arise. The investigation shows that a finite probability model may be of very limited usage.
Exploring Localization in Bayesian Networks for Large Expert Systems
Mar 13, 2013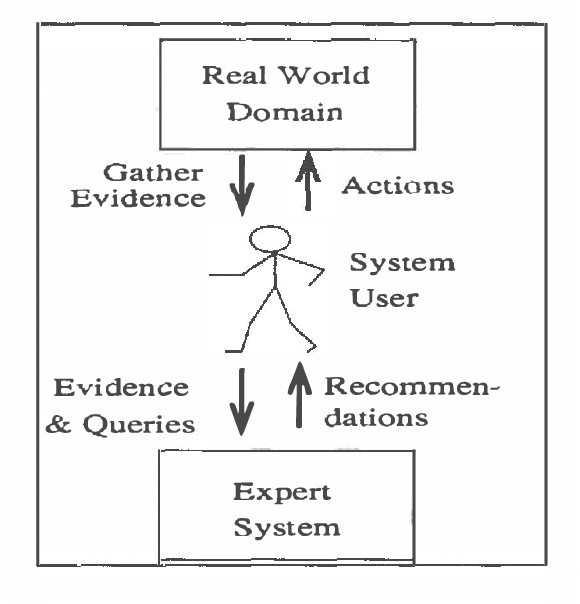
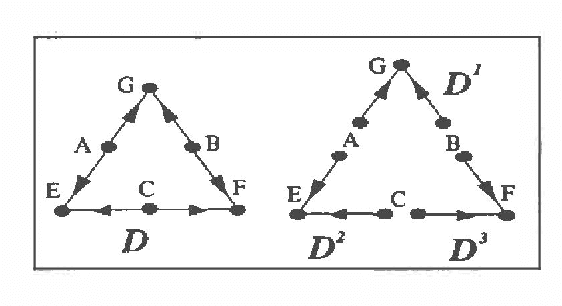
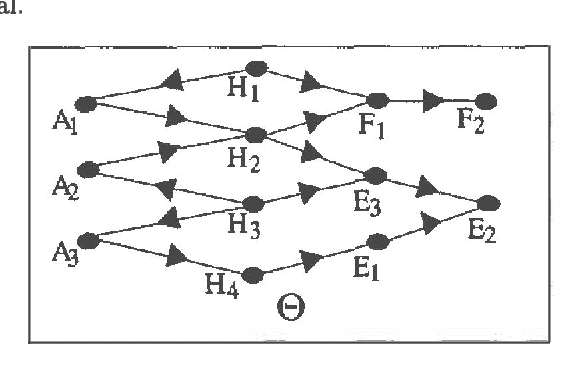
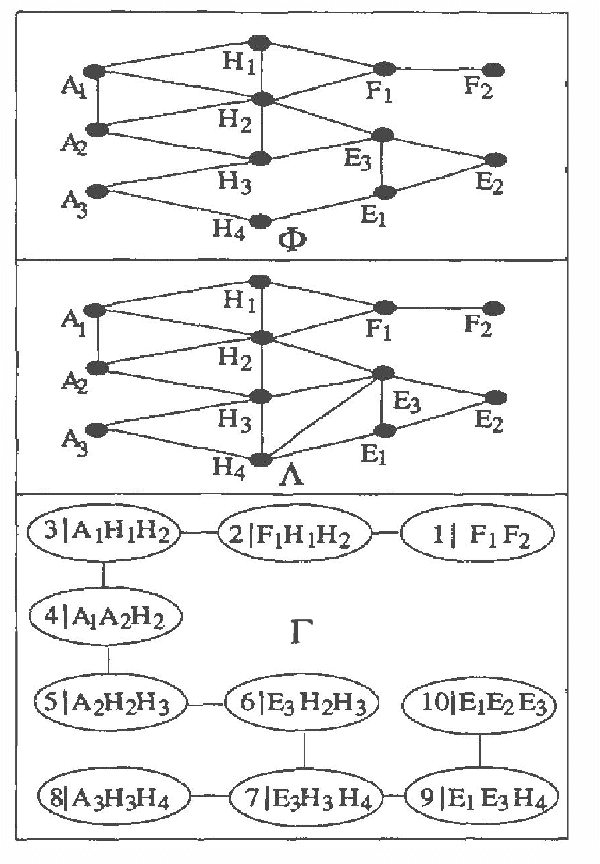
Abstract:Current Bayesian net representations do not consider structure in the domain and include all variables in a homogeneous network. At any time, a human reasoner in a large domain may direct his attention to only one of a number of natural subdomains, i.e., there is ?localization' of queries and evidence. In such a case, propagating evidence through a homogeneous network is inefficient since the entire network has to be updated each time. This paper presents multiply sectioned Bayesian networks that enable a (localization preserving) representation of natural subdomains by separate Bayesian subnets. The subnets are transformed into a set of permanent junction trees such that evidential reasoning takes place at only one of them at a time. Probabilities obtained are identical to those that would be obtained from the homogeneous network. We discuss attention shift to a different junction tree and propagation of previously acquired evidence. Although the overall system can be large, computational requirements are governed by the size of only one junction tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge