High Level Path Planning with Uncertainty

For high level path planning, environments are usually modeled as distance graphs, and path planning problems are reduced to computing the shortest path in distance graphs. One major drawback of this modeling is the inability to model uncertainties, which are often encountered in practice. In this paper, a new tool, called U-yraph, is proposed for environment modeling. A U-graph is an extension of distance graphs with the ability to handle a kind of uncertainty. By modeling an uncertain environment as a U-graph, and a navigation problem as a Markovian decision process, we can precisely define a new optimality criterion for navigation plans, and more importantly, we can come up with a general algorithm for computing optimal plans for navigation tasks.

Incremental computation of the value of perfect information in stepwise-decomposable influence diagrams

To determine the value of perfect information in an influence diagram, one needs first to modify the diagram to reflect the change in information availability, and then to compute the optimal expected values of both the original diagram and the modified diagram. The value of perfect information is the difference between the two optimal expected values. This paper is about how to speed up the computation of the optimal expected value of the modified diagram by making use of the intermediate computation results obtained when computing the optimal expected value of the original diagram.

Solving Asymmetric Decision Problems with Influence Diagrams

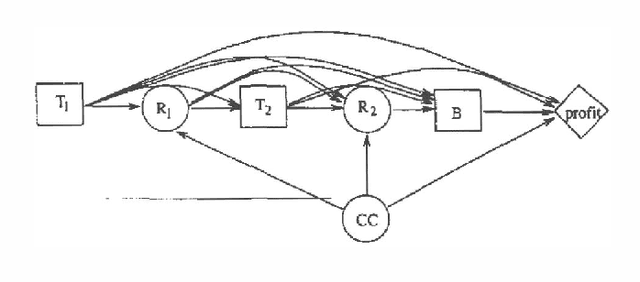
While influence diagrams have many advantages as a representation framework for Bayesian decision problems, they have a serious drawback in handling asymmetric decision problems. To be represented in an influence diagram, an asymmetric decision problem must be symmetrized. A considerable amount of unnecessary computation may be involved when a symmetrized influence diagram is evaluated by conventional algorithms. In this paper we present an approach for avoiding such unnecessary computation in influence diagram evaluation.