Incremental Pruning: A Simple, Fast, Exact Method for Partially Observable Markov Decision Processes
Paper and Code
Feb 06, 2013

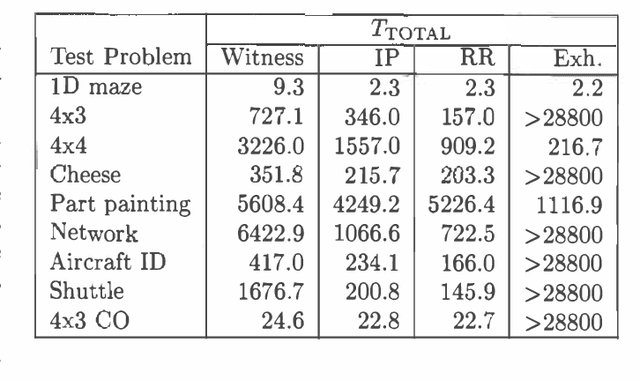

Most exact algorithms for general partially observable Markov decision processes (POMDPs) use a form of dynamic programming in which a piecewise-linear and convex representation of one value function is transformed into another. We examine variations of the "incremental pruning" method for solving this problem and compare them to earlier algorithms from theoretical and empirical perspectives. We find that incremental pruning is presently the most efficient exact method for solving POMDPs.
* Appears in Proceedings of the Thirteenth Conference on Uncertainty in
Artificial Intelligence (UAI1997)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge