Guillaume Infantes
Earth Observation Satellite Scheduling with Graph Neural Networks
Aug 27, 2024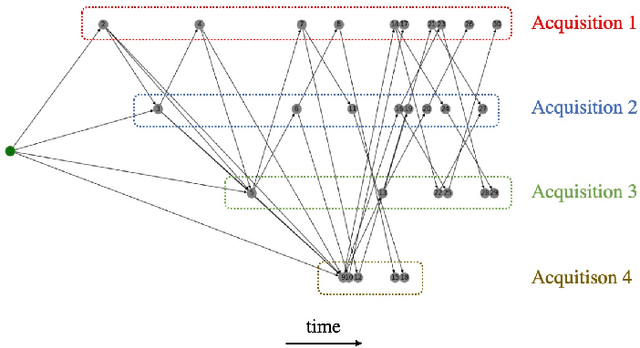
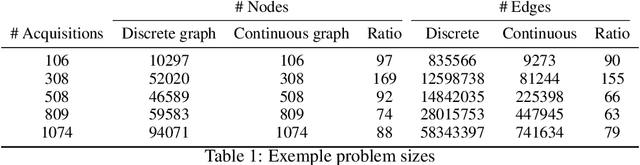
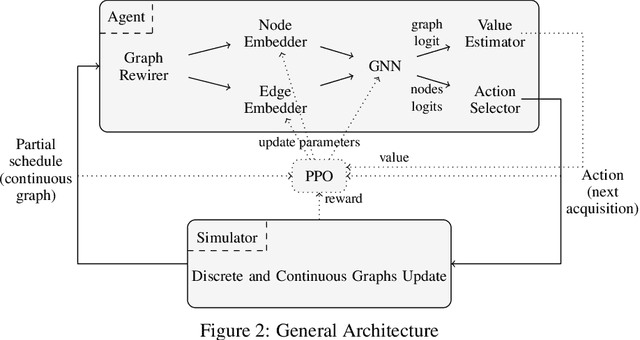
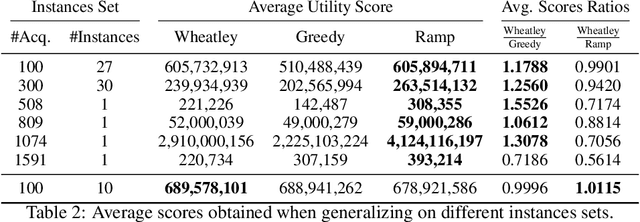
Abstract:The Earth Observation Satellite Planning (EOSP) is a difficult optimization problem with considerable practical interest. A set of requested observations must be scheduled on an agile Earth observation satellite while respecting constraints on their visibility window, as well as maneuver constraints that impose varying delays between successive observations. In addition, the problem is largely oversubscribed: there are much more candidate observations than what can possibly be achieved. Therefore, one must select the set of observations that will be performed while maximizing their weighted cumulative benefit, and propose a feasible schedule for these observations. As previous work mostly focused on heuristic and iterative search algorithms, this paper presents a new technique for selecting and scheduling observations based on Graph Neural Networks (GNNs) and Deep Reinforcement Learning (DRL). GNNs are used to extract relevant information from the graphs representing instances of the EOSP, and DRL drives the search for optimal schedules. Our simulations show that it is able to learn on small problem instances and generalize to larger real-world instances, with very competitive performance compared to traditional approaches.
Open Loop Execution of Tree-Search Algorithms
May 03, 2018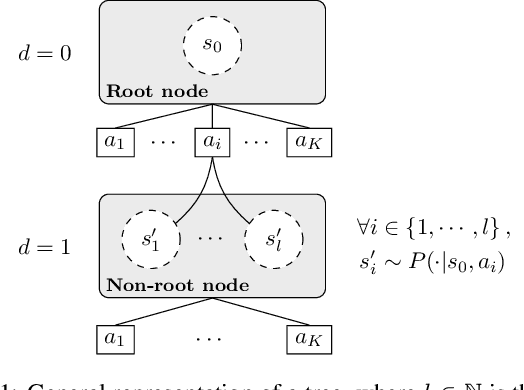
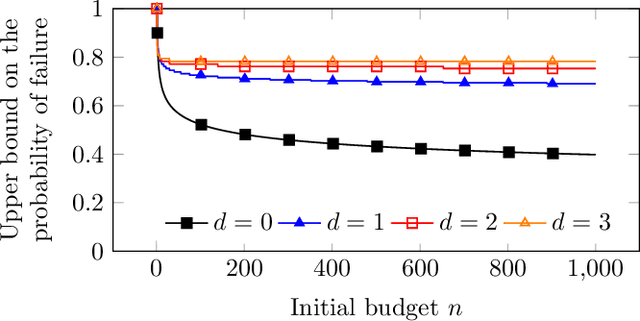
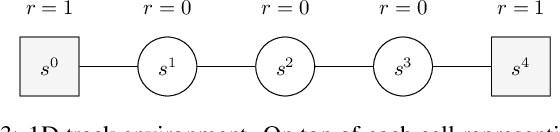
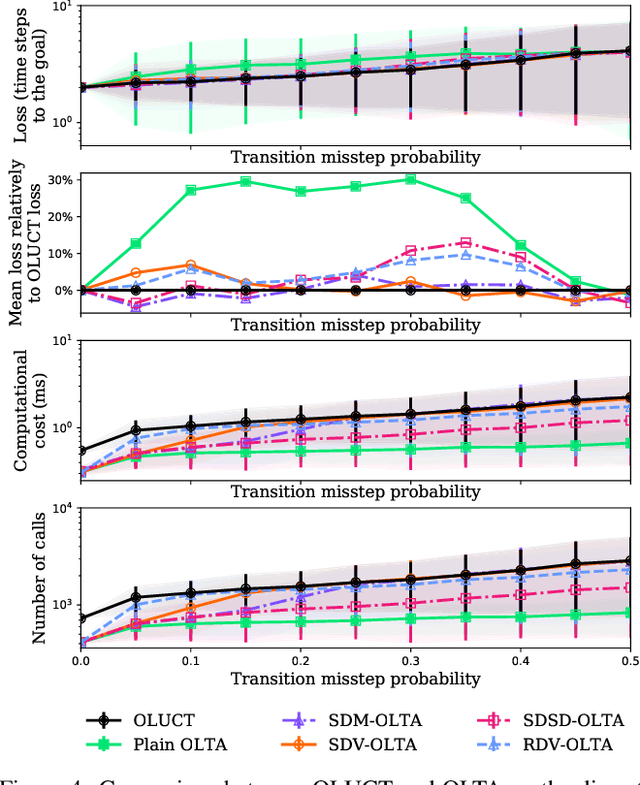
Abstract:In the context of tree-search stochastic planning algorithms where a generative model is available, we consider on-line planning algorithms building trees in order to recommend an action. We investigate the question of avoiding re-planning in subsequent decision steps by directly using sub-trees as action recommender. Firstly, we propose a method for open loop control via a new algorithm taking the decision of re-planning or not at each time step based on an analysis of the statistics of the sub-tree. Secondly, we show that the probability of selecting a suboptimal action at any depth of the tree can be upper bounded and converges towards zero. Moreover, this upper bound decays in a logarithmic way between subsequent depths. This leads to a distinction between node-wise optimality and state-wise optimality. Finally, we empirically demonstrate that our method achieves a compromise between loss of performance and computational gain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge