Optimal Limited Contingency Planning

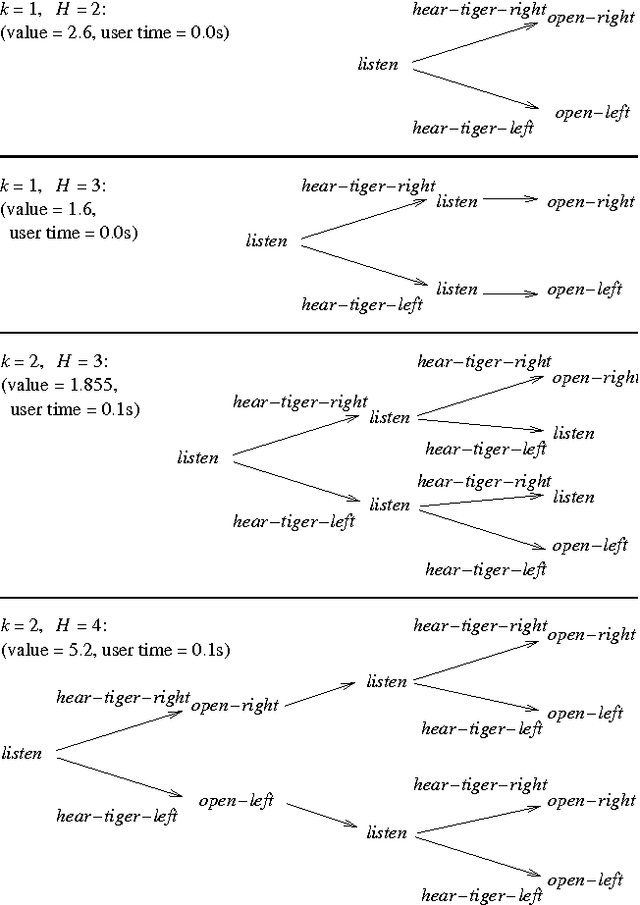
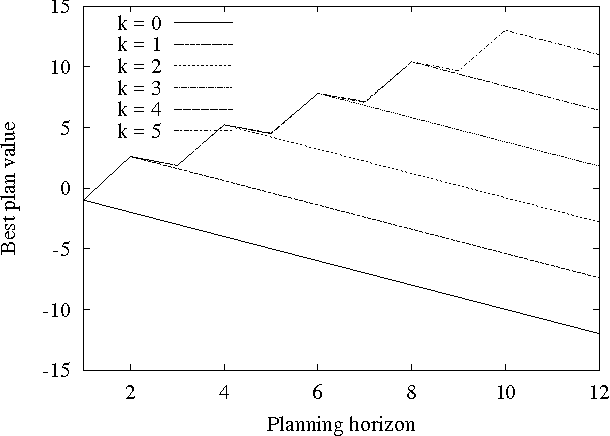
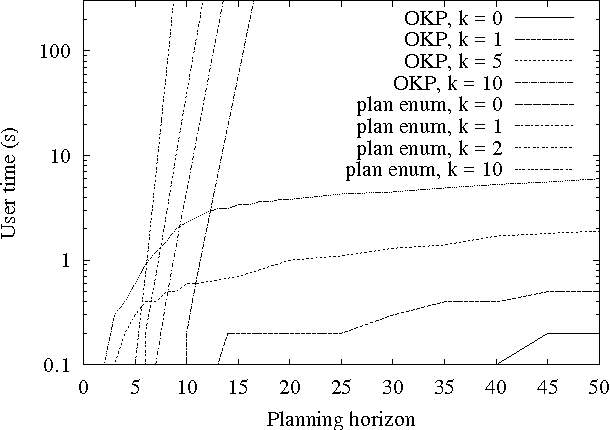
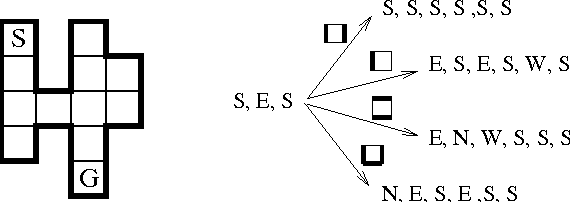
For a given problem, the optimal Markov policy can be considerred as a conditional or contingent plan containing a (potentially large) number of branches. Unfortunately, there are applications where it is desirable to strictly limit the number of decision points and branches in a plan. For example, it may be that plans must later undergo more detailed simulation to verify correctness and safety, or that they must be simple enough to be understood and analyzed by humans. As a result, it may be necessary to limit consideration to plans with only a small number of branches. This raises the question of how one goes about finding optimal plans containing only a limited number of branches. In this paper, we present an any-time algorithm for optimal k-contingency planning (OKP). It is the first optimal algorithm for limited contingency planning that is not an explicit enumeration of possible contingent plans. By modelling the problem as a Partially Observable Markov Decision Process, it implements the Bellman optimality principle and prunes the solution space. We present experimental results of applying this algorithm to some simple test cases.