Muhammad Asif Rana
Geometric Fabrics: Generalizing Classical Mechanics to Capture the Physics of Behavior
Sep 21, 2021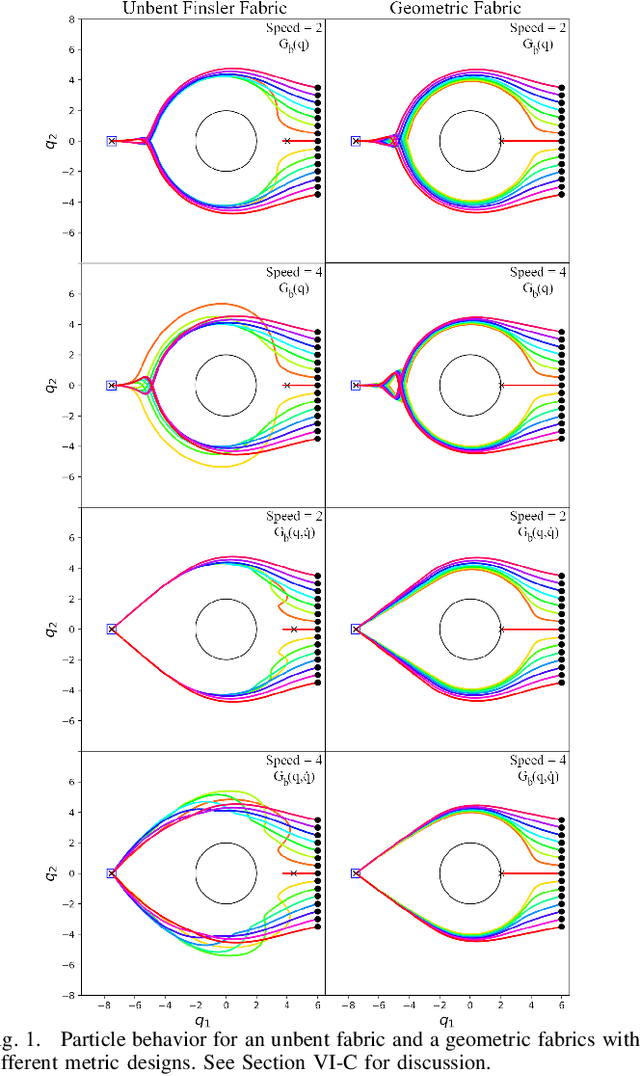
Abstract:Classical mechanical systems are central to controller design in energy shaping methods of geometric control. However, their expressivity is limited by position-only metrics and the intimate link between metric and geometry. Recent work on Riemannian Motion Policies (RMPs) has shown that shedding these restrictions results in powerful design tools, but at the expense of theoretical guarantees. In this work, we generalize classical mechanics to what we call geometric fabrics, whose expressivity and theory enable the design of systems that outperform RMPs in practice. Geometric fabrics strictly generalize classical mechanics forming a new physics of behavior by first generalizing them to Finsler geometries and then explicitly bending them to shape their behavior. We develop the theory of fabrics and present both a collection of controlled experiments examining their theoretical properties and a set of robot system experiments showing improved performance over a well-engineered and hardened implementation of RMPs, our current state-of-the-art in controller design.
Geometric Fabrics for the Acceleration-based Design of Robotic Motion
Nov 11, 2020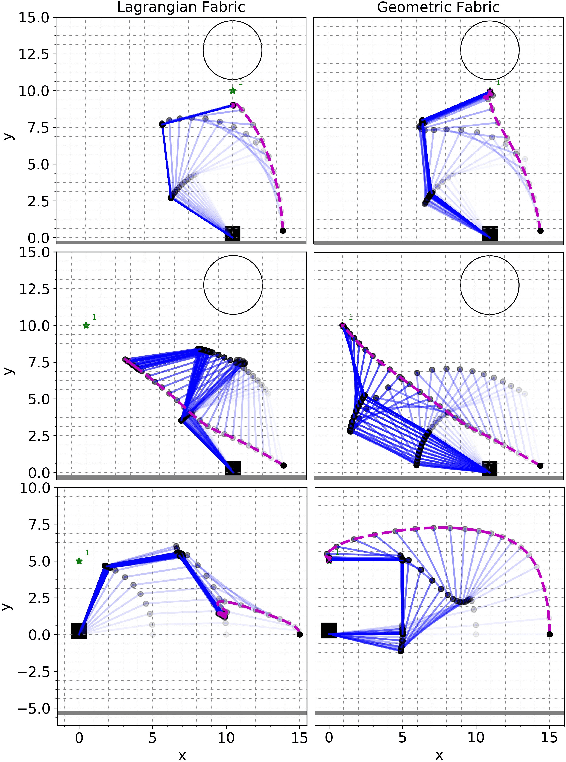

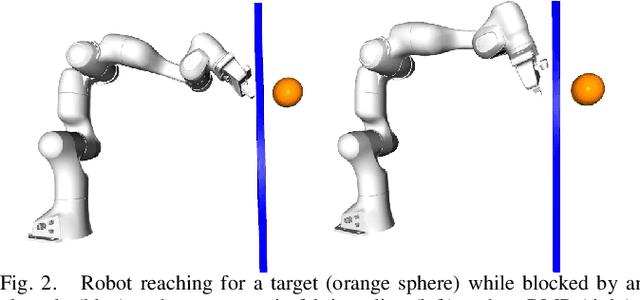
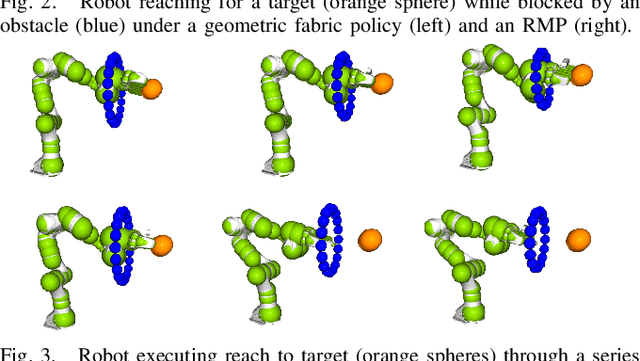
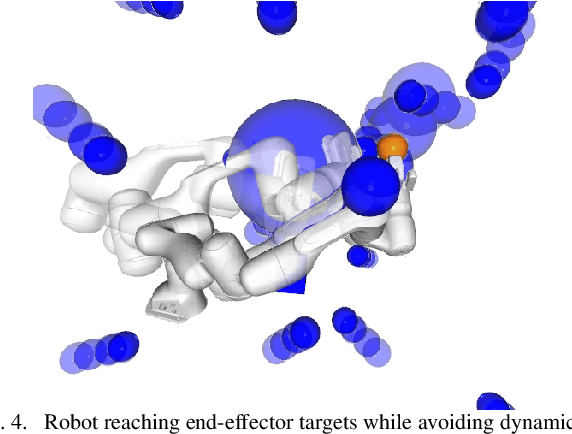
Abstract:This paper describes the pragmatic design and construction of geometric fabrics for shaping a robot's task-independent nominal behavior, capturing behavioral components such as obstacle avoidance, joint limit avoidance, redundancy resolution, global navigation heuristics, etc. Geometric fabrics constitute the most concrete incarnation of a new mathematical formulation for reactive behavior called optimization fabrics. Fabrics generalize recent work on Riemannian Motion Policies (RMPs); they add provable stability guarantees and improve design consistency while promoting the intuitive acceleration-based principles of modular design that make RMPs successful. We describe a suite of mathematical modeling tools that practitioners can employ in practice and demonstrate both how to mitigate system complexity by constructing behaviors layer-wise and how to employ these tools to design robust, strongly-generalizing, policies that solve practical problems one would expect to find in industry applications. Our system exhibits intelligent global navigation behaviors expressed entirely as fabrics with zero planning or state machine governance.
Optimization Fabrics
Aug 22, 2020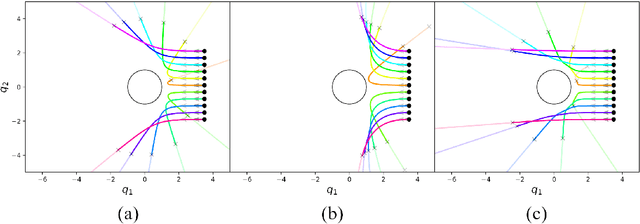
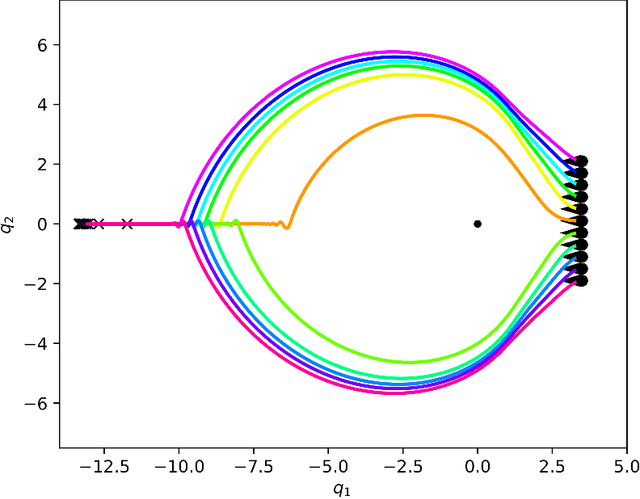
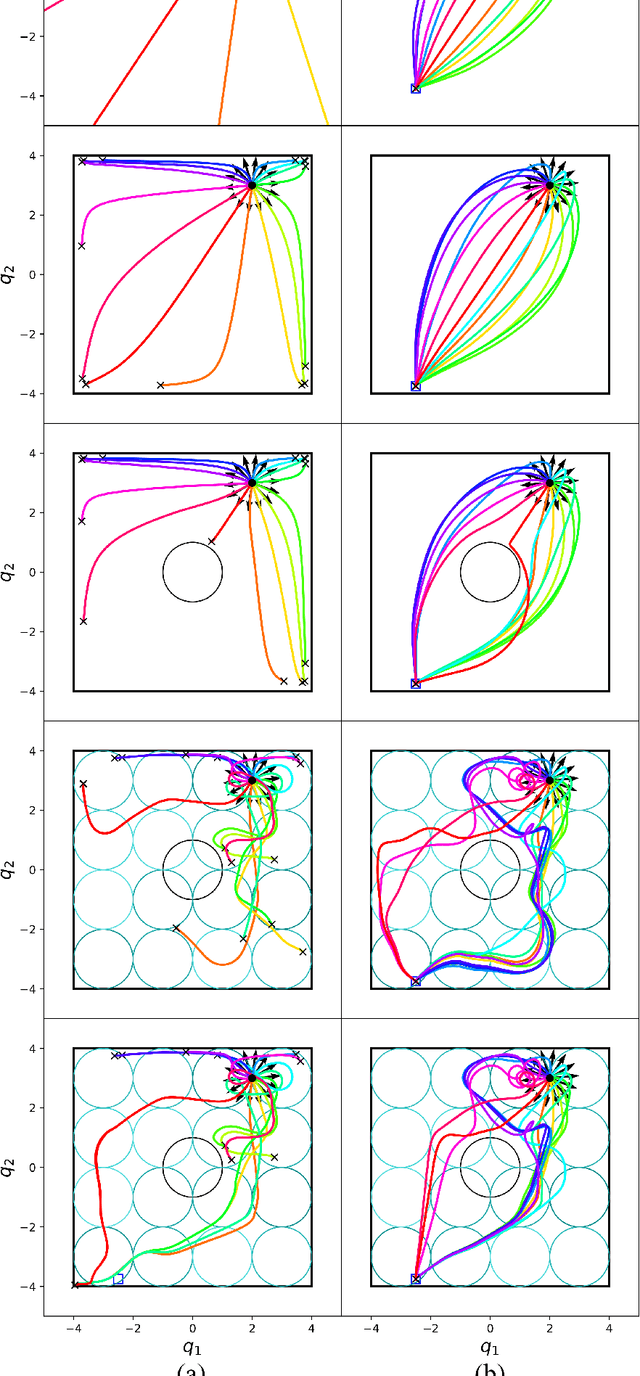
Abstract:This paper presents a theory of optimization fabrics, second-order differential equations that encode nominal behaviors on a space and can be used to define the behavior of a smooth optimizer. Optimization fabrics can encode commonalities among optimization problems that reflect the structure of the space itself, enabling smooth optimization processes to intelligently navigate each problem even when optimizing simple naive potential functions. Importantly, optimization over a fabric is inherently asymptotically stable. The majority of this paper is dedicated to the development of a tool set for the design and use of a broad class of fabrics called geometric fabrics. Geometric fabrics encode behavior as general nonlinear geometries which are covariant second-order differential equations with a special homogeneity property that ensures their behavior is independent of the system's speed through the medium. A class of Finsler Lagrangian energies can be used to both define how these nonlinear geometries combine with one another and how they react when potential functions force them from their nominal paths. Furthermore, these geometric fabrics are closed under the standard operations of pullback and combination on a transform tree. For behavior representation, this class of geometric fabrics constitutes a broad class of spectral semi-sprays (specs), also known as Riemannian Motion Policies (RMPs) in the context of robotic motion generation, that captures both the intuitive separation between acceleration policy and priority metric critical for modular design and are inherently stable. Therefore, geometric fabrics are safe and easier to use by less experienced behavioral designers. Application of this theory to policy representation and generalization in learning are discussed as well.
Euclideanizing Flows: Diffeomorphic Reduction for Learning Stable Dynamical Systems
May 27, 2020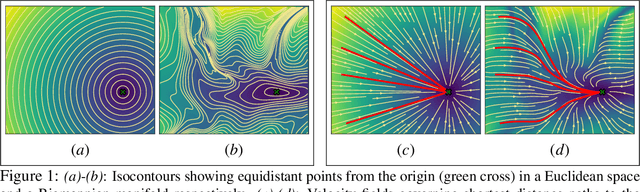
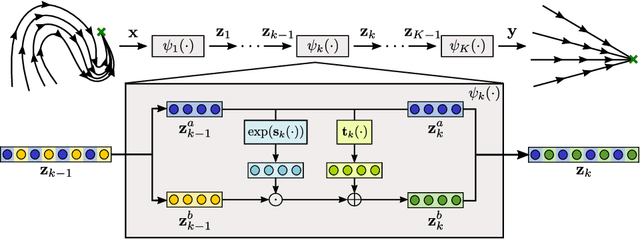
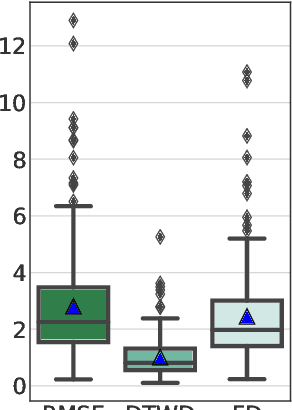
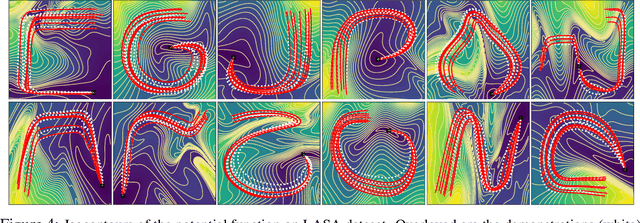
Abstract:Robotic tasks often require motions with complex geometric structures. We present an approach to learn such motions from a limited number of human demonstrations by exploiting the regularity properties of human motions e.g. stability, smoothness, and boundedness. The complex motions are encoded as rollouts of a stable dynamical system, which, under a change of coordinates defined by a diffeomorphism, is equivalent to a simple, hand-specified dynamical system. As an immediate result of using diffeomorphisms, the stability property of the hand-specified dynamical system directly carry over to the learned dynamical system. Inspired by recent works in density estimation, we propose to represent the diffeomorphism as a composition of simple parameterized diffeomorphisms. Additional structure is imposed to provide guarantees on the smoothness of the generated motions. The efficacy of this approach is demonstrated through validation on an established benchmark as well demonstrations collected on a real-world robotic system.
Taking Recoveries to Task: Recovery-Driven Development for Recipe-based Robot Tasks
Jan 28, 2020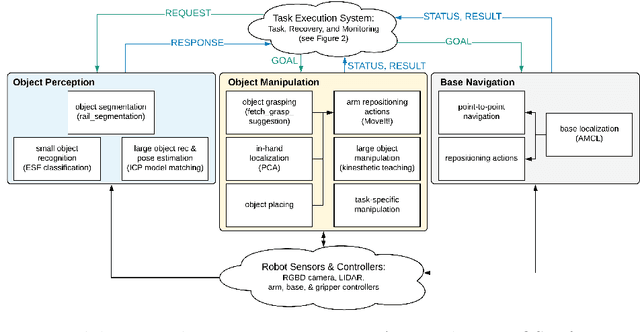
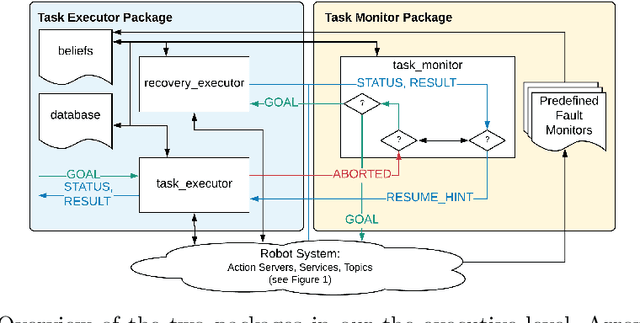

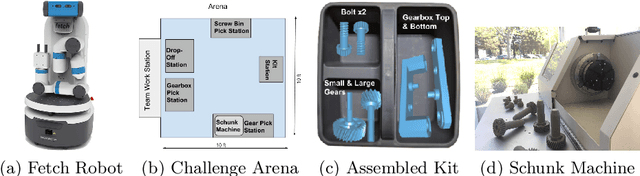
Abstract:Robot task execution when situated in real-world environments is fragile. As such, robot architectures must rely on robust error recovery, adding non-trivial complexity to highly-complex robot systems. To handle this complexity in development, we introduce Recovery-Driven Development (RDD), an iterative task scripting process that facilitates rapid task and recovery development by leveraging hierarchical specification, separation of nominal task and recovery development, and situated testing. We validate our approach with our challenge-winning mobile manipulator software architecture developed using RDD for the FetchIt! Challenge at the IEEE 2019 International Conference on Robotics and Automation. We attribute the success of our system to the level of robustness achieved using RDD, and conclude with lessons learned for developing such systems.
Learning Generalizable Robot Skills from Demonstrations in Cluttered Environments
Aug 04, 2018
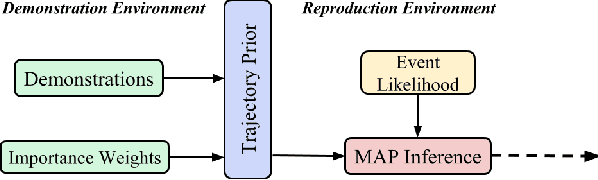
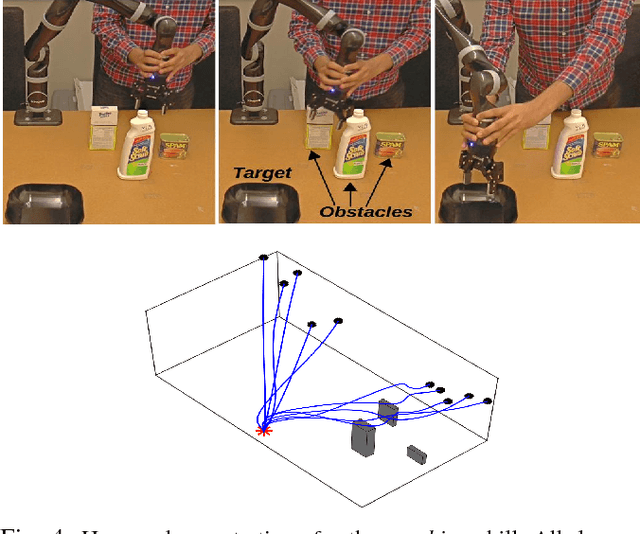
Abstract:Learning from Demonstration (LfD) is a popular approach to endowing robots with skills without having to program them by hand. Typically, LfD relies on human demonstrations in clutter-free environments. This prevents the demonstrations from being affected by irrelevant objects, whose influence can obfuscate the true intention of the human or the constraints of the desired skill. However, it is unrealistic to assume that the robot's environment can always be restructured to remove clutter when capturing human demonstrations. To contend with this problem, we develop an importance weighted batch and incremental skill learning approach, building on a recent inference-based technique for skill representation and reproduction. Our approach reduces unwanted environmental influences on the learned skill, while still capturing the salient human behavior. We provide both batch and incremental versions of our approach and validate our algorithms on a 7-DOF JACO2 manipulator with reaching and placing skills.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge