Geometric Fabrics for the Acceleration-based Design of Robotic Motion

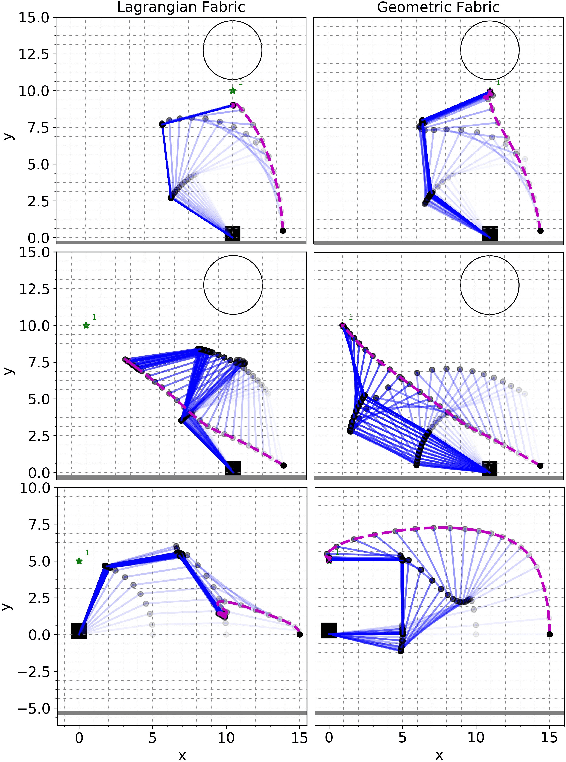
This paper describes the pragmatic design and construction of geometric fabrics for shaping a robot's task-independent nominal behavior, capturing behavioral components such as obstacle avoidance, joint limit avoidance, redundancy resolution, global navigation heuristics, etc. Geometric fabrics constitute the most concrete incarnation of a new mathematical formulation for reactive behavior called optimization fabrics. Fabrics generalize recent work on Riemannian Motion Policies (RMPs); they add provable stability guarantees and improve design consistency while promoting the intuitive acceleration-based principles of modular design that make RMPs successful. We describe a suite of mathematical modeling tools that practitioners can employ in practice and demonstrate both how to mitigate system complexity by constructing behaviors layer-wise and how to employ these tools to design robust, strongly-generalizing, policies that solve practical problems one would expect to find in industry applications. Our system exhibits intelligent global navigation behaviors expressed entirely as fabrics with zero planning or state machine governance.