Mandy Xie
On the Utility of Koopman Operator Theory in Learning Dexterous Manipulation Skills
Mar 23, 2023Abstract:Recent advances in learning-based approaches have led to impressive dexterous manipulation capabilities. Yet, we haven't witnessed widespread adoption of these capabilities beyond the laboratory. This is likely due to practical limitations, such as significant computational burden, inscrutable policy architectures, sensitivity to parameter initializations, and the considerable technical expertise required for implementation. In this work, we investigate the utility of Koopman operator theory in alleviating these limitations. Koopman operators are simple yet powerful control-theoretic structures that help represent complex nonlinear dynamics as linear systems in higher-dimensional spaces. Motivated by the fact that complex nonlinear dynamics underlie dexterous manipulation, we develop an imitation learning framework that leverages Koopman operators to simultaneously learn the desired behavior of both robot and object states. We demonstrate that a Koopman operator-based framework is surprisingly effective for dexterous manipulation and offers a number of unique benefits. First, the learning process is analytical, eliminating the sensitivity to parameter initializations and painstaking hyperparameter optimization. Second, the learned reference dynamics can be combined with a task-agnostic tracking controller such that task changes and variations can be handled with ease. Third, a Koopman operator-based approach can perform comparably to state-of-the-art imitation learning algorithms in terms of task success rate and imitation error, while being an order of magnitude more computationally efficient. In addition, we discuss a number of avenues for future research made available by this work.
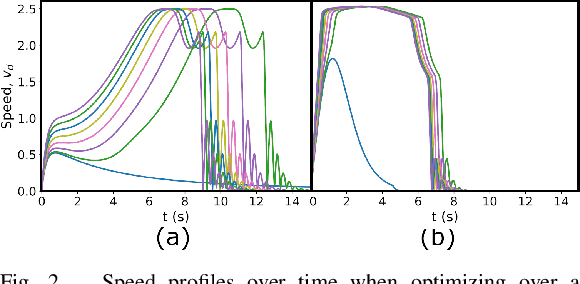
Geometric Fabrics: Generalizing Classical Mechanics to Capture the Physics of Behavior
Sep 21, 2021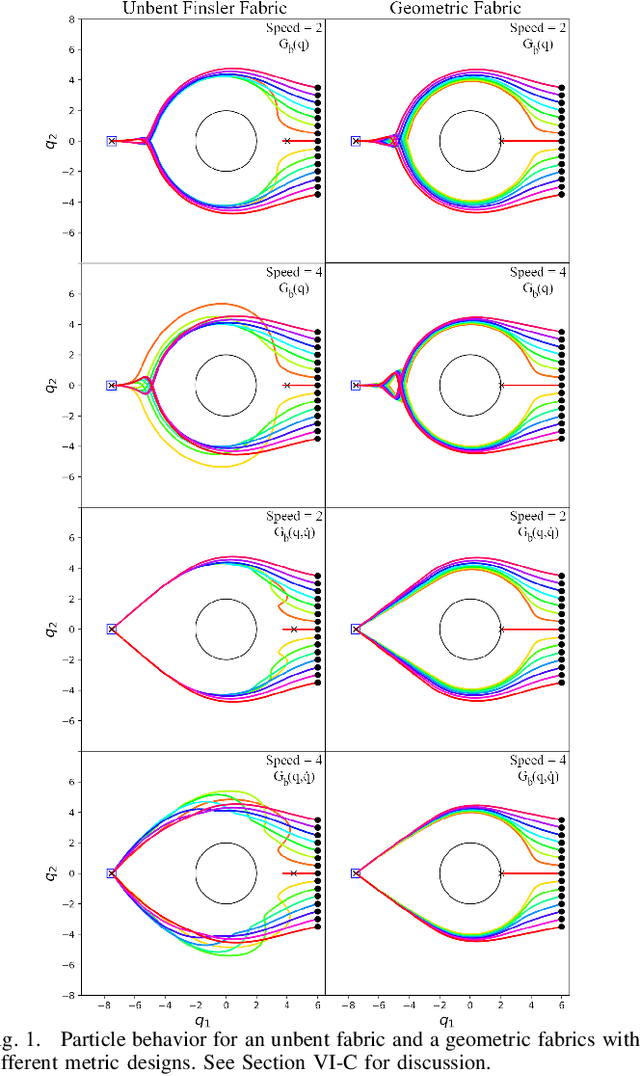
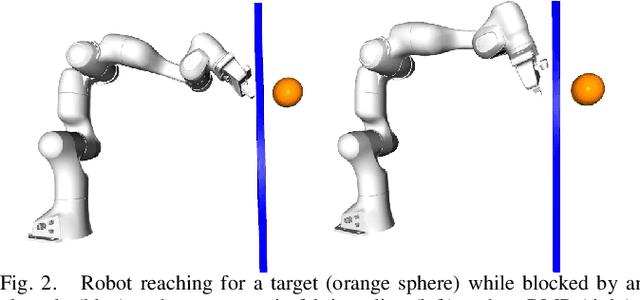
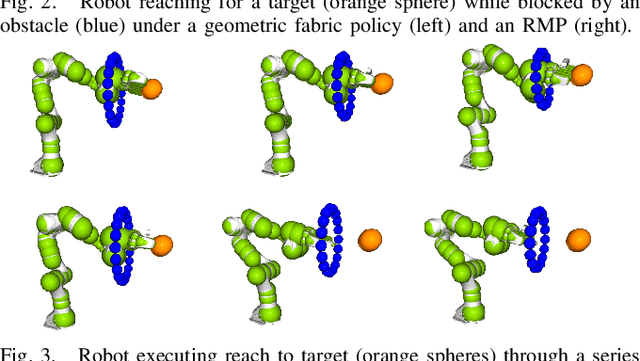
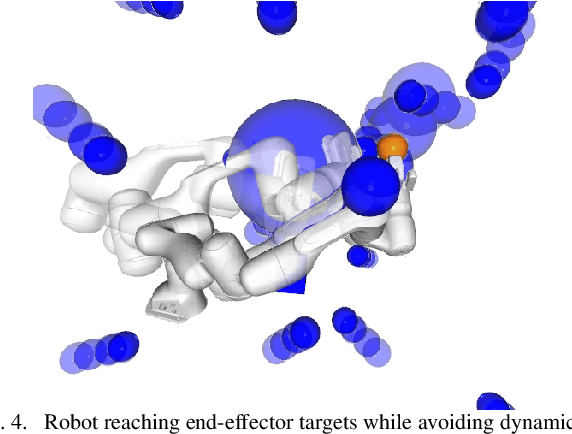
Abstract:Classical mechanical systems are central to controller design in energy shaping methods of geometric control. However, their expressivity is limited by position-only metrics and the intimate link between metric and geometry. Recent work on Riemannian Motion Policies (RMPs) has shown that shedding these restrictions results in powerful design tools, but at the expense of theoretical guarantees. In this work, we generalize classical mechanics to what we call geometric fabrics, whose expressivity and theory enable the design of systems that outperform RMPs in practice. Geometric fabrics strictly generalize classical mechanics forming a new physics of behavior by first generalizing them to Finsler geometries and then explicitly bending them to shape their behavior. We develop the theory of fabrics and present both a collection of controlled experiments examining their theoretical properties and a set of robot system experiments showing improved performance over a well-engineered and hardened implementation of RMPs, our current state-of-the-art in controller design.
CoDE: Collocation for Demonstration Encoding
May 07, 2021
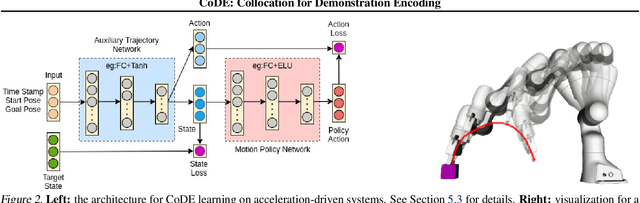
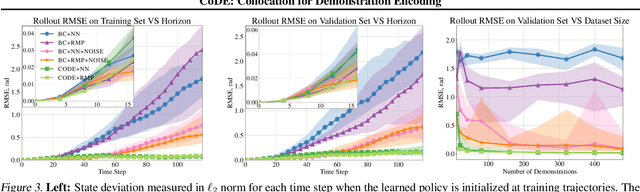
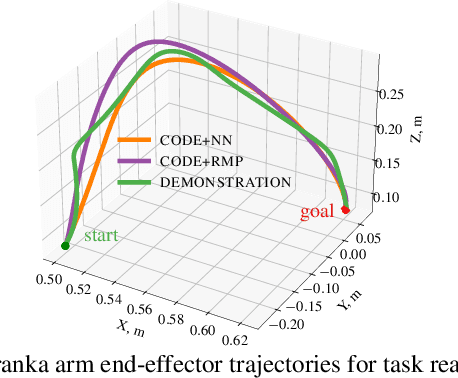
Abstract:Roboticists frequently turn to Imitation learning (IL) for data efficient policy learning. Many IL methods, canonicalized by the seminal work on Dataset Aggregation (DAgger), combat distributional shift issues with older Behavior Cloning (BC) methods by introducing oracle experts. Unfortunately, access to oracle experts is often unrealistic in practice; data frequently comes from manual offline methods such as lead-through or teleoperation. We present a data-efficient imitation learning technique called Collocation for Demonstration Encoding (CoDE) that operates on only a fixed set of trajectory demonstrations by modeling learning as empirical risk minimization. We circumvent problematic back-propagation through time problems by introducing an auxiliary trajectory network taking inspiration from collocation techniques in optimal control. Our method generalizes well and is much more data efficient than standard BC methods. We present experiments on a 7-degree-of-freedom (DoF) robotic manipulator learning behavior shaping policies for efficient tabletop operation.
Geometric Fabrics for the Acceleration-based Design of Robotic Motion
Nov 11, 2020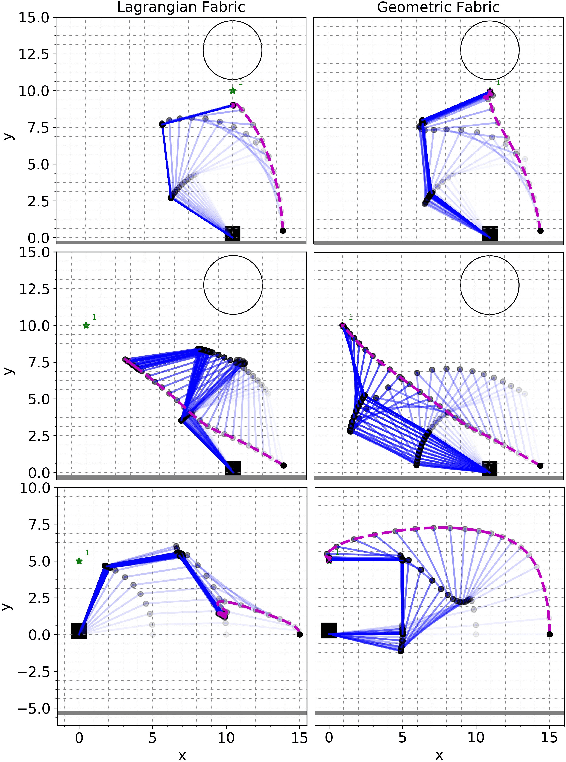

Abstract:This paper describes the pragmatic design and construction of geometric fabrics for shaping a robot's task-independent nominal behavior, capturing behavioral components such as obstacle avoidance, joint limit avoidance, redundancy resolution, global navigation heuristics, etc. Geometric fabrics constitute the most concrete incarnation of a new mathematical formulation for reactive behavior called optimization fabrics. Fabrics generalize recent work on Riemannian Motion Policies (RMPs); they add provable stability guarantees and improve design consistency while promoting the intuitive acceleration-based principles of modular design that make RMPs successful. We describe a suite of mathematical modeling tools that practitioners can employ in practice and demonstrate both how to mitigate system complexity by constructing behaviors layer-wise and how to employ these tools to design robust, strongly-generalizing, policies that solve practical problems one would expect to find in industry applications. Our system exhibits intelligent global navigation behaviors expressed entirely as fabrics with zero planning or state machine governance.
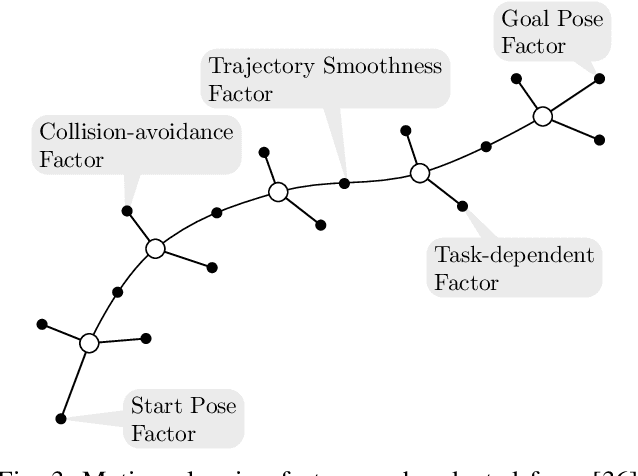
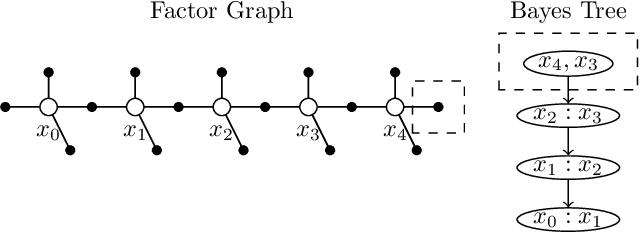
A Factor-Graph Approach for Optimization Problems with Dynamics Constraints
Nov 11, 2020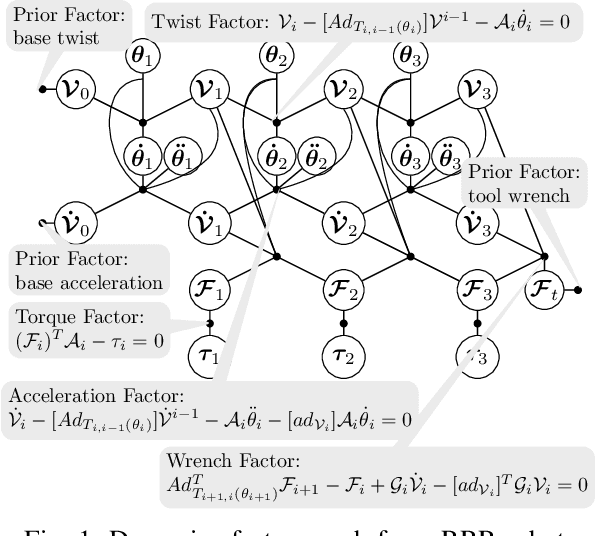
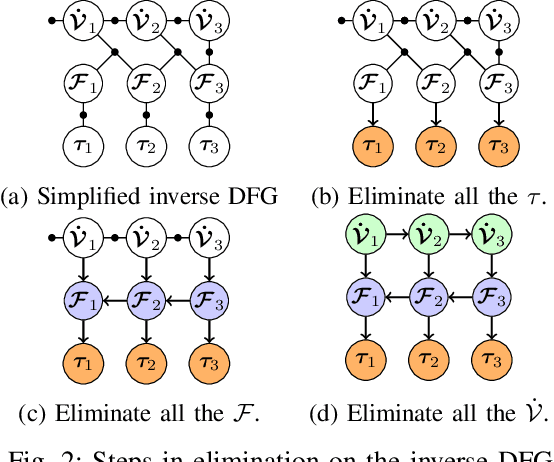
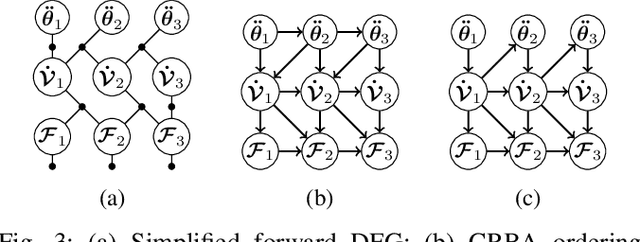
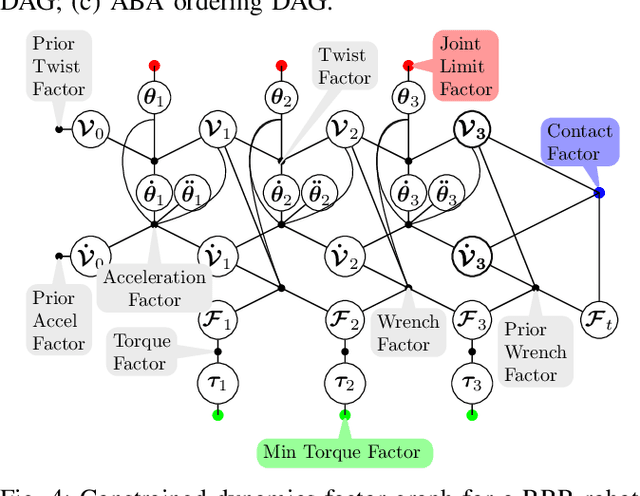
Abstract:In this paper, we introduce dynamics factor graphs as a graphical framework to solve dynamics problems and kinodynamic motion planning problems with full consideration of whole-body dynamics and contacts. A factor graph representation of dynamics problems provides an insightful visualization of their mathematical structure and can be used in conjunction with sparse nonlinear optimizers to solve challenging, high-dimensional optimization problems in robotics. We can easily formulate kinodynamic motion planning as a trajectory optimization problem with factor graphs. We demonstrate the flexibility and descriptive power of dynamics factor graphs by applying them to control various dynamical systems, ranging from a simple cart pole to a 12-DoF quadrupedal robot.
Generalized Nonlinear and Finsler Geometry for Robotics
Nov 04, 2020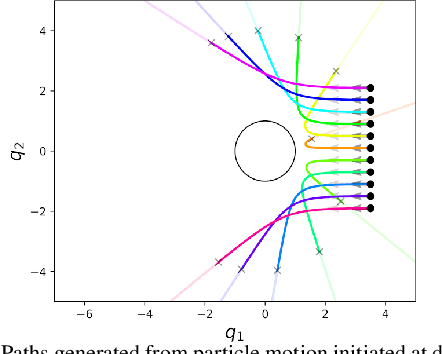

Abstract:Robotics research has found numerous important applications of Riemannian geometry. Despite that, the concept remain challenging to many roboticists because the background material is complex and strikingly foreign. Beyond Riemannian geometry, there are many natural generalizations in the mathematical literature---areas such as Finsler geometry and spray geometry---but those generalizations are largely inaccessible, and as a result there remain few applications within robotics. This paper presents a re-derivation of spray and Finsler geometries, critical for the development of our recent work on geometric fabrics, which builds the ideas from familiar concepts in advanced calculus and the calculus of variations. We focus on the pragmatic and calculable results, avoiding the use of tensor notation to appeal to a broader audience and emphasizing geometric path consistency over ideas around connections and curvature. It is our hope that they will contribute to an increased understanding generalized nonlinear, and even classical Riemannian, geometry within the robotics community and inspire future research into new applications.
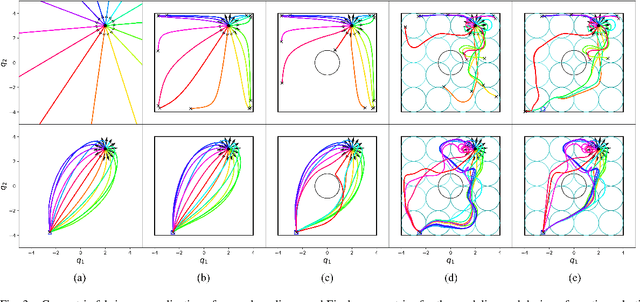
Optimization Fabrics for Behavioral Design
Nov 04, 2020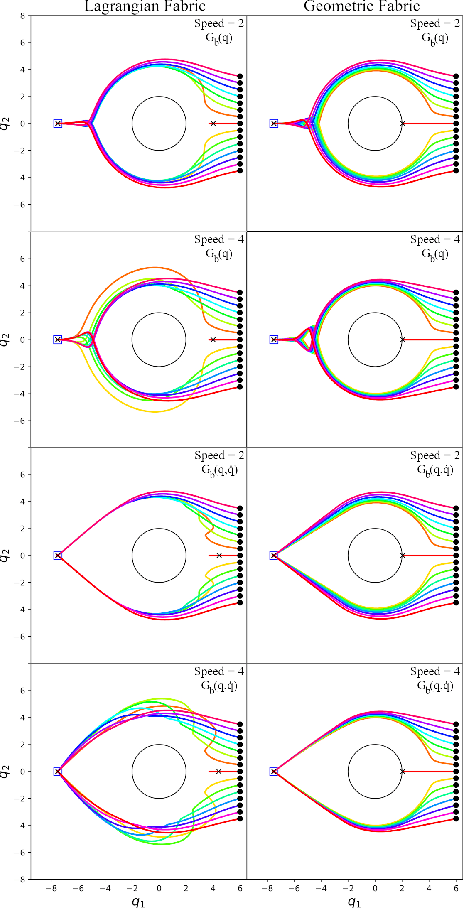
Abstract:Second-order differential equations define smooth system behavior. In general, there is no guarantee that a system will behave well when forced by a potential function, but in some cases they do and may exhibit smooth optimization properties such as convergence to a local minimum of the potential. Such a property is desirable and inherently linked to asymptotic stability. This paper presents a comprehensive theory of optimization fabrics which are second-order differential equations that encode nominal behaviors on a space and are guaranteed to optimize when forced by a potential function. Optimization fabrics, or fabrics for short, can encode commonalities among optimization problems that reflect the structure of the space itself, enabling smooth optimization processes to intelligently navigate each problem even when the potential function is simple and relatively naive. Importantly, optimization over a fabric is asymptotically stable, so optimization fabrics constitute a building block for stable system design.
Optimization Fabrics
Aug 22, 2020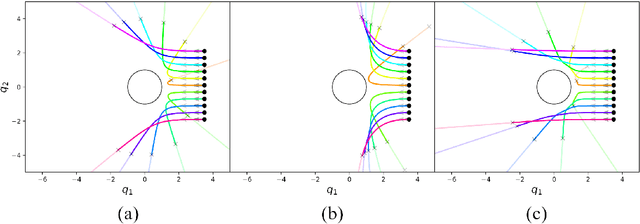
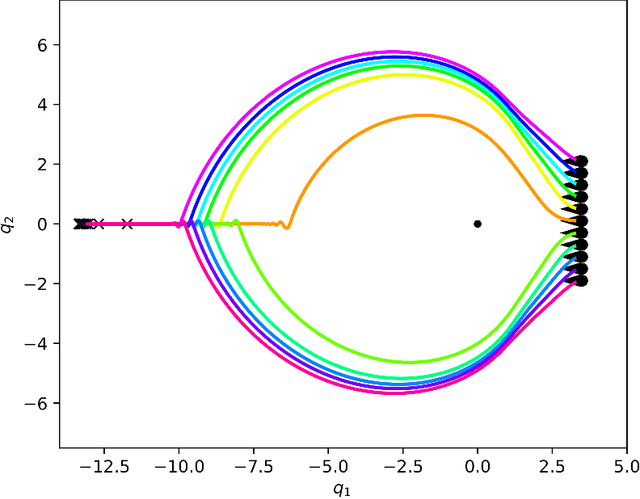
Abstract:This paper presents a theory of optimization fabrics, second-order differential equations that encode nominal behaviors on a space and can be used to define the behavior of a smooth optimizer. Optimization fabrics can encode commonalities among optimization problems that reflect the structure of the space itself, enabling smooth optimization processes to intelligently navigate each problem even when optimizing simple naive potential functions. Importantly, optimization over a fabric is inherently asymptotically stable. The majority of this paper is dedicated to the development of a tool set for the design and use of a broad class of fabrics called geometric fabrics. Geometric fabrics encode behavior as general nonlinear geometries which are covariant second-order differential equations with a special homogeneity property that ensures their behavior is independent of the system's speed through the medium. A class of Finsler Lagrangian energies can be used to both define how these nonlinear geometries combine with one another and how they react when potential functions force them from their nominal paths. Furthermore, these geometric fabrics are closed under the standard operations of pullback and combination on a transform tree. For behavior representation, this class of geometric fabrics constitutes a broad class of spectral semi-sprays (specs), also known as Riemannian Motion Policies (RMPs) in the context of robotic motion generation, that captures both the intuitive separation between acceleration policy and priority metric critical for modular design and are inherently stable. Therefore, geometric fabrics are safe and easier to use by less experienced behavioral designers. Application of this theory to policy representation and generalization in learning are discussed as well.
Batch and Incremental Kinodynamic Motion Planning using Dynamic Factor Graphs
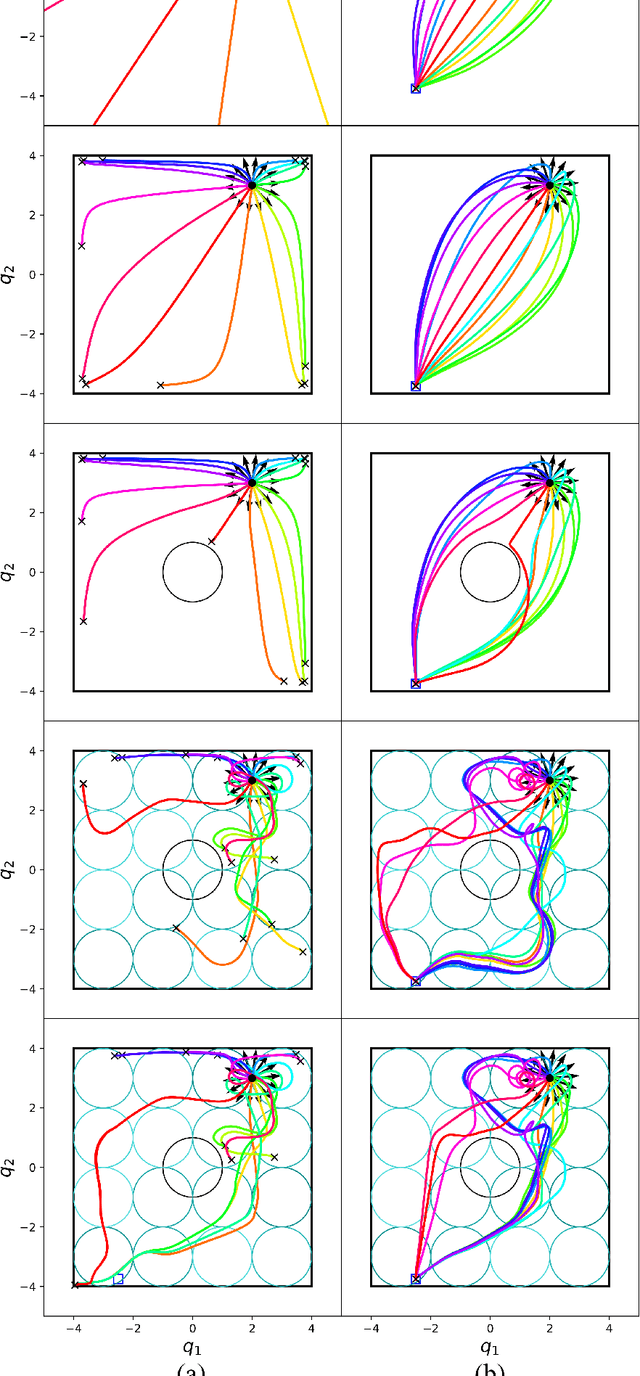
Jun 15, 2020
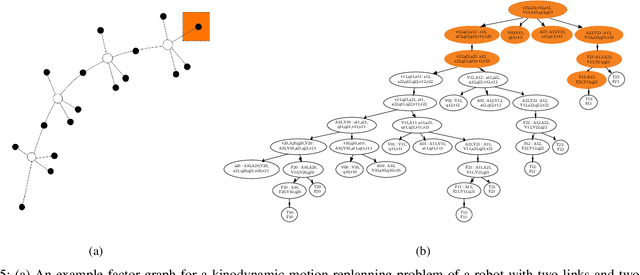
Abstract:This paper presents a kinodynamic motion planner that is able to produce energy efficient motions by taking the full robot dynamics into account, and making use of gravity, inertia, and momentum to reduce the effort. Given a specific goal state for the robot, we use factor graphs and numerical optimization to solve for an optimal trajectory, which meets not only the requirements of collision avoidance, but also all kinematic and dynamic constraints, such as velocity, acceleration and torque limits. By exploiting the sparsity in factor graphs, we can solve a kinodynamic motion planning problem efficiently, on par with existing optimal control methods, and use incremental elimination techniques to achieve an order of magnitude faster replanning.
A Unified Method for Solving Inverse, Forward, and Hybrid Manipulator Dynamics using Factor Graphs
Nov 22, 2019



Abstract:This paper describes a unified method solving for inverse, forward, and hybrid dynamics problems for robotic manipulators with either open kinematic chains or closed kinematic loops based on factor graphs. Manipulator dynamics is considered to be a well studied problem, and various different algorithms have been developed to solve each type of dynamics problem. However, they are not easily explained in an unified and intuitive way. In this paper, we introduce factor graphs as a unifying graphical language in which not only to solve all types of dynamics problems, but also explain the classical dynamics algorithms in a unified framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge