DextrAH-G: Pixels-to-Action Dexterous Arm-Hand Grasping with Geometric Fabrics

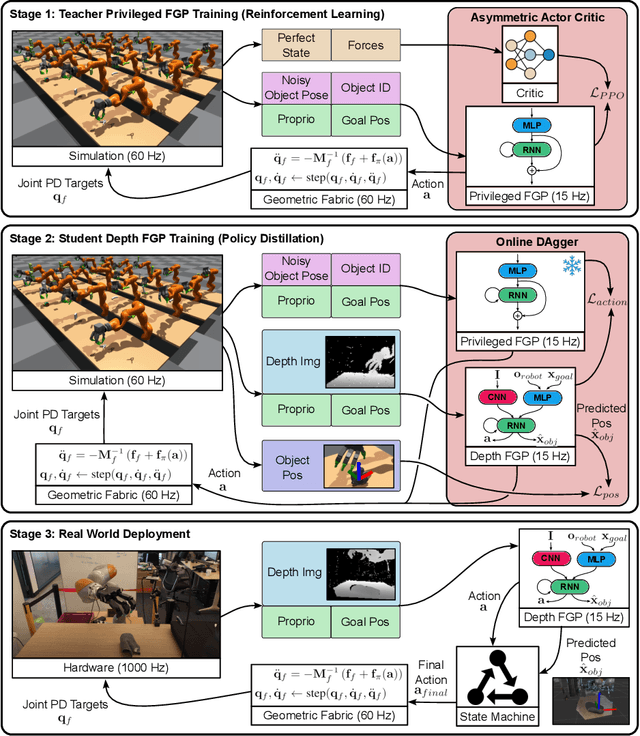
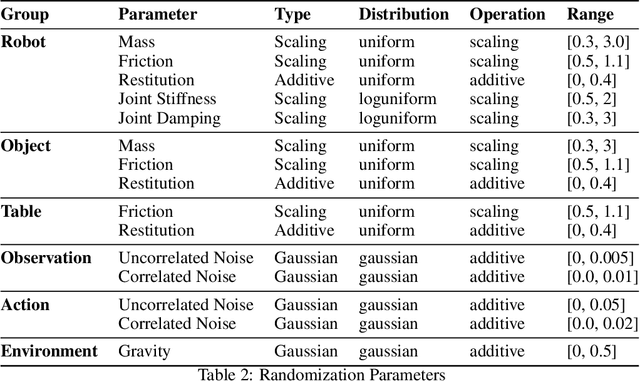
A pivotal challenge in robotics is achieving fast, safe, and robust dexterous grasping across a diverse range of objects, an important goal within industrial applications. However, existing methods often have very limited speed, dexterity, and generality, along with limited or no hardware safety guarantees. In this work, we introduce DextrAH-G, a depth-based dexterous grasping policy trained entirely in simulation that combines reinforcement learning, geometric fabrics, and teacher-student distillation. We address key challenges in joint arm-hand policy learning, such as high-dimensional observation and action spaces, the sim2real gap, collision avoidance, and hardware constraints. DextrAH-G enables a 23 motor arm-hand robot to safely and continuously grasp and transport a large variety of objects at high speed using multi-modal inputs including depth images, allowing generalization across object geometry. Videos at https://sites.google.com/view/dextrah-g.

Geometric Fabrics: a Safe Guiding Medium for Policy Learning

Robotics policies are always subjected to complex, second order dynamics that entangle their actions with resulting states. In reinforcement learning (RL) contexts, policies have the burden of deciphering these complicated interactions over massive amounts of experience and complex reward functions to learn how to accomplish tasks. Moreover, policies typically issue actions directly to controllers like Operational Space Control (OSC) or joint PD control, which induces straightline motion towards these action targets in task or joint space. However, straightline motion in these spaces for the most part do not capture the rich, nonlinear behavior our robots need to exhibit, shifting the burden of discovering these behaviors more completely to the agent. Unlike these simpler controllers, geometric fabrics capture a much richer and desirable set of behaviors via artificial, second order dynamics grounded in nonlinear geometry. These artificial dynamics shift the uncontrolled dynamics of a robot via an appropriate control law to form behavioral dynamics. Behavioral dynamics unlock a new action space and safe, guiding behavior over which RL policies are trained. Behavioral dynamics enable bang-bang-like RL policy actions that are still safe for real robots, simplify reward engineering, and help sequence real-world, high-performance policies. We describe the framework more generally and create a specific instantiation for the problem of dexterous, in-hand reorientation of a cube by a highly actuated robot hand.

Geometric Fabrics: Generalizing Classical Mechanics to Capture the Physics of Behavior

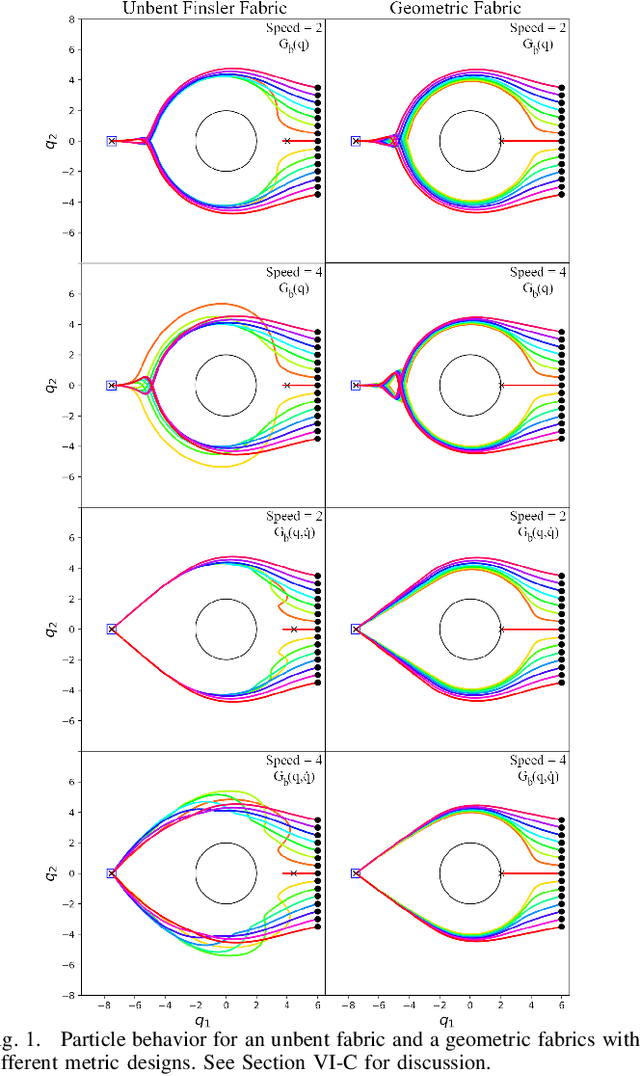
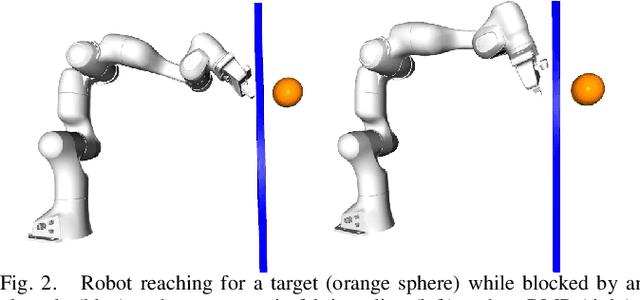
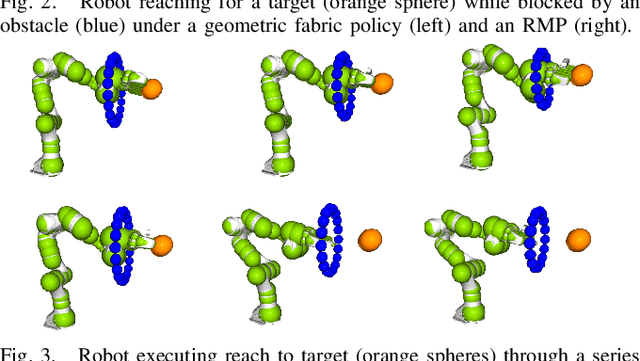
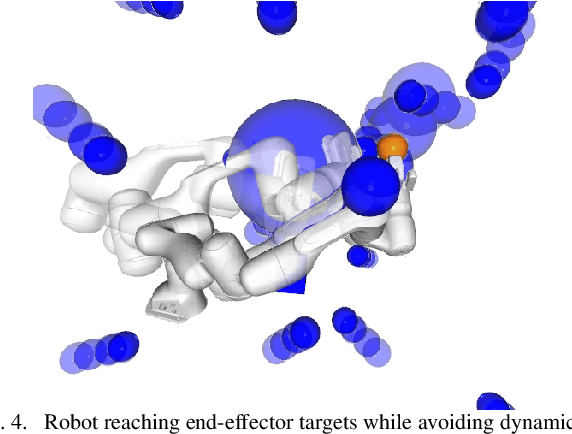
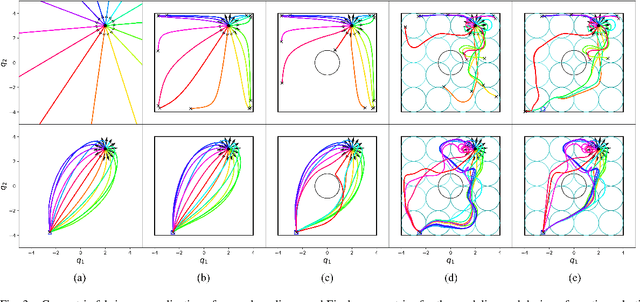
Classical mechanical systems are central to controller design in energy shaping methods of geometric control. However, their expressivity is limited by position-only metrics and the intimate link between metric and geometry. Recent work on Riemannian Motion Policies (RMPs) has shown that shedding these restrictions results in powerful design tools, but at the expense of theoretical guarantees. In this work, we generalize classical mechanics to what we call geometric fabrics, whose expressivity and theory enable the design of systems that outperform RMPs in practice. Geometric fabrics strictly generalize classical mechanics forming a new physics of behavior by first generalizing them to Finsler geometries and then explicitly bending them to shape their behavior. We develop the theory of fabrics and present both a collection of controlled experiments examining their theoretical properties and a set of robot system experiments showing improved performance over a well-engineered and hardened implementation of RMPs, our current state-of-the-art in controller design.

Generalized Nonlinear and Finsler Geometry for Robotics

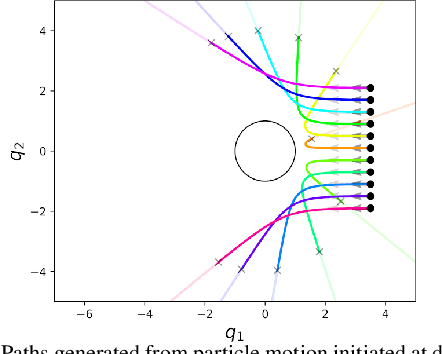
Robotics research has found numerous important applications of Riemannian geometry. Despite that, the concept remain challenging to many roboticists because the background material is complex and strikingly foreign. Beyond Riemannian geometry, there are many natural generalizations in the mathematical literature---areas such as Finsler geometry and spray geometry---but those generalizations are largely inaccessible, and as a result there remain few applications within robotics. This paper presents a re-derivation of spray and Finsler geometries, critical for the development of our recent work on geometric fabrics, which builds the ideas from familiar concepts in advanced calculus and the calculus of variations. We focus on the pragmatic and calculable results, avoiding the use of tensor notation to appeal to a broader audience and emphasizing geometric path consistency over ideas around connections and curvature. It is our hope that they will contribute to an increased understanding generalized nonlinear, and even classical Riemannian, geometry within the robotics community and inspire future research into new applications.

Optimization Fabrics for Behavioral Design

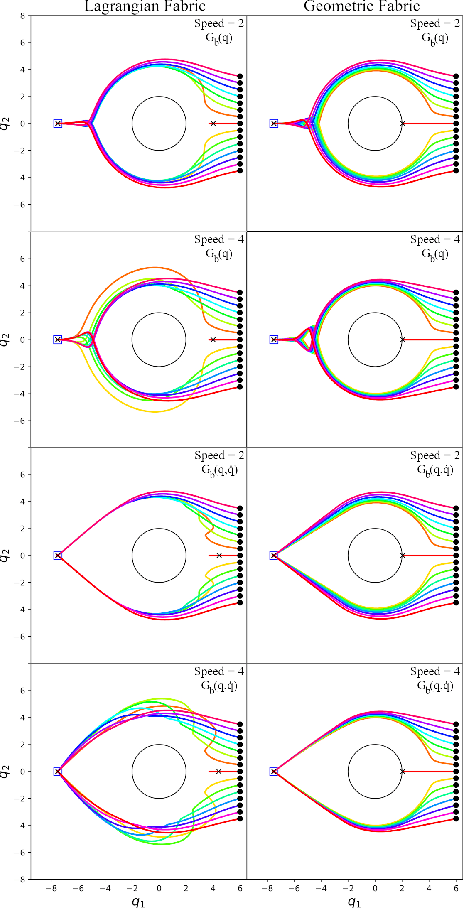
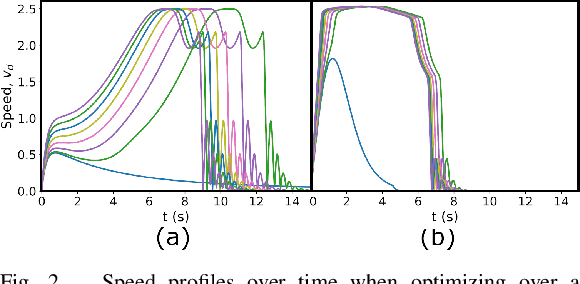
Second-order differential equations define smooth system behavior. In general, there is no guarantee that a system will behave well when forced by a potential function, but in some cases they do and may exhibit smooth optimization properties such as convergence to a local minimum of the potential. Such a property is desirable and inherently linked to asymptotic stability. This paper presents a comprehensive theory of optimization fabrics which are second-order differential equations that encode nominal behaviors on a space and are guaranteed to optimize when forced by a potential function. Optimization fabrics, or fabrics for short, can encode commonalities among optimization problems that reflect the structure of the space itself, enabling smooth optimization processes to intelligently navigate each problem even when the potential function is simple and relatively naive. Importantly, optimization over a fabric is asymptotically stable, so optimization fabrics constitute a building block for stable system design.

Optimization Fabrics

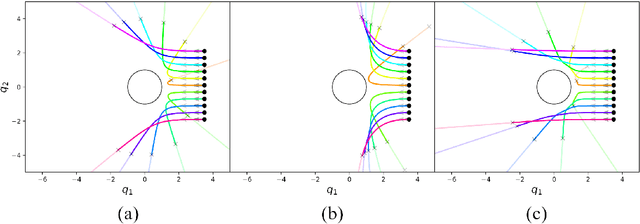
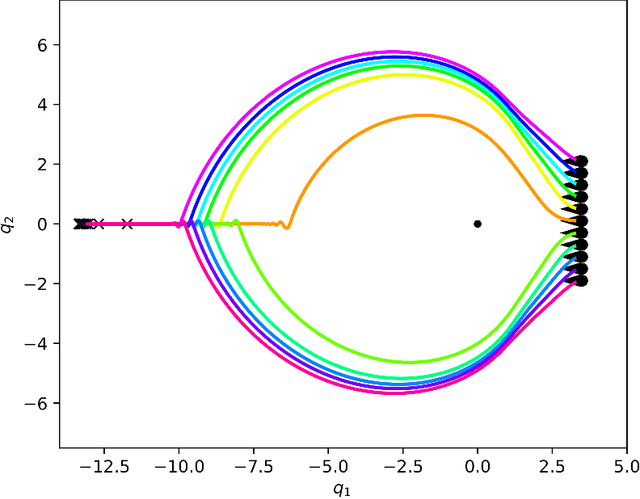
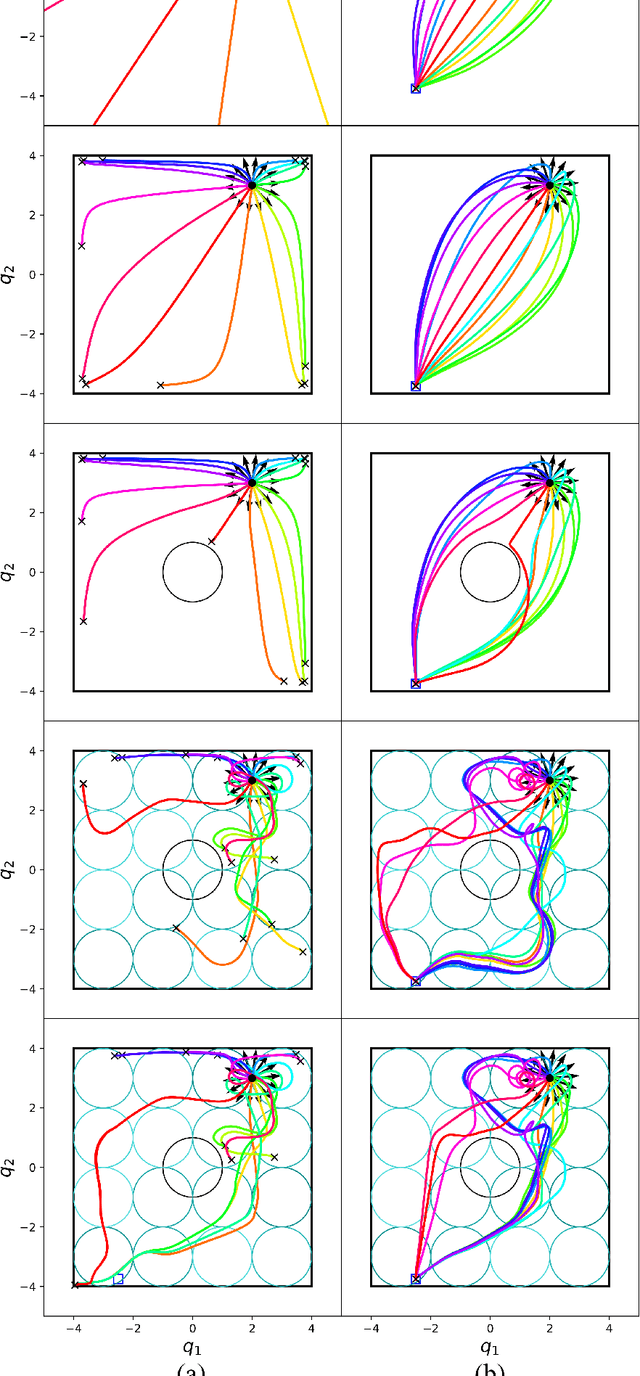
This paper presents a theory of optimization fabrics, second-order differential equations that encode nominal behaviors on a space and can be used to define the behavior of a smooth optimizer. Optimization fabrics can encode commonalities among optimization problems that reflect the structure of the space itself, enabling smooth optimization processes to intelligently navigate each problem even when optimizing simple naive potential functions. Importantly, optimization over a fabric is inherently asymptotically stable. The majority of this paper is dedicated to the development of a tool set for the design and use of a broad class of fabrics called geometric fabrics. Geometric fabrics encode behavior as general nonlinear geometries which are covariant second-order differential equations with a special homogeneity property that ensures their behavior is independent of the system's speed through the medium. A class of Finsler Lagrangian energies can be used to both define how these nonlinear geometries combine with one another and how they react when potential functions force them from their nominal paths. Furthermore, these geometric fabrics are closed under the standard operations of pullback and combination on a transform tree. For behavior representation, this class of geometric fabrics constitutes a broad class of spectral semi-sprays (specs), also known as Riemannian Motion Policies (RMPs) in the context of robotic motion generation, that captures both the intuitive separation between acceleration policy and priority metric critical for modular design and are inherently stable. Therefore, geometric fabrics are safe and easier to use by less experienced behavioral designers. Application of this theory to policy representation and generalization in learning are discussed as well.

Riemannian Motion Policies

We introduce the Riemannian Motion Policy (RMP), a new mathematical object for modular motion generation. An RMP is a second-order dynamical system (acceleration field or motion policy) coupled with a corresponding Riemannian metric. The motion policy maps positions and velocities to accelerations, while the metric captures the directions in the space important to the policy. We show that RMPs provide a straightforward and convenient method for combining multiple motion policies and transforming such policies from one space (such as the task space) to another (such as the configuration space) in geometrically consistent ways. The operators we derive for these combinations and transformations are provably optimal, have linearity properties making them agnostic to the order of application, and are strongly analogous to the covariant transformations of natural gradients popular in the machine learning literature. The RMP framework enables the fusion of motion policies from different motion generation paradigms, such as dynamical systems, dynamic movement primitives (DMPs), optimal control, operational space control, nonlinear reactive controllers, motion optimization, and model predictive control (MPC), thus unifying these disparate techniques from the literature. RMPs are easy to implement and manipulate, facilitate controller design, simplify handling of joint limits, and clarify a number of open questions regarding the proper fusion of motion generation methods (such as incorporating local reactive policies into long-horizon optimizers). We demonstrate the effectiveness of RMPs on both simulation and real robots, including their ability to naturally and efficiently solve complicated collision avoidance problems previously handled by more complex planners.