A Reduction-Driven Local Search for the Generalized Independent Set Problem

The Generalized Independent Set (GIS) problem extends the classical maximum independent set problem by incorporating profits for vertices and penalties for edges. This generalized problem has been identified in diverse applications in fields such as forest harvest planning, competitive facility location, social network analysis, and even machine learning. However, solving the GIS problem in large-scale, real-world networks remains computationally challenging. In this paper, we explore data reduction techniques to address this challenge. We first propose 14 reduction rules that can reduce the input graph with rigorous optimality guarantees. We then present a reduction-driven local search (RLS) algorithm that integrates these reduction rules into the pre-processing, the initial solution generation, and the local search components in a computationally efficient way. The RLS is empirically evaluated on 278 graphs arising from different application scenarios. The results indicates that the RLS is highly competitive -- For most graphs, it achieves significantly superior solutions compared to other known solvers, and it effectively provides solutions for graphs exceeding 260 million edges, a task at which every other known method fails. Analysis also reveals that the data reduction plays a key role in achieving such a competitive performance.

Systematic Parameter Decision in Approximate Model Counting

This paper proposes a novel approach to determining the internal parameters of the hashing-based approximate model counting algorithm $\mathsf{ApproxMC}$. In this problem, the chosen parameter values must ensure that $\mathsf{ApproxMC}$ is Probably Approximately Correct (PAC), while also making it as efficient as possible. The existing approach to this problem relies on heuristics; in this paper, we solve this problem by formulating it as an optimization problem that arises from generalizing $\mathsf{ApproxMC}$'s correctness proof to arbitrary parameter values. Our approach separates the concerns of algorithm soundness and optimality, allowing us to address the former without the need for repetitive case-by-case argumentation, while establishing a clear framework for the latter. Furthermore, after reduction, the resulting optimization problem takes on an exceptionally simple form, enabling the use of a basic search algorithm and providing insight into how parameter values affect algorithm performance. Experimental results demonstrate that our optimized parameters improve the runtime performance of the latest $\mathsf{ApproxMC}$ by a factor of 1.6 to 2.4, depending on the error tolerance.

CSS: Overcoming Pose and Scene Challenges in Crowd-Sourced 3D Gaussian Splatting

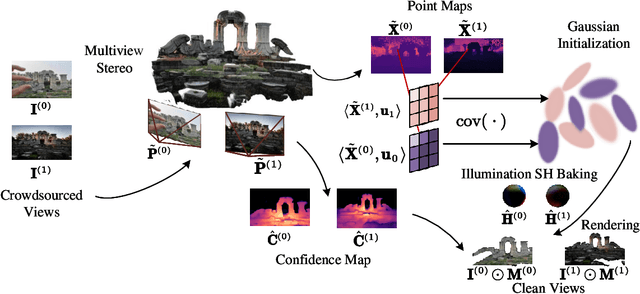
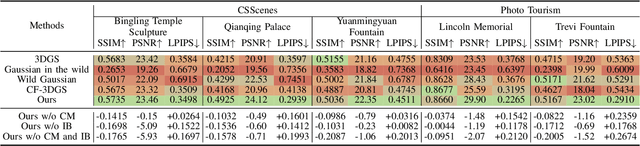
We introduce Crowd-Sourced Splatting (CSS), a novel 3D Gaussian Splatting (3DGS) pipeline designed to overcome the challenges of pose-free scene reconstruction using crowd-sourced imagery. The dream of reconstructing historically significant but inaccessible scenes from collections of photographs has long captivated researchers. However, traditional 3D techniques struggle with missing camera poses, limited viewpoints, and inconsistent lighting. CSS addresses these challenges through robust geometric priors and advanced illumination modeling, enabling high-quality novel view synthesis under complex, real-world conditions. Our method demonstrates clear improvements over existing approaches, paving the way for more accurate and flexible applications in AR, VR, and large-scale 3D reconstruction.

Map-Free Visual Relocalization Enhanced by Instance Knowledge and Depth Knowledge

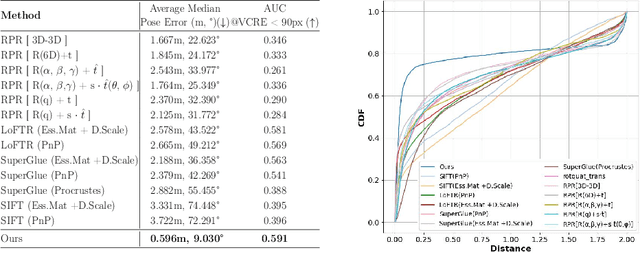
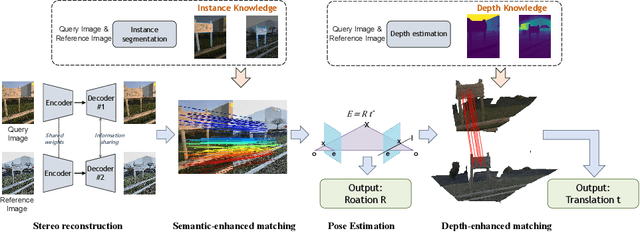
Map-free relocalization technology is crucial for applications in autonomous navigation and augmented reality, but relying on pre-built maps is often impractical. It faces significant challenges due to limitations in matching methods and the inherent lack of scale in monocular images. These issues lead to substantial rotational and metric errors and even localization failures in real-world scenarios. Large matching errors significantly impact the overall relocalization process, affecting both rotational and translational accuracy. Due to the inherent limitations of the camera itself, recovering the metric scale from a single image is crucial, as this significantly impacts the translation error. To address these challenges, we propose a map-free relocalization method enhanced by instance knowledge and depth knowledge. By leveraging instance-based matching information to improve global matching results, our method significantly reduces the possibility of mismatching across different objects. The robustness of instance knowledge across the scene helps the feature point matching model focus on relevant regions and enhance matching accuracy. Additionally, we use estimated metric depth from a single image to reduce metric errors and improve scale recovery accuracy. By integrating methods dedicated to mitigating large translational and rotational errors, our approach demonstrates superior performance in map-free relocalization techniques.

A Faster Branching Algorithm for the Maximum $k$-Defective Clique Problem

A $k$-defective clique of an undirected graph $G$ is a subset of its vertices that induces a nearly complete graph with a maximum of $k$ missing edges. The maximum $k$-defective clique problem, which asks for the largest $k$-defective clique from the given graph, is important in many applications, such as social and biological network analysis. In the paper, we propose a new branching algorithm that takes advantage of the structural properties of the $k$-defective clique and uses the efficient maximum clique algorithm as a subroutine. As a result, the algorithm has a better asymptotic running time than the existing ones. We also investigate upper-bounding techniques and propose a new upper bound utilizing the \textit{conflict relationship} between vertex pairs. Because conflict relationship is common in many graph problems, we believe that this technique can be potentially generalized. Finally, experiments show that our algorithm outperforms state-of-the-art solvers on a wide range of open benchmarks.

A Fast Maximum $k$-Plex Algorithm Parameterized by the Degeneracy Gap

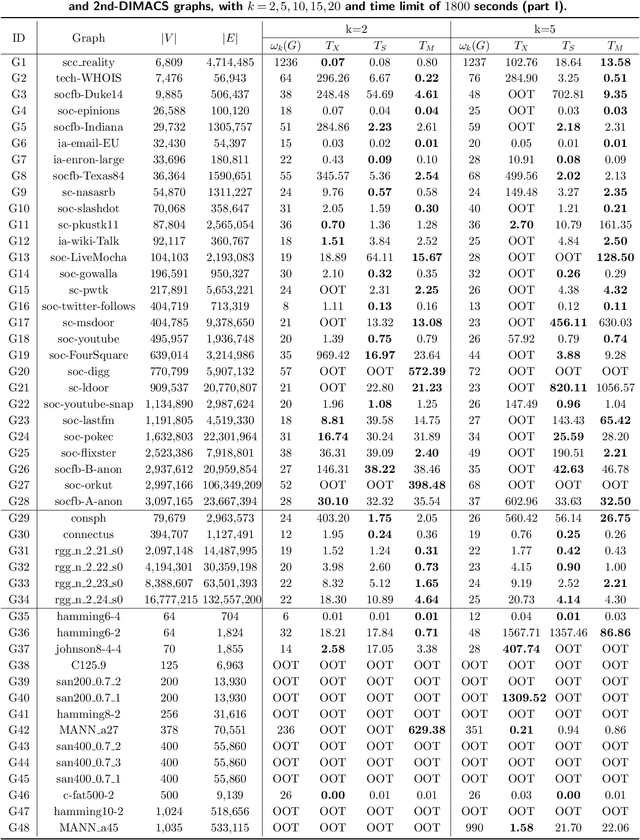
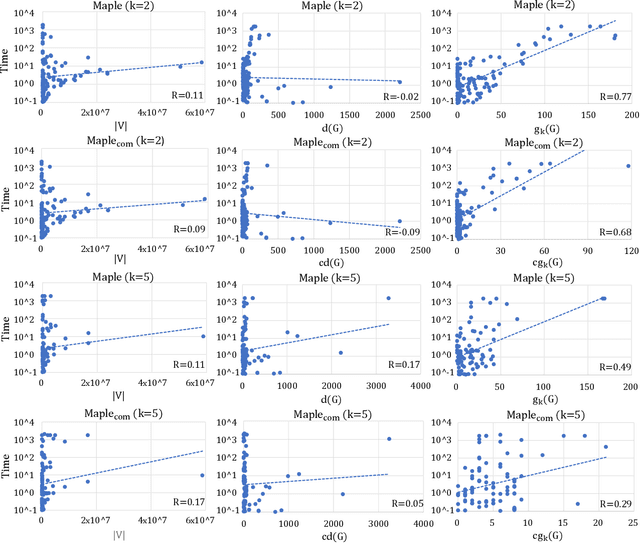
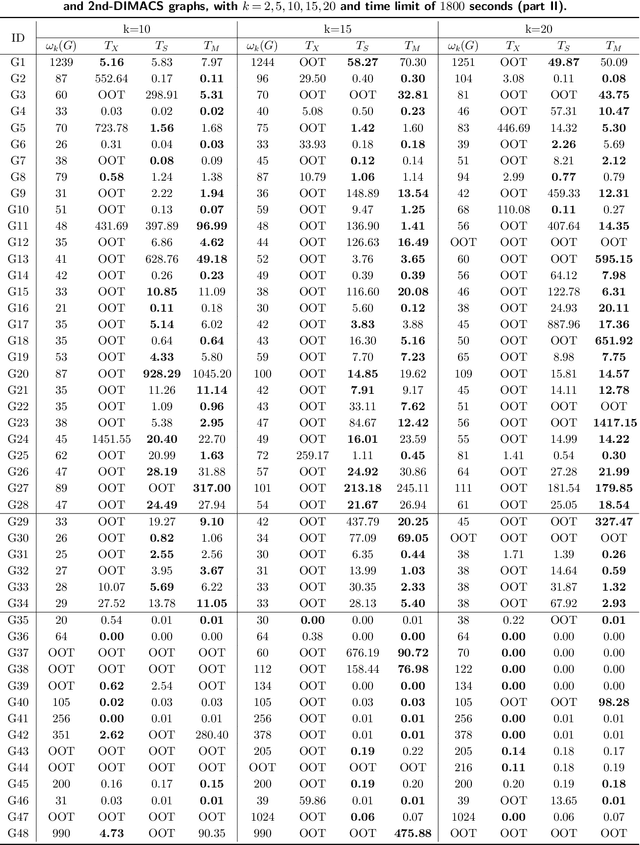
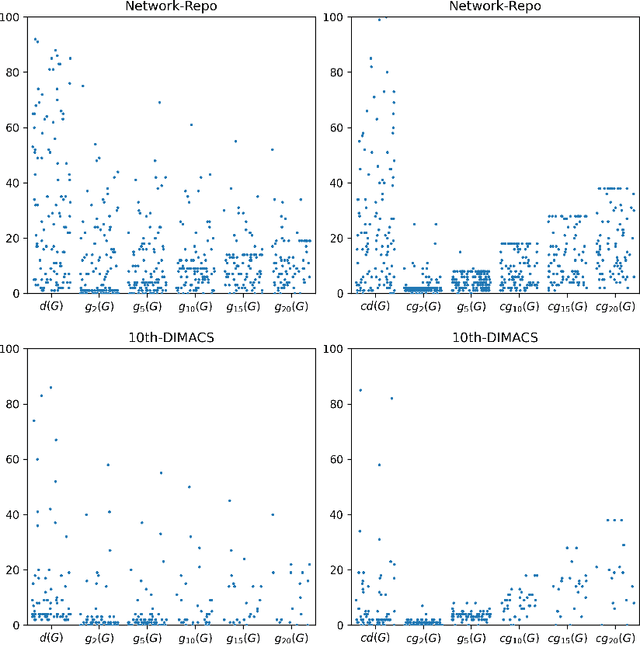
Given a graph, the $k$-plex is a vertex set in which each vertex is not adjacent to at most $k-1$ other vertices in the set. The maximum $k$-plex problem, which asks for the largest $k$-plex from a given graph, is an important but computationally challenging problem in applications like graph search and community detection. So far, there is a number of empirical algorithms without sufficient theoretical explanations on the efficiency. We try to bridge this gap by defining a novel parameter of the input instance, $g_k(G)$, the gap between the degeneracy bound and the size of maximum $k$-plex in the given graph, and presenting an exact algorithm parameterized by $g_k(G)$. In other words, we design an algorithm with running time polynomial in the size of input graph and exponential in $g_k(G)$ where $k$ is a constant. Usually, $g_k(G)$ is small and bounded by $O(\log{(|V|)})$ in real-world graphs, indicating that the algorithm runs in polynomial time. We also carry out massive experiments and show that the algorithm is competitive with the state-of-the-art solvers. Additionally, for large $k$ values such as $15$ and $20$, our algorithm has superior performance over existing algorithms.

Facility Location with Entrance Fees

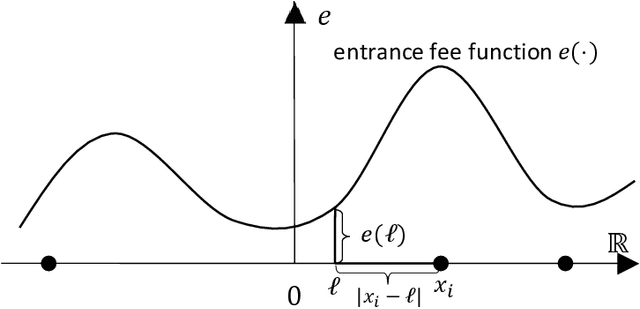
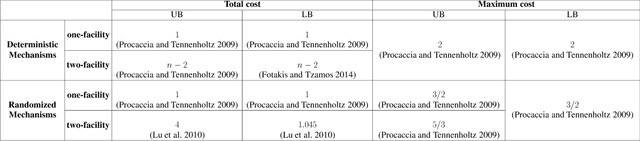
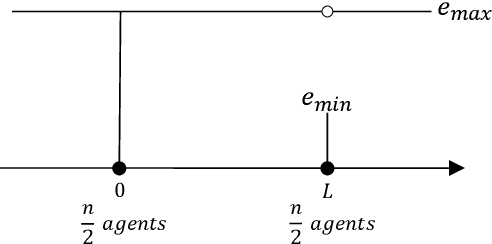
In mechanism design, the facility location game is an extensively studied problem. In the classical model, the cost of each agent is her distance to the nearest facility. In this paper, we consider a new model, where there is a location-dependent entrance fee to the facility. Thus, in our model, the cost of each agent is the sum of the distance to the facility and the entrance fee of the facility. This is a refined generalization of the classical model. We study the model and design strategyproof mechanisms. For one and two facilities, we provide upper and lower bounds for the approximation ratio given by deterministic and randomized mechanisms, with respect to the utilitarian objective and the egalitarian objective. Most of our bounds are tight and these bounds are independent of the entrance fee functions. Our results are as general as possible because the entrance fee function we consider is arbitrary.

Listing Maximal k-Plexes in Large Real-World Graphs

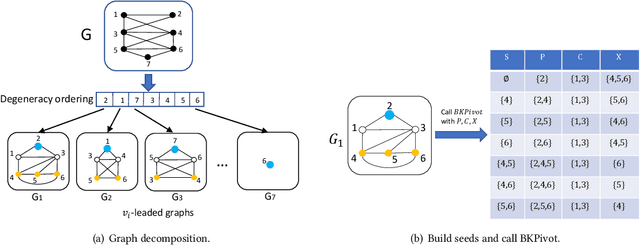
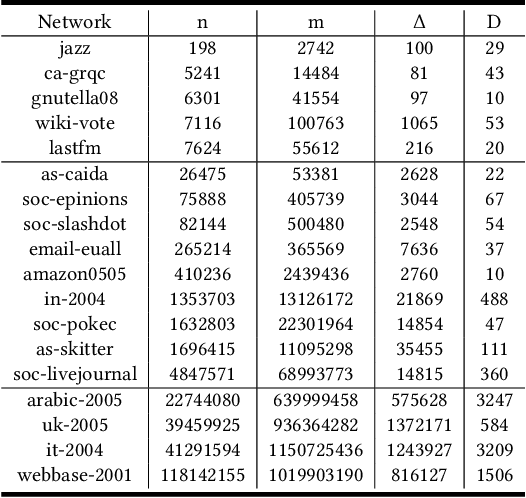
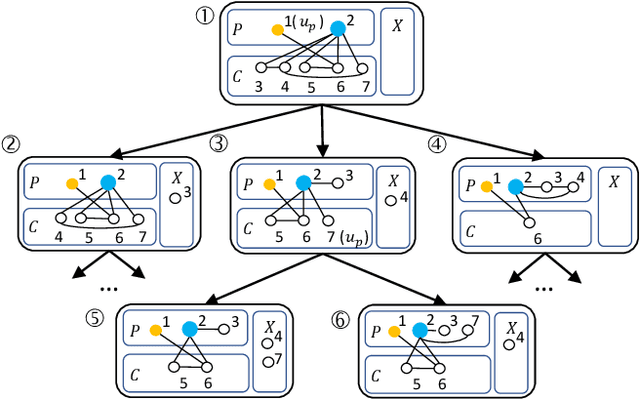
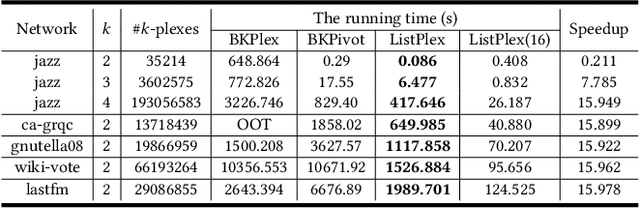
Listing dense subgraphs in large graphs plays a key task in varieties of network analysis applications like community detection. Clique, as the densest model, has been widely investigated. However, in practice, communities rarely form as cliques for various reasons, e.g., data noise. Therefore, $k$-plex, -- graph with each vertex adjacent to all but at most $k$ vertices, is introduced as a relaxed version of clique. Often, to better simulate cohesive communities, an emphasis is placed on connected $k$-plexes with small $k$. In this paper, we continue the research line of listing all maximal $k$-plexes and maximal $k$-plexes of prescribed size. Our first contribution is algorithm ListPlex that lists all maximal $k$-plexes in $O^*(\gamma^D)$ time for each constant $k$, where $\gamma$ is a value related to $k$ but strictly smaller than 2, and $D$ is the degeneracy of the graph that is far less than the vertex number $n$ in real-word graphs. Compared to the trivial bound of $2^n$, the improvement is significant, and our bound is better than all previously known results. In practice, we further use several techniques to accelerate listing $k$-plexes of a given size, such as structural-based prune rules, cache-efficient data structures, and parallel techniques. All these together result in a very practical algorithm. Empirical results show that our approach outperforms the state-of-the-art solutions by up to orders of magnitude.

Enhancing Balanced Graph Edge Partition with Effective Local Search

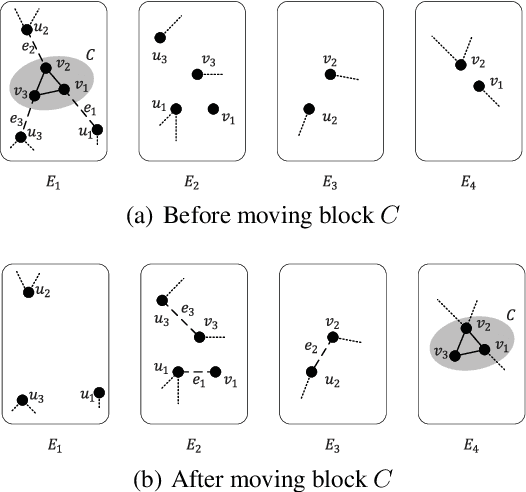
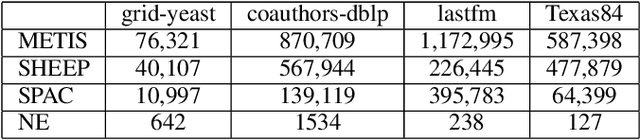
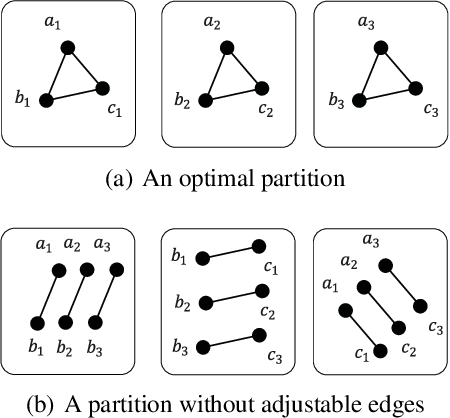
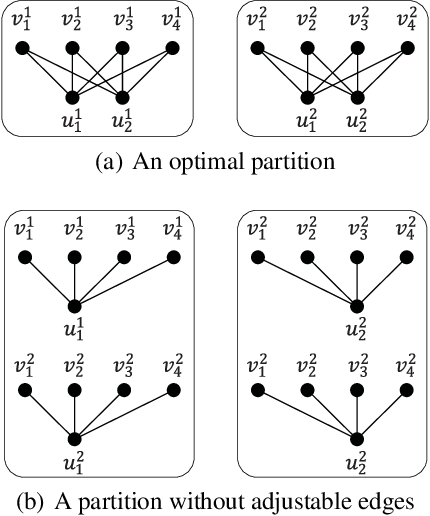
Graph partition is a key component to achieve workload balance and reduce job completion time in parallel graph processing systems. Among the various partition strategies, edge partition has demonstrated more promising performance in power-law graphs than vertex partition and thereby has been more widely adopted as the default partition strategy by existing graph systems. The graph edge partition problem, which is to split the edge set into multiple balanced parts to minimize the total number of copied vertices, has been widely studied from the view of optimization and algorithms. In this paper, we study local search algorithms for this problem to further improve the partition results from existing methods. More specifically, we propose two novel concepts, namely adjustable edges and blocks. Based on these, we develop a greedy heuristic as well as an improved search algorithm utilizing the property of the max-flow model. To evaluate the performance of our algorithms, we first provide adequate theoretical analysis in terms of the approximation quality. We significantly improve the previously known approximation ratio for this problem. Then we conduct extensive experiments on a large number of benchmark datasets and state-of-the-art edge partition strategies. The results show that our proposed local search framework can further improve the quality of graph partition by a wide margin.

Object Reachability via Swaps under Strict and Weak Preferences

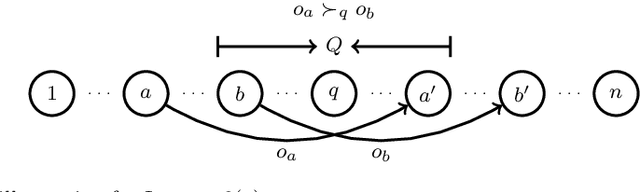
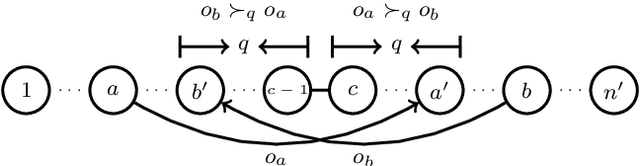
The \textsc{Housing Market} problem is a widely studied resource allocation problem. In this problem, each agent can only receive a single object and has preferences over all objects. Starting from an initial endowment, we want to reach a certain assignment via a sequence of rational trades. We first consider whether an object is reachable for a given agent under a social network, where a trade between two agents is allowed if they are neighbors in the network and no participant has a deficit from the trade. Assume that the preferences of the agents are strict (no tie among objects is allowed). This problem is polynomially solvable in a star-network and NP-complete in a tree-network. It is left as a challenging open problem whether the problem is polynomially solvable when the network is a path. We answer this open problem positively by giving a polynomial-time algorithm. Then we show that when the preferences of the agents are weak (ties among objects are allowed), the problem becomes NP-hard even when the network is a path. In addition, we consider the computational complexity of finding different optimal assignments for the problem under the network being a path or a star.