Pyramid Sparse Transformer: Enhancing Multi-Scale Feature Fusion with Dynamic Token Selection

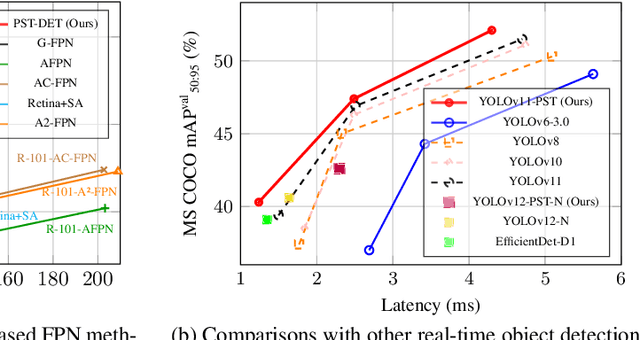
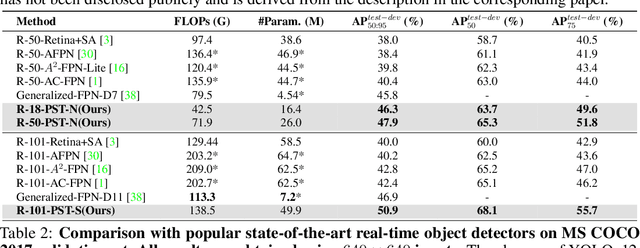
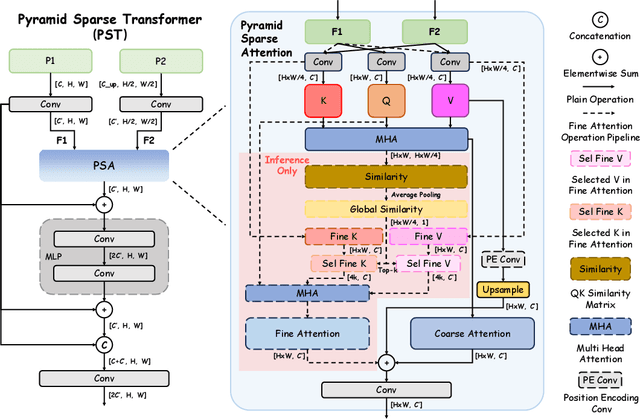
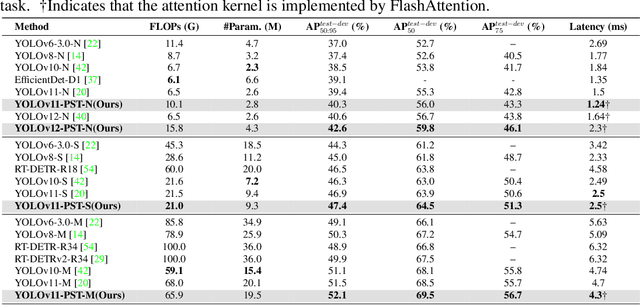
Feature fusion is critical for high-performance vision models but often incurs prohibitive complexity. However, prevailing attention-based fusion methods often involve significant computational complexity and implementation challenges, limiting their efficiency in resource-constrained environments. To address these issues, we introduce the Pyramid Sparse Transformer (PST), a lightweight, plug-and-play module that integrates coarse-to-fine token selection and shared attention parameters to reduce computation while preserving spatial detail. PST can be trained using only coarse attention and seamlessly activated at inference for further accuracy gains without retraining. When added to state-of-the-art real-time detection models, such as YOLOv11-N/S/M, PST yields mAP improvements of 0.9%, 0.5%, and 0.4% on MS COCO with minimal latency impact. Likewise, embedding PST into ResNet-18/50/101 as backbones, boosts ImageNet top-1 accuracy by 6.5%, 1.7%, and 1.0%, respectively. These results demonstrate PST's effectiveness as a simple, hardware-friendly enhancement for both detection and classification tasks.

Multivariate Conformal Selection

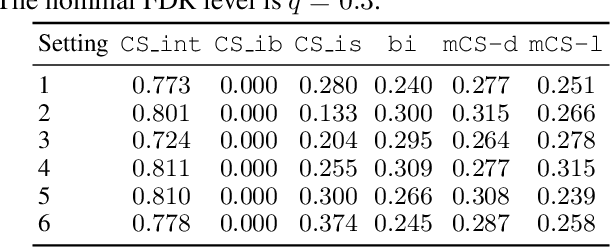
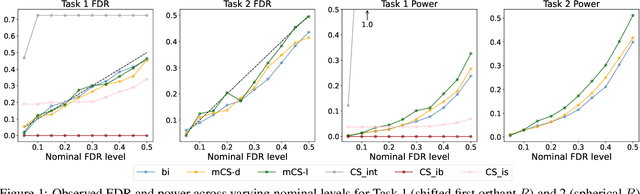
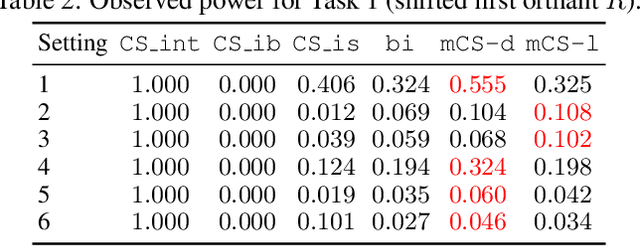
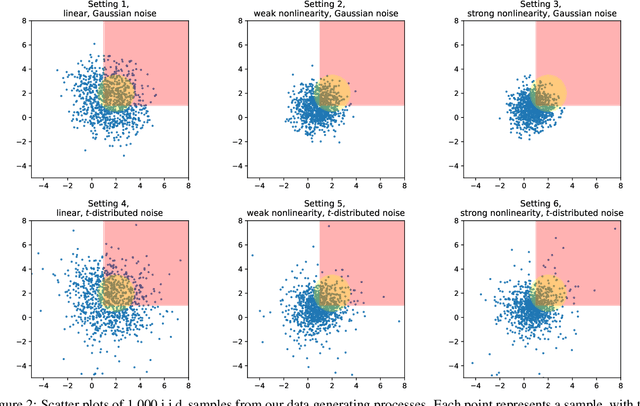
Selecting high-quality candidates from large datasets is critical in applications such as drug discovery, precision medicine, and alignment of large language models (LLMs). While Conformal Selection (CS) provides rigorous uncertainty quantification, it is limited to univariate responses and scalar criteria. To address this issue, we propose Multivariate Conformal Selection (mCS), a generalization of CS designed for multivariate response settings. Our method introduces regional monotonicity and employs multivariate nonconformity scores to construct conformal p-values, enabling finite-sample False Discovery Rate (FDR) control. We present two variants: mCS-dist, using distance-based scores, and mCS-learn, which learns optimal scores via differentiable optimization. Experiments on simulated and real-world datasets demonstrate that mCS significantly improves selection power while maintaining FDR control, establishing it as a robust framework for multivariate selection tasks.

Text-to-TrajVis: Enabling Trajectory Data Visualizations from Natural Language Questions

This paper introduces the Text-to-TrajVis task, which aims to transform natural language questions into trajectory data visualizations, facilitating the development of natural language interfaces for trajectory visualization systems. As this is a novel task, there is currently no relevant dataset available in the community. To address this gap, we first devised a new visualization language called Trajectory Visualization Language (TVL) to facilitate querying trajectory data and generating visualizations. Building on this foundation, we further proposed a dataset construction method that integrates Large Language Models (LLMs) with human efforts to create high-quality data. Specifically, we first generate TVLs using a comprehensive and systematic process, and then label each TVL with corresponding natural language questions using LLMs. This process results in the creation of the first large-scale Text-to-TrajVis dataset, named TrajVL, which contains 18,140 (question, TVL) pairs. Based on this dataset, we systematically evaluated the performance of multiple LLMs (GPT, Qwen, Llama, etc.) on this task. The experimental results demonstrate that this task is both feasible and highly challenging and merits further exploration within the research community.

Optimized Conformal Selection: Powerful Selective Inference After Conformity Score Optimization

Model selection/optimization in conformal inference is challenging, since it may break the exchangeability between labeled and unlabeled data. We study this problem in the context of conformal selection, which uses conformal p-values to select ``interesting'' instances with large unobserved labels from a pool of unlabeled data, while controlling the FDR in finite sample. For validity, existing solutions require the model choice to be independent of the data used to construct the p-values and calibrate the selection set. However, when presented with many model choices and limited labeled data, it is desirable to (i) select the best model in a data-driven manner, and (ii) mitigate power loss due to sample splitting. This paper presents OptCS, a general framework that allows valid statistical testing (selection) after flexible data-driven model optimization. We introduce general conditions under which OptCS constructs valid conformal p-values despite substantial data reuse and handles complex p-value dependencies to maintain finite-sample FDR control via a novel multiple testing procedure. We instantiate this general recipe to propose three FDR-controlling procedures, each optimizing the models differently: (i) selecting the most powerful one among multiple pre-trained candidate models, (ii) using all data for model fitting without sample splitting, and (iii) combining full-sample model fitting and selection. We demonstrate the efficacy of our methods via simulation studies and real applications in drug discovery and alignment of large language models in radiology report generation.

Facility Location with Entrance Fees

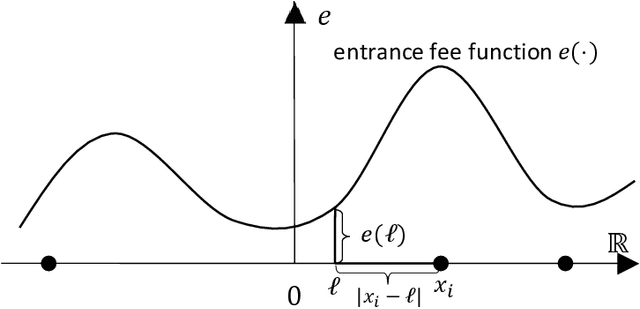
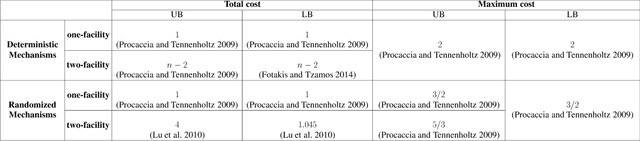
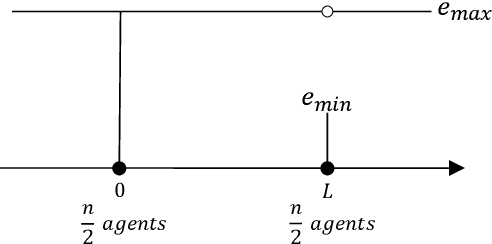
In mechanism design, the facility location game is an extensively studied problem. In the classical model, the cost of each agent is her distance to the nearest facility. In this paper, we consider a new model, where there is a location-dependent entrance fee to the facility. Thus, in our model, the cost of each agent is the sum of the distance to the facility and the entrance fee of the facility. This is a refined generalization of the classical model. We study the model and design strategyproof mechanisms. For one and two facilities, we provide upper and lower bounds for the approximation ratio given by deterministic and randomized mechanisms, with respect to the utilitarian objective and the egalitarian objective. Most of our bounds are tight and these bounds are independent of the entrance fee functions. Our results are as general as possible because the entrance fee function we consider is arbitrary.