Enhancing Balanced Graph Edge Partition with Effective Local Search
Paper and Code
Dec 17, 2020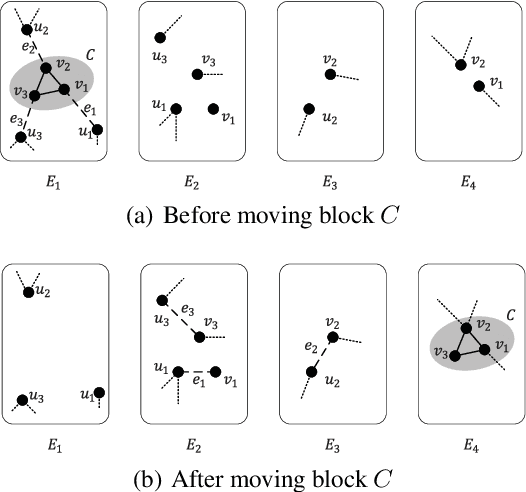
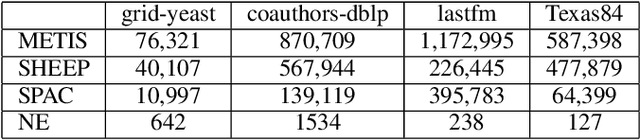
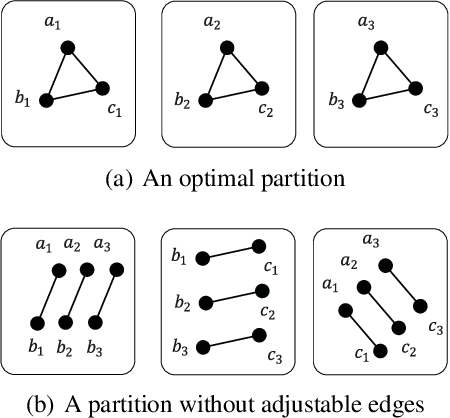
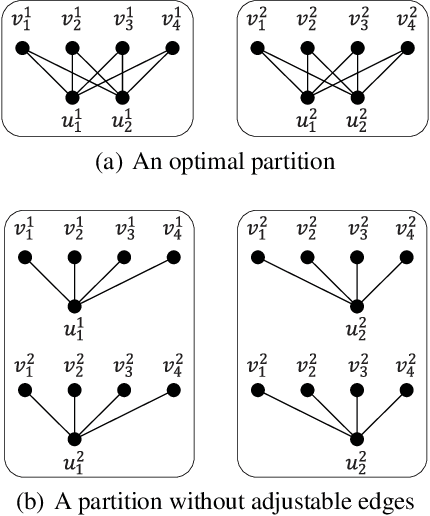
Graph partition is a key component to achieve workload balance and reduce job completion time in parallel graph processing systems. Among the various partition strategies, edge partition has demonstrated more promising performance in power-law graphs than vertex partition and thereby has been more widely adopted as the default partition strategy by existing graph systems. The graph edge partition problem, which is to split the edge set into multiple balanced parts to minimize the total number of copied vertices, has been widely studied from the view of optimization and algorithms. In this paper, we study local search algorithms for this problem to further improve the partition results from existing methods. More specifically, we propose two novel concepts, namely adjustable edges and blocks. Based on these, we develop a greedy heuristic as well as an improved search algorithm utilizing the property of the max-flow model. To evaluate the performance of our algorithms, we first provide adequate theoretical analysis in terms of the approximation quality. We significantly improve the previously known approximation ratio for this problem. Then we conduct extensive experiments on a large number of benchmark datasets and state-of-the-art edge partition strategies. The results show that our proposed local search framework can further improve the quality of graph partition by a wide margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge