Object Reachability via Swaps under Strict and Weak Preferences
Paper and Code
Sep 17, 2019
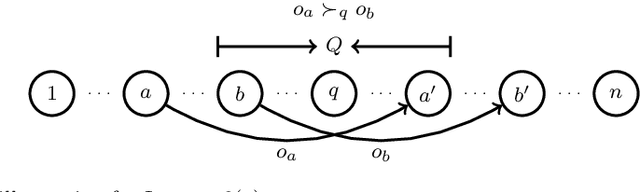

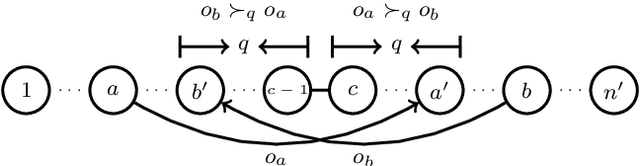
The \textsc{Housing Market} problem is a widely studied resource allocation problem. In this problem, each agent can only receive a single object and has preferences over all objects. Starting from an initial endowment, we want to reach a certain assignment via a sequence of rational trades. We first consider whether an object is reachable for a given agent under a social network, where a trade between two agents is allowed if they are neighbors in the network and no participant has a deficit from the trade. Assume that the preferences of the agents are strict (no tie among objects is allowed). This problem is polynomially solvable in a star-network and NP-complete in a tree-network. It is left as a challenging open problem whether the problem is polynomially solvable when the network is a path. We answer this open problem positively by giving a polynomial-time algorithm. Then we show that when the preferences of the agents are weak (ties among objects are allowed), the problem becomes NP-hard even when the network is a path. In addition, we consider the computational complexity of finding different optimal assignments for the problem under the network being a path or a star.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge