When Large Language Model Meets Optimization

Optimization algorithms and large language models (LLMs) enhance decision-making in dynamic environments by integrating artificial intelligence with traditional techniques. LLMs, with extensive domain knowledge, facilitate intelligent modeling and strategic decision-making in optimization, while optimization algorithms refine LLM architectures and output quality. This synergy offers novel approaches for advancing general AI, addressing both the computational challenges of complex problems and the application of LLMs in practical scenarios. This review outlines the progress and potential of combining LLMs with optimization algorithms, providing insights for future research directions.

A First-Order Algorithmic Framework for Wasserstein Distributionally Robust Logistic Regression

Wasserstein distance-based distributionally robust optimization (DRO) has received much attention lately due to its ability to provide a robustness interpretation of various learning models. Moreover, many of the DRO problems that arise in the learning context admits exact convex reformulations and hence can be tackled by off-the-shelf solvers. Nevertheless, the use of such solvers severely limits the applicability of DRO in large-scale learning problems, as they often rely on general purpose interior-point algorithms. On the other hand, there are very few works that attempt to develop fast iterative methods to solve these DRO problems, which typically possess complicated structures. In this paper, we take a first step towards resolving the above difficulty by developing a first-order algorithmic framework for tackling a class of Wasserstein distance-based distributionally robust logistic regression (DRLR) problem. Specifically, we propose a novel linearized proximal ADMM to solve the DRLR problem, whose objective is convex but consists of a smooth term plus two non-separable non-smooth terms. We prove that our method enjoys a sublinear convergence rate. Furthermore, we conduct three different experiments to show its superb performance on both synthetic and real-world datasets. In particular, our method can achieve the same accuracy up to 800+ times faster than the standard off-the-shelf solver.

Object Reachability via Swaps under Strict and Weak Preferences

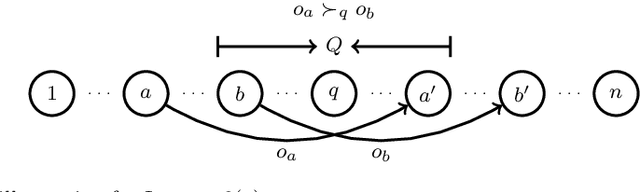
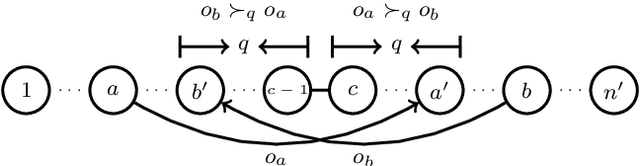
The \textsc{Housing Market} problem is a widely studied resource allocation problem. In this problem, each agent can only receive a single object and has preferences over all objects. Starting from an initial endowment, we want to reach a certain assignment via a sequence of rational trades. We first consider whether an object is reachable for a given agent under a social network, where a trade between two agents is allowed if they are neighbors in the network and no participant has a deficit from the trade. Assume that the preferences of the agents are strict (no tie among objects is allowed). This problem is polynomially solvable in a star-network and NP-complete in a tree-network. It is left as a challenging open problem whether the problem is polynomially solvable when the network is a path. We answer this open problem positively by giving a polynomial-time algorithm. Then we show that when the preferences of the agents are weak (ties among objects are allowed), the problem becomes NP-hard even when the network is a path. In addition, we consider the computational complexity of finding different optimal assignments for the problem under the network being a path or a star.