A Fast Maximum $k$-Plex Algorithm Parameterized by the Degeneracy Gap
Paper and Code
Jun 23, 2023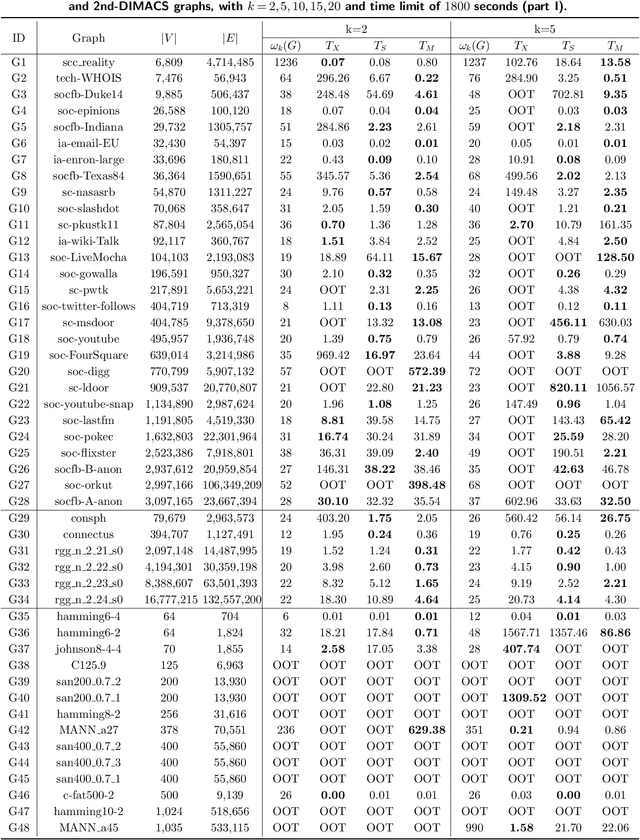
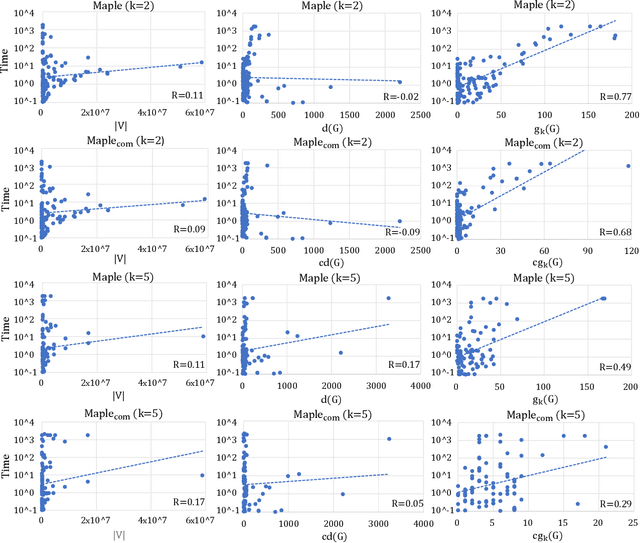
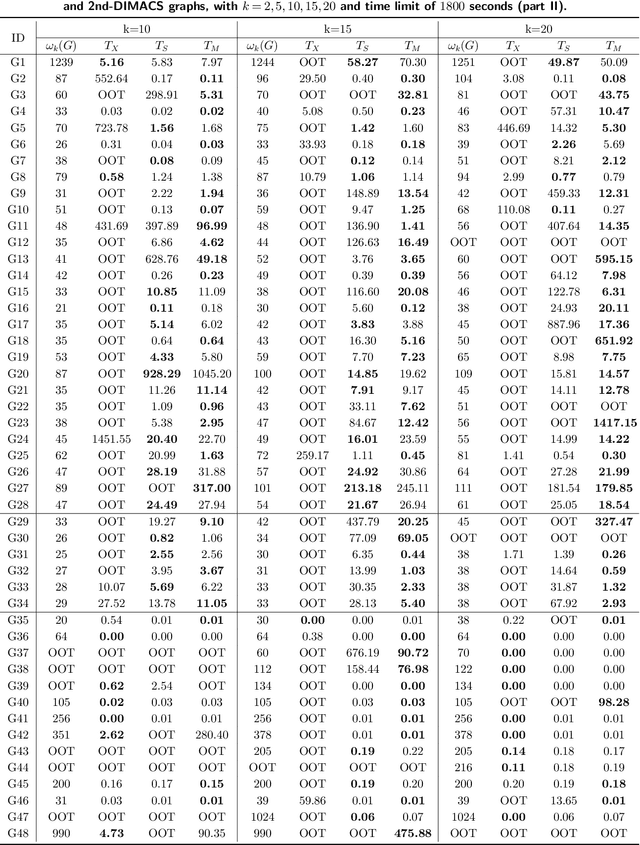
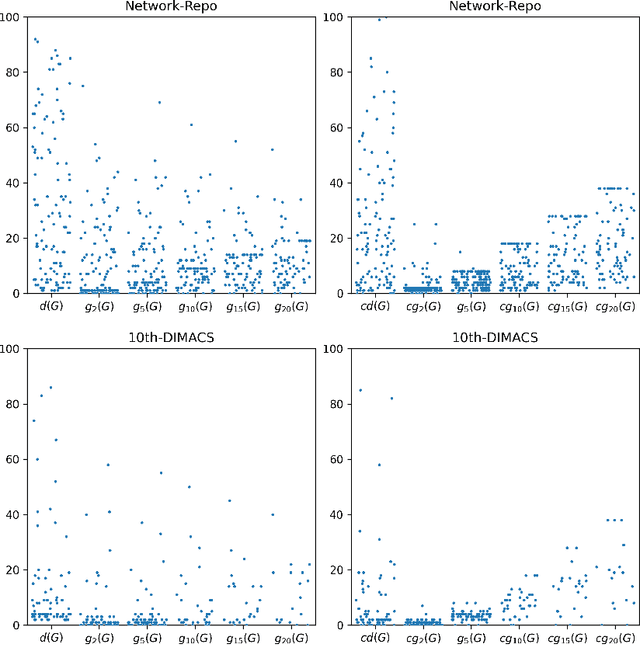
Given a graph, the $k$-plex is a vertex set in which each vertex is not adjacent to at most $k-1$ other vertices in the set. The maximum $k$-plex problem, which asks for the largest $k$-plex from a given graph, is an important but computationally challenging problem in applications like graph search and community detection. So far, there is a number of empirical algorithms without sufficient theoretical explanations on the efficiency. We try to bridge this gap by defining a novel parameter of the input instance, $g_k(G)$, the gap between the degeneracy bound and the size of maximum $k$-plex in the given graph, and presenting an exact algorithm parameterized by $g_k(G)$. In other words, we design an algorithm with running time polynomial in the size of input graph and exponential in $g_k(G)$ where $k$ is a constant. Usually, $g_k(G)$ is small and bounded by $O(\log{(|V|)})$ in real-world graphs, indicating that the algorithm runs in polynomial time. We also carry out massive experiments and show that the algorithm is competitive with the state-of-the-art solvers. Additionally, for large $k$ values such as $15$ and $20$, our algorithm has superior performance over existing algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge