A Faster Branching Algorithm for the Maximum $k$-Defective Clique Problem

A $k$-defective clique of an undirected graph $G$ is a subset of its vertices that induces a nearly complete graph with a maximum of $k$ missing edges. The maximum $k$-defective clique problem, which asks for the largest $k$-defective clique from the given graph, is important in many applications, such as social and biological network analysis. In the paper, we propose a new branching algorithm that takes advantage of the structural properties of the $k$-defective clique and uses the efficient maximum clique algorithm as a subroutine. As a result, the algorithm has a better asymptotic running time than the existing ones. We also investigate upper-bounding techniques and propose a new upper bound utilizing the \textit{conflict relationship} between vertex pairs. Because conflict relationship is common in many graph problems, we believe that this technique can be potentially generalized. Finally, experiments show that our algorithm outperforms state-of-the-art solvers on a wide range of open benchmarks.

A Fast Maximum $k$-Plex Algorithm Parameterized by the Degeneracy Gap

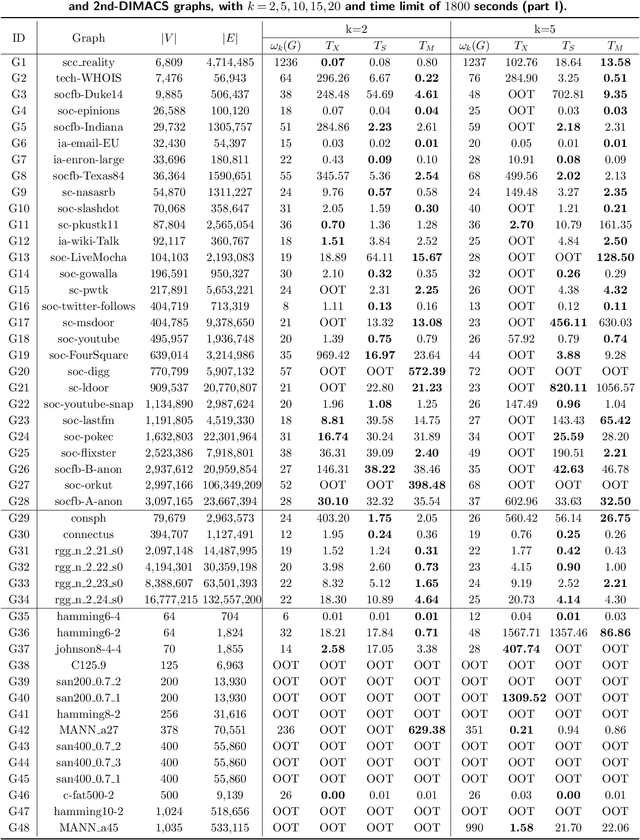
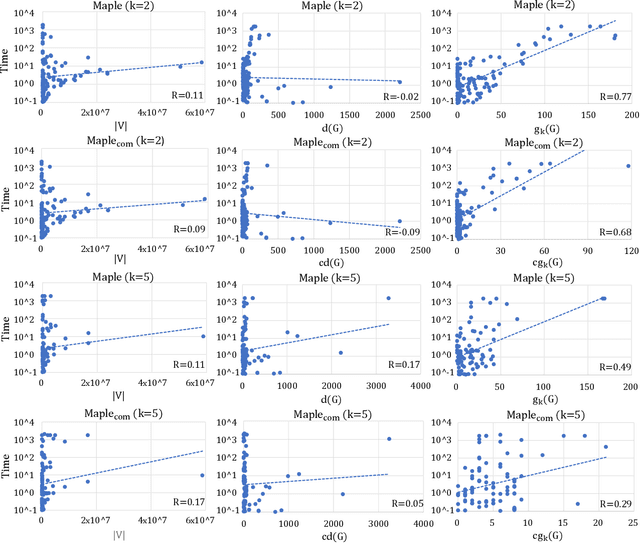
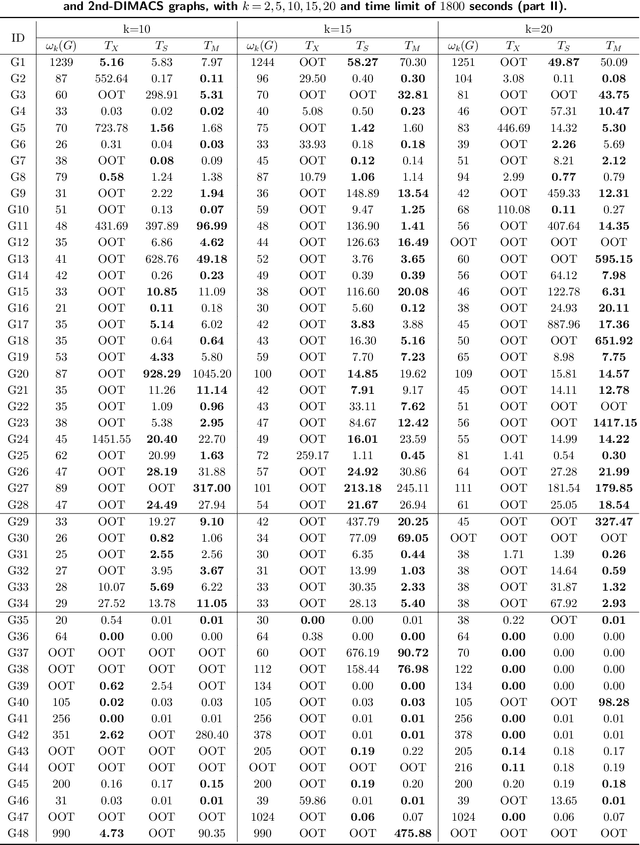
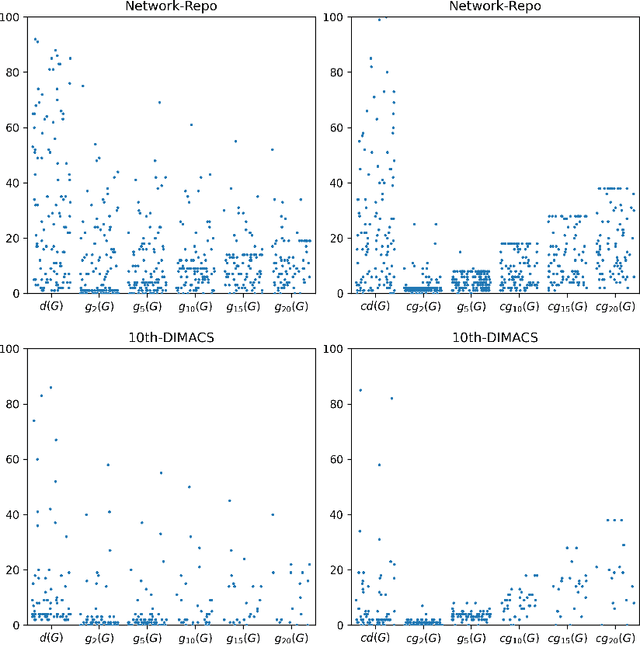
Given a graph, the $k$-plex is a vertex set in which each vertex is not adjacent to at most $k-1$ other vertices in the set. The maximum $k$-plex problem, which asks for the largest $k$-plex from a given graph, is an important but computationally challenging problem in applications like graph search and community detection. So far, there is a number of empirical algorithms without sufficient theoretical explanations on the efficiency. We try to bridge this gap by defining a novel parameter of the input instance, $g_k(G)$, the gap between the degeneracy bound and the size of maximum $k$-plex in the given graph, and presenting an exact algorithm parameterized by $g_k(G)$. In other words, we design an algorithm with running time polynomial in the size of input graph and exponential in $g_k(G)$ where $k$ is a constant. Usually, $g_k(G)$ is small and bounded by $O(\log{(|V|)})$ in real-world graphs, indicating that the algorithm runs in polynomial time. We also carry out massive experiments and show that the algorithm is competitive with the state-of-the-art solvers. Additionally, for large $k$ values such as $15$ and $20$, our algorithm has superior performance over existing algorithms.