Listing Maximal k-Plexes in Large Real-World Graphs

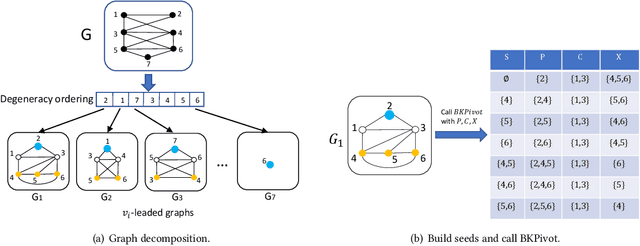
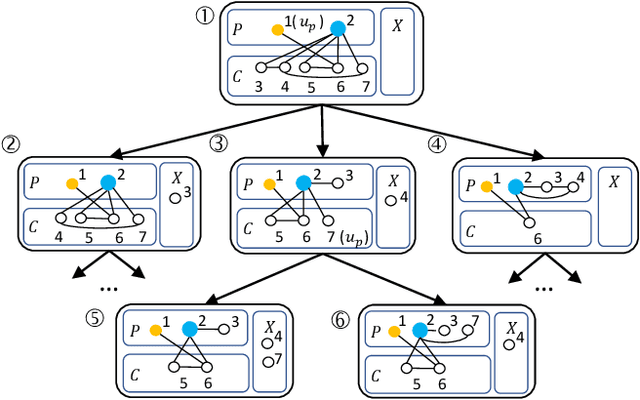
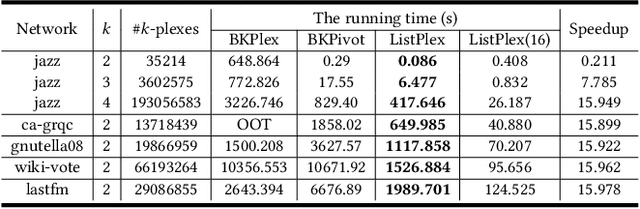
Listing dense subgraphs in large graphs plays a key task in varieties of network analysis applications like community detection. Clique, as the densest model, has been widely investigated. However, in practice, communities rarely form as cliques for various reasons, e.g., data noise. Therefore, $k$-plex, -- graph with each vertex adjacent to all but at most $k$ vertices, is introduced as a relaxed version of clique. Often, to better simulate cohesive communities, an emphasis is placed on connected $k$-plexes with small $k$. In this paper, we continue the research line of listing all maximal $k$-plexes and maximal $k$-plexes of prescribed size. Our first contribution is algorithm ListPlex that lists all maximal $k$-plexes in $O^*(\gamma^D)$ time for each constant $k$, where $\gamma$ is a value related to $k$ but strictly smaller than 2, and $D$ is the degeneracy of the graph that is far less than the vertex number $n$ in real-word graphs. Compared to the trivial bound of $2^n$, the improvement is significant, and our bound is better than all previously known results. In practice, we further use several techniques to accelerate listing $k$-plexes of a given size, such as structural-based prune rules, cache-efficient data structures, and parallel techniques. All these together result in a very practical algorithm. Empirical results show that our approach outperforms the state-of-the-art solutions by up to orders of magnitude.

Agent-Level Maximum Entropy Inverse Reinforcement Learning for Mean Field Games

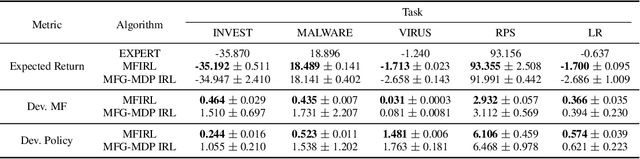
Mean field games (MFG) facilitate the application of reinforcement learning (RL) in large-scale multi-agent systems, through reducing interplays among agents to those between an individual agent and the average effect from the population. However, RL agents are notoriously prone to unexpected behaviours due to the reward mis-specification. Although inverse RL (IRL) holds promise for automatically acquiring suitable rewards from demonstrations, its extension to MFG is challenging due to the complicated notion of mean-field-type equilibria and the coupling between agent-level and population-level dynamics. To this end, we propose a novel IRL framework for MFG, called Mean Field IRL (MFIRL), where we build upon a new equilibrium concept and the maximum entropy IRL framework. Crucially, MFIRL is brought forward as the first IRL method that can recover the agent-level (ground-truth) reward functions for MFG. Experiments show the superior performance of MFIRL on sample efficiency, reward recovery and robustness against varying environment dynamics, compared to the state-of-the-art method.