Agent-Level Maximum Entropy Inverse Reinforcement Learning for Mean Field Games
Paper and Code
May 30, 2021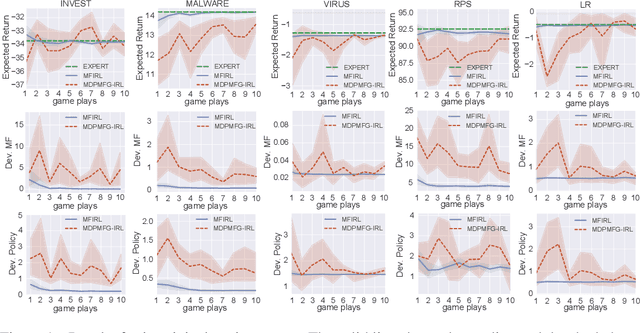
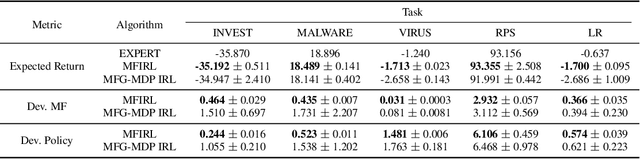
Mean field games (MFG) facilitate the application of reinforcement learning (RL) in large-scale multi-agent systems, through reducing interplays among agents to those between an individual agent and the average effect from the population. However, RL agents are notoriously prone to unexpected behaviours due to the reward mis-specification. Although inverse RL (IRL) holds promise for automatically acquiring suitable rewards from demonstrations, its extension to MFG is challenging due to the complicated notion of mean-field-type equilibria and the coupling between agent-level and population-level dynamics. To this end, we propose a novel IRL framework for MFG, called Mean Field IRL (MFIRL), where we build upon a new equilibrium concept and the maximum entropy IRL framework. Crucially, MFIRL is brought forward as the first IRL method that can recover the agent-level (ground-truth) reward functions for MFG. Experiments show the superior performance of MFIRL on sample efficiency, reward recovery and robustness against varying environment dynamics, compared to the state-of-the-art method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge