Systematic Parameter Decision in Approximate Model Counting

This paper proposes a novel approach to determining the internal parameters of the hashing-based approximate model counting algorithm $\mathsf{ApproxMC}$. In this problem, the chosen parameter values must ensure that $\mathsf{ApproxMC}$ is Probably Approximately Correct (PAC), while also making it as efficient as possible. The existing approach to this problem relies on heuristics; in this paper, we solve this problem by formulating it as an optimization problem that arises from generalizing $\mathsf{ApproxMC}$'s correctness proof to arbitrary parameter values. Our approach separates the concerns of algorithm soundness and optimality, allowing us to address the former without the need for repetitive case-by-case argumentation, while establishing a clear framework for the latter. Furthermore, after reduction, the resulting optimization problem takes on an exceptionally simple form, enabling the use of a basic search algorithm and providing insight into how parameter values affect algorithm performance. Experimental results demonstrate that our optimized parameters improve the runtime performance of the latest $\mathsf{ApproxMC}$ by a factor of 1.6 to 2.4, depending on the error tolerance.

Learning Density-Based Correlated Equilibria for Markov Games

Correlated Equilibrium (CE) is a well-established solution concept that captures coordination among agents and enjoys good algorithmic properties. In real-world multi-agent systems, in addition to being in an equilibrium, agents' policies are often expected to meet requirements with respect to safety, and fairness. Such additional requirements can often be expressed in terms of the state density which measures the state-visitation frequencies during the course of a game. However, existing CE notions or CE-finding approaches cannot explicitly specify a CE with particular properties concerning state density; they do so implicitly by either modifying reward functions or using value functions as the selection criteria. The resulting CE may thus not fully fulfil the state-density requirements. In this paper, we propose Density-Based Correlated Equilibria (DBCE), a new notion of CE that explicitly takes state density as selection criterion. Concretely, we instantiate DBCE by specifying different state-density requirements motivated by real-world applications. To compute DBCE, we put forward the Density Based Correlated Policy Iteration algorithm for the underlying control problem. We perform experiments on various games where results demonstrate the advantage of our CE-finding approach over existing methods in scenarios with state-density concerns.

Dynamic Shielding for Reinforcement Learning in Black-Box Environments

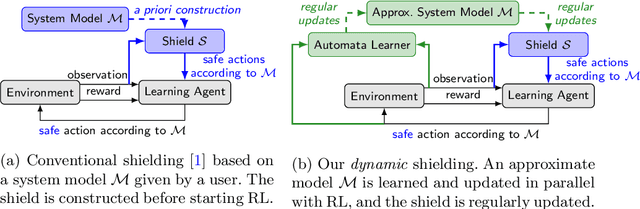
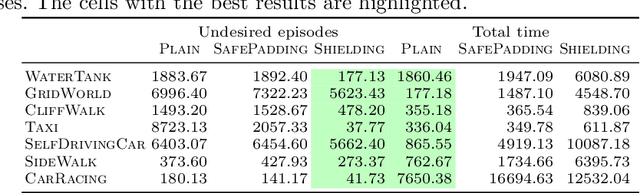
It is challenging to use reinforcement learning (RL) in cyber-physical systems due to the lack of safety guarantees during learning. Although there have been various proposals to reduce undesired behaviors during learning, most of these techniques require prior system knowledge, and their applicability is limited. This paper aims to reduce undesired behaviors during learning without requiring any prior system knowledge. We propose dynamic shielding: an extension of a model-based safe RL technique called shielding using automata learning. The dynamic shielding technique constructs an approximate system model in parallel with RL using a variant of the RPNI algorithm and suppresses undesired explorations due to the shield constructed from the learned model. Through this combination, potentially unsafe actions can be foreseen before the agent experiences them. Experiments show that our dynamic shield significantly decreases the number of undesired events during training.