Learning and Sequencing of Object-Centric Manipulation Skills for Industrial Tasks

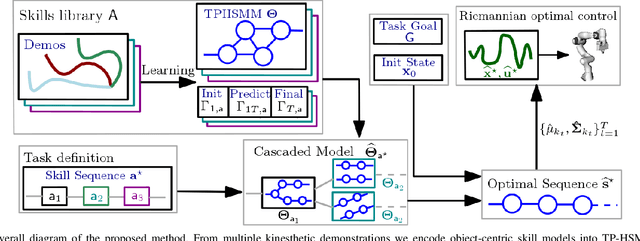
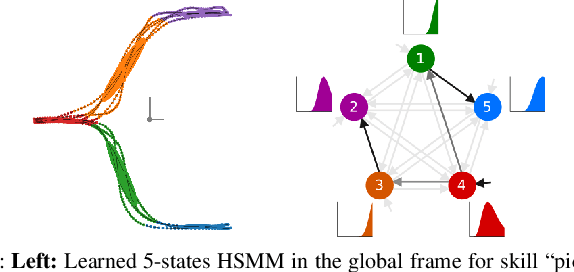
Enabling robots to quickly learn manipulation skills is an important, yet challenging problem. Such manipulation skills should be flexible, e.g., be able adapt to the current workspace configuration. Furthermore, to accomplish complex manipulation tasks, robots should be able to sequence several skills and adapt them to changing situations. In this work, we propose a rapid robot skill-sequencing algorithm, where the skills are encoded by object-centric hidden semi-Markov models. The learned skill models can encode multimodal (temporal and spatial) trajectory distributions. This approach significantly reduces manual modeling efforts, while ensuring a high degree of flexibility and re-usability of learned skills. Given a task goal and a set of generic skills, our framework computes smooth transitions between skill instances. To compute the corresponding optimal end-effector trajectory in task space we rely on Riemannian optimal controller. We demonstrate this approach on a 7 DoF robot arm for industrial assembly tasks.

A Projection Approach to Equality Constrained Iterative Linear Quadratic Optimal Control

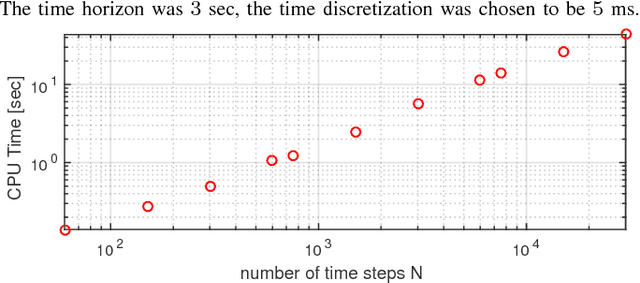
This paper presents a state and state-input constrained variant of the discrete-time iterative Linear Quadratic Regulator (iLQR) algorithm, with linear time-complexity in the number of time steps. The approach is based on a projection of the control input onto the nullspace of the linearized constraints. We derive a fully constraint-compliant feedforward-feedback control update rule, for which we can solve efficiently with Riccati-style difference equations. We assume that the relative degree of all constraints in the discrete-time system model is equal to one, which often holds for robotics problems employing rigid-body dynamic models. Simulation examples, including a 6 DoF robotic arm, are given to validate and illustrate the performance of the method.

The Control Toolbox - An Open-Source C++ Library for Robotics, Optimal and Model Predictive Control

We introduce the Control Toolbox (CT), an open-source C++ library for efficient modeling, control, estimation, trajectory optimization and Model Predictive Control. The CT is applicable to a broad class of dynamic systems but features interfaces to modeling tools specifically designed for robotic applications. This paper outlines the general concept of the toolbox, its main building blocks, and highlights selected application examples. The library contains several tools to design and evaluate controllers, model dynamical systems and solve optimal control problems. The CT was designed for intuitive modeling of systems governed by ordinary differential or difference equations. It supports rapid prototyping of cost functions and constraints and provides standard interfaces for different optimal control solvers. To date, we support Single Shooting, the iterative Linear-Quadratic Regulator, Gauss-Newton Multiple Shooting and classical Direct Multiple Shooting. We provide interfaces to general purpose NLP solvers and Riccati-based linear-quadratic optimal control solvers. The CT was designed to solve large-scale optimal control and estimation problems efficiently and allows for online control of dynamic systems. Some of the key features to enable fast run-time performance are full compatibility with Automatic Differentiation, derivative code generation, and multi-threading. Still, the CT is designed as a modular framework whose building blocks can also be used for other control and estimation applications such as inverse dynamics control, extended Kalman filters or kinematic planning.

Efficient Kinematic Planning for Mobile Manipulators with Non-holonomic Constraints Using Optimal Control

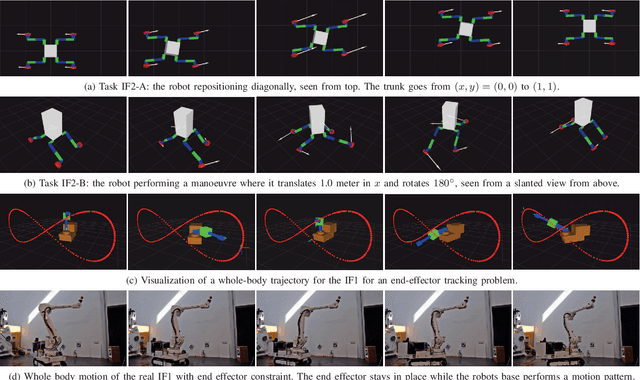
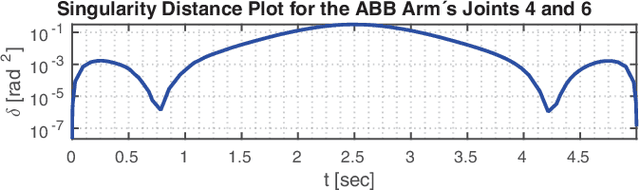
This work addresses the problem of kinematic trajectory planning for mobile manipulators with non-holonomic constraints, and holonomic operational-space tracking constraints. We obtain whole-body trajectories and time-varying kinematic feedback controllers by solving a Constrained Sequential Linear Quadratic Optimal Control problem. The employed algorithm features high efficiency through a continuous-time formulation that benefits from adaptive step-size integrators and through linear complexity in the number of integration steps. In a first application example, we solve kinematic trajectory planning problems for a 26 DoF wheeled robot. In a second example, we apply Constrained SLQ to a real-world mobile manipulator in a receding-horizon optimal control fashion, where we obtain optimal controllers and plans at rates up to 100 Hz.

Automatic Differentiation of Rigid Body Dynamics for Optimal Control and Estimation

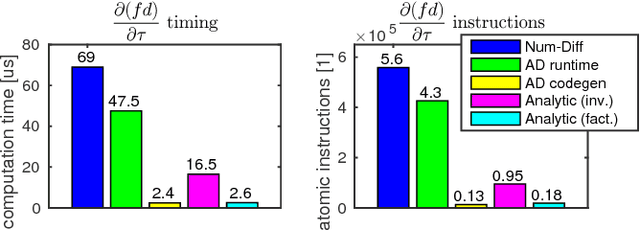
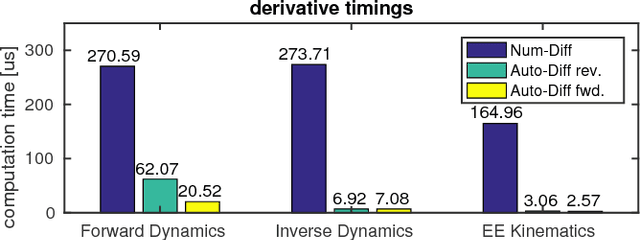
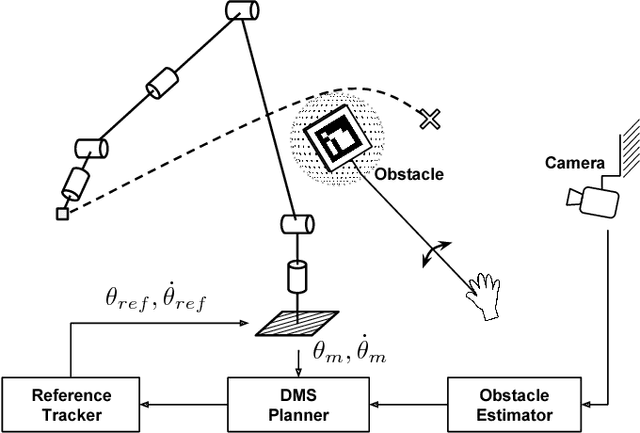
Many algorithms for control, optimization and estimation in robotics depend on derivatives of the underlying system dynamics, e.g. to compute linearizations, sensitivities or gradient directions. However, we show that when dealing with Rigid Body Dynamics, these derivatives are difficult to derive analytically and to implement efficiently. To overcome this issue, we extend the modelling tool `RobCoGen' to be compatible with Automatic Differentiation. Additionally, we propose how to automatically obtain the derivatives and generate highly efficient source code. We highlight the flexibility and performance of the approach in two application examples. First, we show a Trajectory Optimization example for the quadrupedal robot HyQ, which employs auto-differentiation on the dynamics including a contact model. Second, we present a hardware experiment in which a 6 DoF robotic arm avoids a randomly moving obstacle in a go-to task by fast, dynamic replanning.

A Family of Iterative Gauss-Newton Shooting Methods for Nonlinear Optimal Control

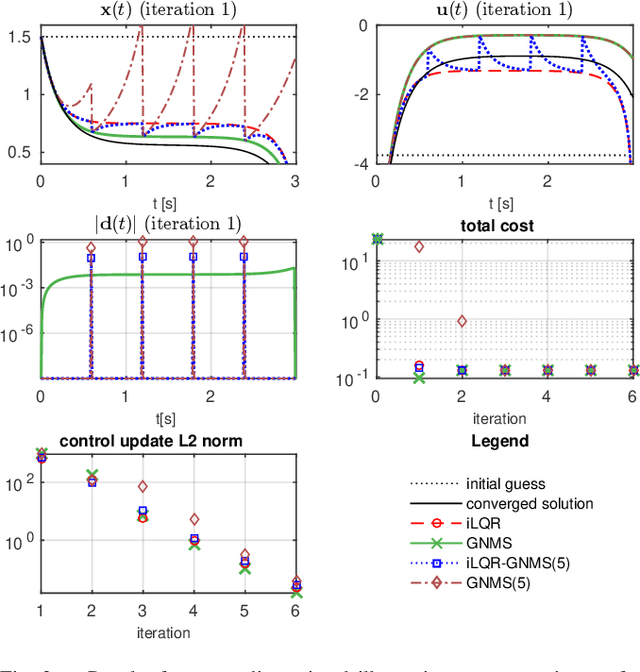
This paper introduces a family of iterative algorithms for unconstrained nonlinear optimal control. We generalize the well-known iLQR algorithm to different multiple-shooting variants, combining advantages like straight-forward initialization and a closed-loop forward integration. All algorithms have similar computational complexity, i.e. linear complexity in the time horizon, and can be derived in the same computational framework. We compare the full-step variants of our algorithms and present several simulation examples, including a high-dimensional underactuated robot subject to contact switches. Simulation results show that our multiple-shooting algorithms can achieve faster convergence, better local contraction rates and much shorter runtimes than classical iLQR, which makes them a superior choice for nonlinear model predictive control applications.

Whole-Body Nonlinear Model Predictive Control Through Contacts for Quadrupeds

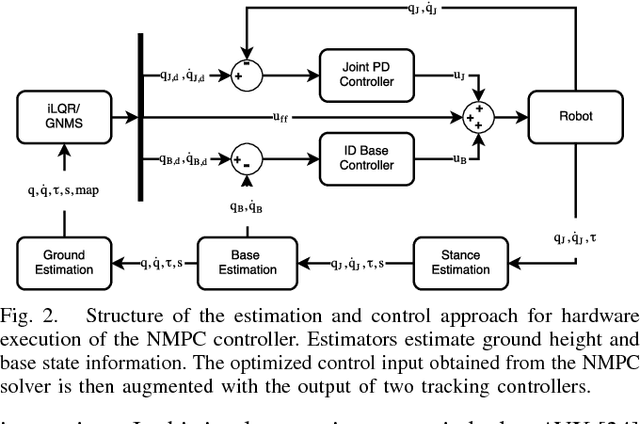
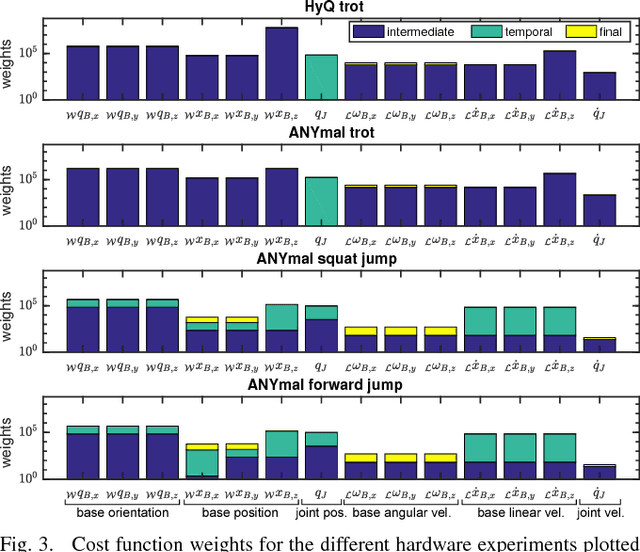
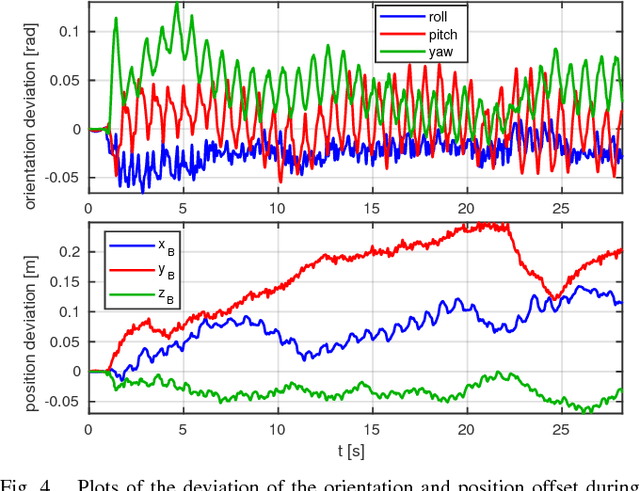
In this work we present a whole-body Nonlinear Model Predictive Control approach for Rigid Body Systems subject to contacts. We use a full dynamic system model which also includes explicit contact dynamics. Therefore, contact locations, sequences and timings are not prespecified but optimized by the solver. Yet, thorough numerical and software engineering allows for running the nonlinear Optimal Control solver at rates up to 190 Hz on a quadruped for a time horizon of half a second. This outperforms the state of the art by at least one order of magnitude. Hardware experiments in form of periodic and non-periodic tasks are applied to two quadrupeds with different actuation systems. The obtained results underline the performance, transferability and robustness of the approach.

Real-Time Motion Planning of Legged Robots: A Model Predictive Control Approach

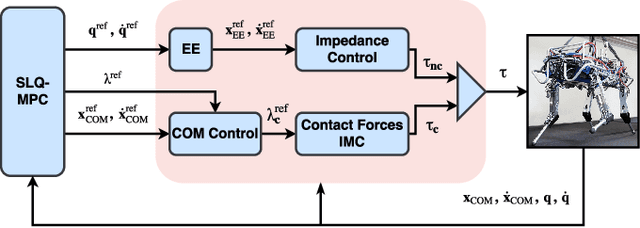
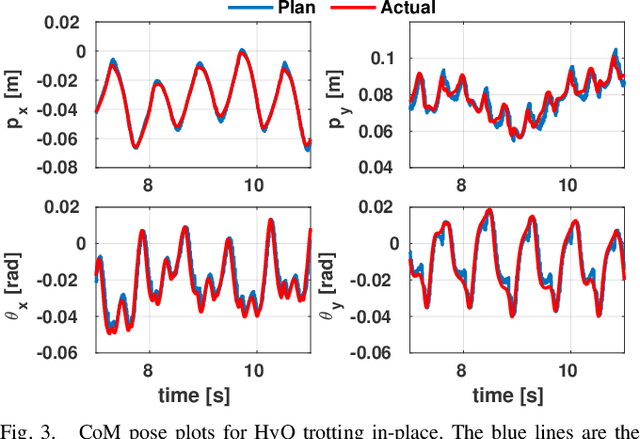
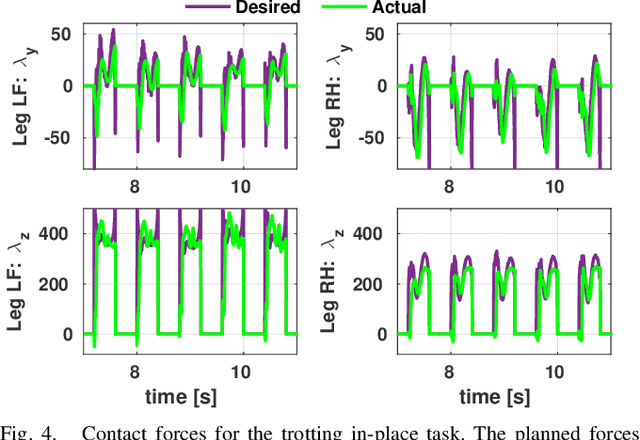
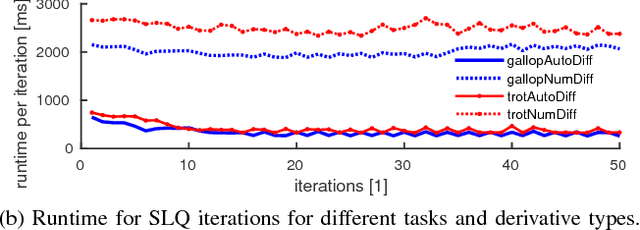
We introduce a real-time, constrained, nonlinear Model Predictive Control for the motion planning of legged robots. The proposed approach uses a constrained optimal control algorithm known as SLQ. We improve the efficiency of this algorithm by introducing a multi-processing scheme for estimating value function in its backward pass. This pass has been often calculated as a single process. This parallel SLQ algorithm can optimize longer time horizons without proportional increase in its computation time. Thus, our MPC algorithm can generate optimized trajectories for the next few phases of the motion within only a few milliseconds. This outperforms the state of the art by at least one order of magnitude. The performance of the approach is validated on a quadruped robot for generating dynamic gaits such as trotting.

Optimal and Learning Control for Autonomous Robots

Optimal and Learning Control for Autonomous Robots has been taught in the Robotics, Systems and Controls Masters at ETH Zurich with the aim to teach optimal control and reinforcement learning for closed loop control problems from a unified point of view. The starting point is the formulation of of an optimal control problem and deriving the different types of solutions and algorithms from there. These lecture notes aim at supporting this unified view with a unified notation wherever possible, and a bit of a translation help to compare the terminology and notation in the different fields. The course assumes basic knowledge of Control Theory, Linear Algebra and Stochastic Calculus.

Mobile Robotic Fabrication at 1:1 scale: the In situ Fabricator

This paper presents the concept of an In situ Fabricator, a mobile robot intended for on-site manufacturing, assembly and digital fabrication. We present an overview of a prototype system, its capabilities, and highlight the importance of high-performance control, estimation and planning algorithms for achieving desired construction goals. Next, we detail on two architectural application scenarios: first, building a full-size undulating brick wall, which required a number of repositioning and autonomous localisation manoeuvres. Second, the Mesh Mould concrete process, which shows that an In situ Fabricator in combination with an innovative digital fabrication tool can be used to enable completely novel building technologies. Subsequently, important limitations and disadvantages of our approach are discussed. Based on that, we identify the need for a new type of robotic actuator, which facilitates the design of novel full-scale construction robots. We provide brief insight into the development of this actuator and conclude the paper with an outlook on the next-generation In situ Fabricator, which is currently under development.