GRIP: In-Parameter Graph Reasoning through Fine-Tuning Large Language Models

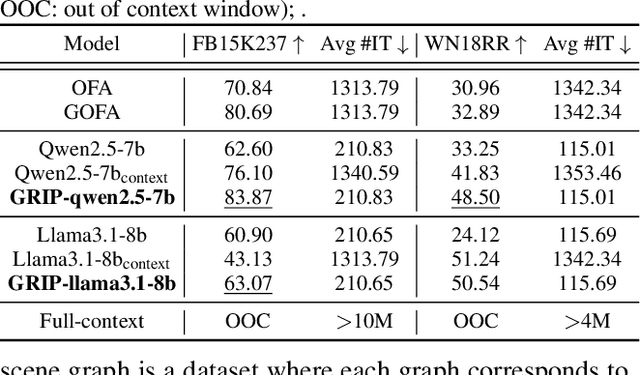
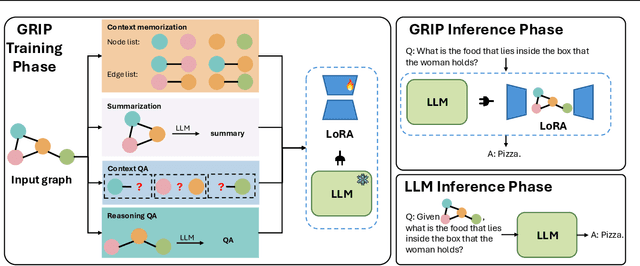
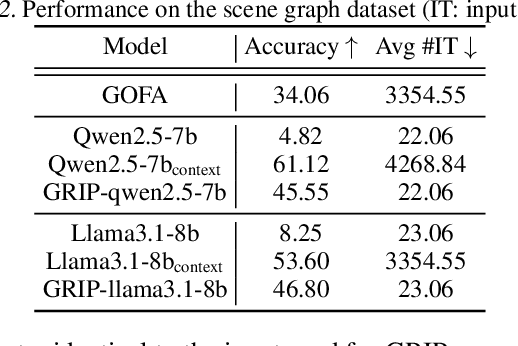
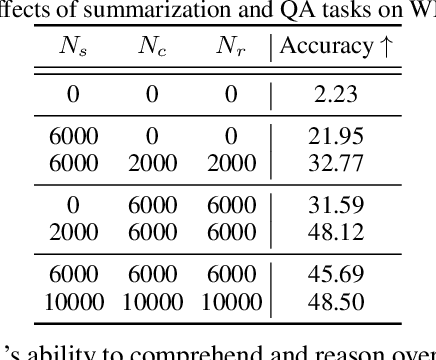
Large Language Models (LLMs) have demonstrated remarkable capabilities in modeling sequential textual data and generalizing across diverse tasks. However, adapting LLMs to effectively handle structural data, such as knowledge graphs or web data, remains a challenging problem. Some approaches adopt complex strategies to convert graphs into text sequences, resulting in significant token overhead and rendering them impractical for large-scale graphs. Others introduce additional modules to encode graphs into fixed-size token representations for LLMs. However, these methods typically require large-scale post-training on graph-text corpus and complex alignment procedures, yet often yield sub-optimal results due to poor modality alignment. Inspired by in-parameter knowledge injection for test-time adaptation of LLMs, we propose GRIP, a novel framework that equips LLMs with the ability to internalize complex relational information from graphs through carefully designed fine-tuning tasks. This knowledge is efficiently stored within lightweight LoRA parameters, enabling the fine-tuned LLM to perform a wide range of graph-related tasks without requiring access to the original graph at inference time. Extensive experiments across multiple benchmarks validate the effectiveness and efficiency of our approach.

Addressing accuracy and hallucination of LLMs in Alzheimer's disease research through knowledge graphs

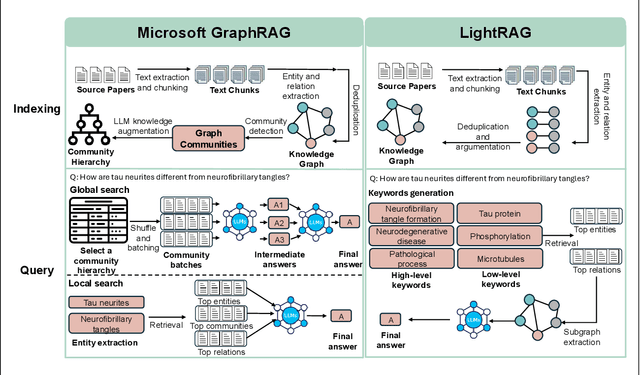
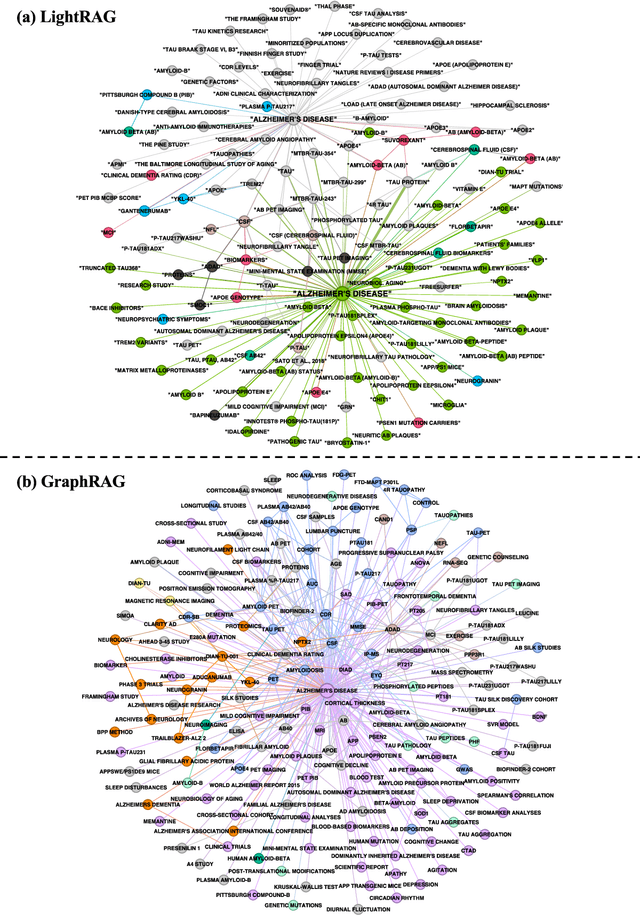
In the past two years, large language model (LLM)-based chatbots, such as ChatGPT, have revolutionized various domains by enabling diverse task completion and question-answering capabilities. However, their application in scientific research remains constrained by challenges such as hallucinations, limited domain-specific knowledge, and lack of explainability or traceability for the response. Graph-based Retrieval-Augmented Generation (GraphRAG) has emerged as a promising approach to improving chatbot reliability by integrating domain-specific contextual information before response generation, addressing some limitations of standard LLMs. Despite its potential, there are only limited studies that evaluate GraphRAG on specific domains that require intensive knowledge, like Alzheimer's disease or other biomedical domains. In this paper, we assess the quality and traceability of two popular GraphRAG systems. We compile a database of 50 papers and 70 expert questions related to Alzheimer's disease, construct a GraphRAG knowledge base, and employ GPT-4o as the LLM for answering queries. We then compare the quality of responses generated by GraphRAG with those from a standard GPT-4o model. Additionally, we discuss and evaluate the traceability of several Retrieval-Augmented Generation (RAG) and GraphRAG systems. Finally, we provide an easy-to-use interface with a pre-built Alzheimer's disease database for researchers to test the performance of both standard RAG and GraphRAG.

GOFA: A Generative One-For-All Model for Joint Graph Language Modeling

Foundation models, such as Large Language Models (LLMs) or Large Vision Models (LVMs), have emerged as one of the most powerful tools in the respective fields. However, unlike text and image data, graph data do not have a definitive structure, posing great challenges to developing a Graph Foundation Model (GFM). For example, current attempts at designing general graph models either transform graph data into a language format for LLM-based prediction or still train a GNN model with LLM as an assistant. The former can handle unlimited tasks, while the latter captures graph structure much better -- yet, no existing work can achieve both simultaneously. In this paper, we identify three key desirable properties of a GFM: self-supervised pretraining, fluidity in tasks, and graph awareness. To account for these properties, we extend the conventional language modeling to the graph domain and propose a novel generative graph language model GOFA to solve the problem. The model interleaves randomly initialized GNN layers into a frozen pre-trained LLM so that the semantic and structural modeling abilities are organically combined. GOFA is pre-trained on newly proposed graph-level next-word prediction, question-answering, and structural tasks to obtain the above GFM properties. The pre-trained model is further fine-tuned on downstream tasks to obtain task-solving ability. The fine-tuned model is evaluated on various downstream tasks, demonstrating a strong ability to solve structural and contextual problems in zero-shot scenarios. The code is available at https://github.com/JiaruiFeng/GOFA.

TAGLAS: An atlas of text-attributed graph datasets in the era of large graph and language models

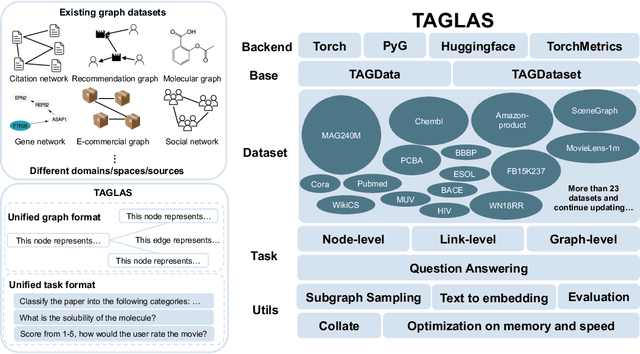
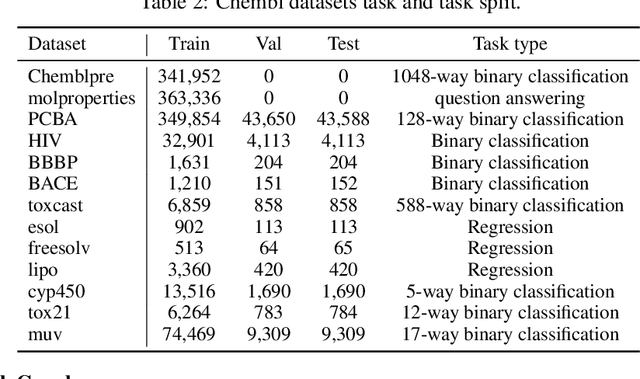
In this report, we present TAGLAS, an atlas of text-attributed graph (TAG) datasets and benchmarks. TAGs are graphs with node and edge features represented in text, which have recently gained wide applicability in training graph-language or graph foundation models. In TAGLAS, we collect and integrate more than 23 TAG datasets with domains ranging from citation graphs to molecule graphs and tasks from node classification to graph question-answering. Unlike previous graph datasets and benchmarks, all datasets in TAGLAS have a unified node and edge text feature format, which allows a graph model to be simultaneously trained and evaluated on multiple datasets from various domains. Further, we provide a standardized, efficient, and simplified way to load all datasets and tasks. We also provide useful utils like text-to-embedding conversion, and graph-to-text conversion, which can facilitate different evaluation scenarios. Finally, we also provide standard and easy-to-use evaluation utils. The project is open-sourced at https://github.com/JiaruiFeng/TAGLAS and is still under construction. Please expect more datasets/features in the future.

Can Graph Learning Improve Task Planning?

Task planning is emerging as an important research topic alongside the development of large language models (LLMs). It aims to break down complex user requests into solvable sub-tasks, thereby fulfilling the original requests. In this context, the sub-tasks can be naturally viewed as a graph, where the nodes represent the sub-tasks, and the edges denote the dependencies among them. Consequently, task planning is a decision-making problem that involves selecting a connected path or subgraph within the corresponding graph and invoking it. In this paper, we explore graph learning-based methods for task planning, a direction that is orthogonal to the prevalent focus on prompt design. Our interest in graph learning stems from a theoretical discovery: the biases of attention and auto-regressive loss impede LLMs' ability to effectively navigate decision-making on graphs, which is adeptly addressed by graph neural networks (GNNs). This theoretical insight led us to integrate GNNs with LLMs to enhance overall performance. Extensive experiments demonstrate that GNN-based methods surpass existing solutions even without training, and minimal training can further enhance their performance. Additionally, our approach complements prompt engineering and fine-tuning techniques, with performance further enhanced by improved prompts or a fine-tuned model.

MAG-GNN: Reinforcement Learning Boosted Graph Neural Network

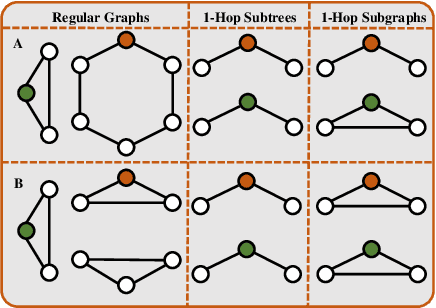
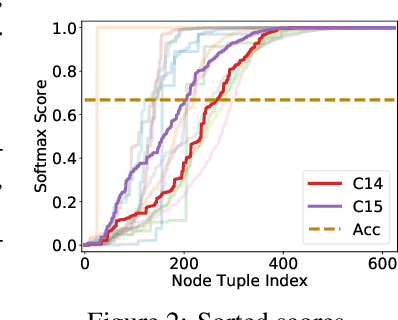
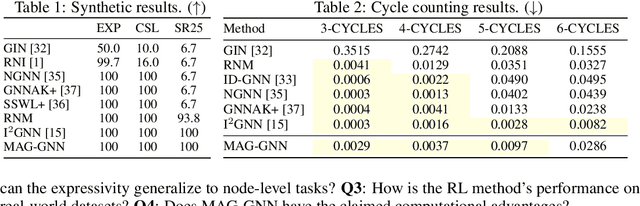
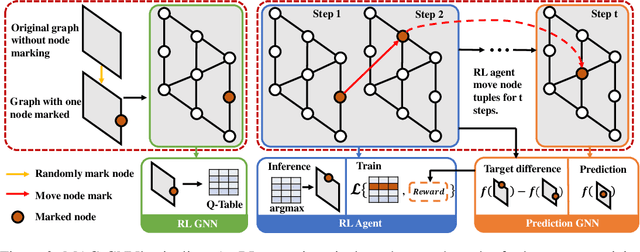
While Graph Neural Networks (GNNs) recently became powerful tools in graph learning tasks, considerable efforts have been spent on improving GNNs' structural encoding ability. A particular line of work proposed subgraph GNNs that use subgraph information to improve GNNs' expressivity and achieved great success. However, such effectivity sacrifices the efficiency of GNNs by enumerating all possible subgraphs. In this paper, we analyze the necessity of complete subgraph enumeration and show that a model can achieve a comparable level of expressivity by considering a small subset of the subgraphs. We then formulate the identification of the optimal subset as a combinatorial optimization problem and propose Magnetic Graph Neural Network (MAG-GNN), a reinforcement learning (RL) boosted GNN, to solve the problem. Starting with a candidate subgraph set, MAG-GNN employs an RL agent to iteratively update the subgraphs to locate the most expressive set for prediction. This reduces the exponential complexity of subgraph enumeration to the constant complexity of a subgraph search algorithm while keeping good expressivity. We conduct extensive experiments on many datasets, showing that MAG-GNN achieves competitive performance to state-of-the-art methods and even outperforms many subgraph GNNs. We also demonstrate that MAG-GNN effectively reduces the running time of subgraph GNNs.

One for All: Towards Training One Graph Model for All Classification Tasks

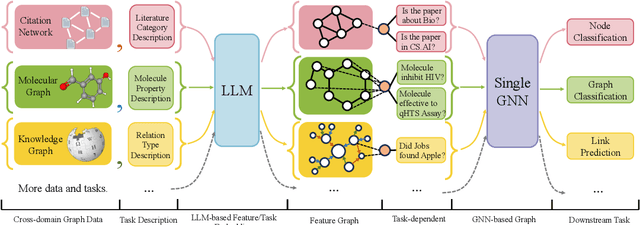
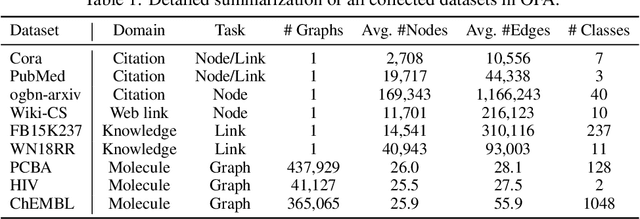
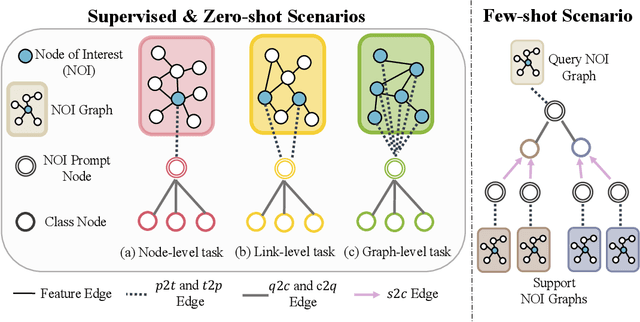
Designing a single model that addresses multiple tasks has been a long-standing objective in artificial intelligence. Recently, large language models have demonstrated exceptional capability in integrating and solving different tasks within the language domain. However, a unified model for various tasks on graphs remains underexplored, primarily due to the challenges unique to the graph learning domain. First, graph data from different areas carry distinct attributes and follow different distributions. Such discrepancy makes it hard to represent graphs in a single representation space. Second, tasks on graphs diversify into node, link, and graph tasks, requiring distinct embedding strategies. Finally, an appropriate graph prompting paradigm for in-context learning is unclear. Striving to handle all the aforementioned challenges, we propose One for All (OFA), the first general framework that can use a single graph model to address the above challenges. Specifically, OFA proposes text-attributed graphs to unify different graph data by describing nodes and edges with natural language and uses language models to encode the diverse and possibly cross-domain text attributes to feature vectors in the same embedding space. Furthermore, OFA introduces the concept of nodes-of-interest to standardize different tasks with a single task representation. For in-context learning on graphs, OFA introduces a novel graph prompting paradigm that appends prompting substructures to the input graph, which enables it to address varied tasks without fine-tuning. We train the OFA model using graph data from multiple domains (including citation networks, molecular graphs, knowledge graphs, etc.) simultaneously and evaluate its ability in supervised, few-shot, and zero-shot learning scenarios. OFA performs well across different tasks, making it the first general-purpose graph classification model across domains.

Graph Contrastive Learning Meets Graph Meta Learning: A Unified Method for Few-shot Node Tasks

Graph Neural Networks (GNNs) have become popular in Graph Representation Learning (GRL). One fundamental application is few-shot node classification. Most existing methods follow the meta learning paradigm, showing the ability of fast generalization to few-shot tasks. However, recent works indicate that graph contrastive learning combined with fine-tuning can significantly outperform meta learning methods. Despite the empirical success, there is limited understanding of the reasons behind it. In our study, we first identify two crucial advantages of contrastive learning compared to meta learning, including (1) the comprehensive utilization of graph nodes and (2) the power of graph augmentations. To integrate the strength of both contrastive learning and meta learning on the few-shot node classification tasks, we introduce a new paradigm: Contrastive Few-Shot Node Classification (COLA). Specifically, COLA employs graph augmentations to identify semantically similar nodes, which enables the construction of meta-tasks without the need for label information. Therefore, COLA can utilize all nodes to construct meta-tasks, further reducing the risk of overfitting. Through extensive experiments, we validate the essentiality of each component in our design and demonstrate that COLA achieves new state-of-the-art on all tasks.

Distance-Restricted Folklore Weisfeiler-Leman GNNs with Provable Cycle Counting Power

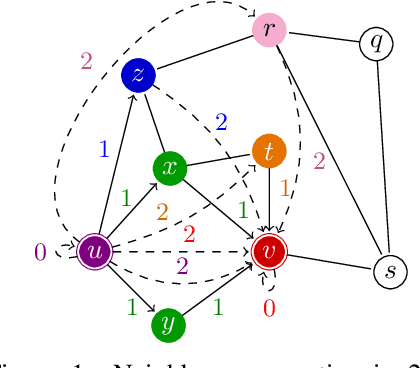
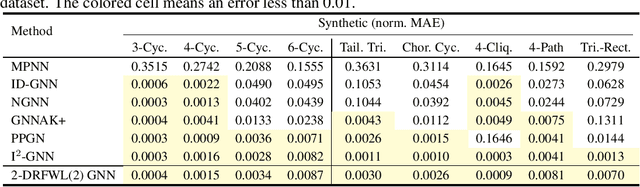
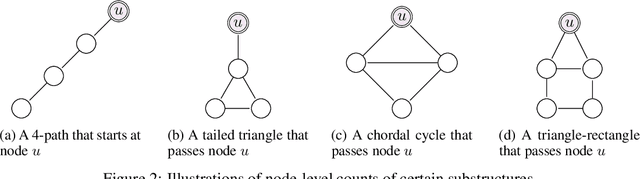
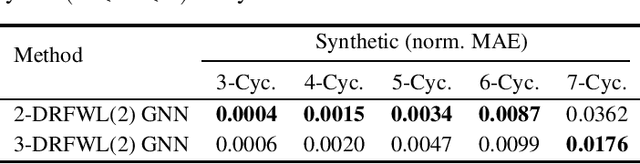
The ability of graph neural networks (GNNs) to count certain graph substructures, especially cycles, is important for the success of GNNs on a wide range of tasks. It has been recently used as a popular metric for evaluating the expressive power of GNNs. Many of the proposed GNN models with provable cycle counting power are based on subgraph GNNs, i.e., extracting a bag of subgraphs from the input graph, generating representations for each subgraph, and using them to augment the representation of the input graph. However, those methods require heavy preprocessing, and suffer from high time and memory costs. In this paper, we overcome the aforementioned limitations of subgraph GNNs by proposing a novel class of GNNs -- $d$-Distance-Restricted FWL(2) GNNs, or $d$-DRFWL(2) GNNs. $d$-DRFWL(2) GNNs use node pairs whose mutual distances are at most $d$ as the units for message passing to balance the expressive power and complexity. By performing message passing among distance-restricted node pairs in the original graph, $d$-DRFWL(2) GNNs avoid the expensive subgraph extraction operations in subgraph GNNs, making both the time and space complexity lower. We theoretically show that the discriminative power of $d$-DRFWL(2) GNNs strictly increases as $d$ increases. More importantly, $d$-DRFWL(2) GNNs have provably strong cycle counting power even with $d=2$: they can count all 3, 4, 5, 6-cycles. Since 6-cycles (e.g., benzene rings) are ubiquitous in organic molecules, being able to detect and count them is crucial for achieving robust and generalizable performance on molecular tasks. Experiments on both synthetic datasets and molecular datasets verify our theory. To the best of our knowledge, our model is the most efficient GNN model to date (both theoretically and empirically) that can count up to 6-cycles.

Towards Arbitrarily Expressive GNNs in $O(n^2)$ Space by Rethinking Folklore Weisfeiler-Lehman

Message passing neural networks (MPNNs) have emerged as the most popular framework of graph neural networks (GNNs) in recent years. However, their expressive power is limited by the 1-dimensional Weisfeiler-Lehman (1-WL) test. Some works are inspired by $k$-WL/FWL (Folklore WL) and design the corresponding neural versions. Despite the high expressive power, there are serious limitations in this line of research. In particular, (1) $k$-WL/FWL requires at least $O(n^k)$ space complexity, which is impractical for large graphs even when $k=3$; (2) The design space of $k$-WL/FWL is rigid, with the only adjustable hyper-parameter being $k$. To tackle the first limitation, we propose an extension, $(k, t)$-FWL. We theoretically prove that even if we fix the space complexity to $O(n^2)$ in $(k, t)$-FWL, we can construct an expressiveness hierarchy up to solving the graph isomorphism problem. To tackle the second problem, we propose $k$-FWL+, which considers any equivariant set as neighbors instead of all nodes, thereby greatly expanding the design space of $k$-FWL. Combining these two modifications results in a flexible and powerful framework $(k, t)$-FWL+. We demonstrate $(k, t)$-FWL+ can implement most existing models with matching expressiveness. We then introduce an instance of $(k,t)$-FWL+ called Neighborhood$^2$-FWL (N$^2$-FWL), which is practically and theoretically sound. We prove that N$^2$-FWL is no less powerful than 3-WL, can encode many substructures while only requiring $O(n^2)$ space. Finally, we design its neural version named N$^2$-GNN and evaluate its performance on various tasks. N$^2$-GNN achieves superior performance on almost all tasks, with record-breaking results on ZINC-Subset (0.059) and ZINC-Full (0.013), outperforming previous state-of-the-art results by 10.6% and 40.9%, respectively.