How Powerful are K-hop Message Passing Graph Neural Networks
Paper and Code
May 26, 2022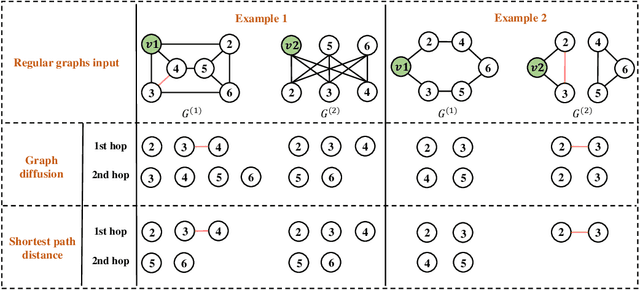
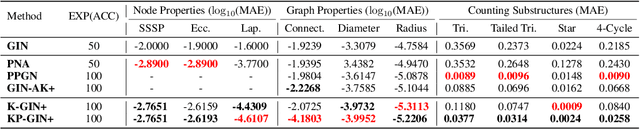
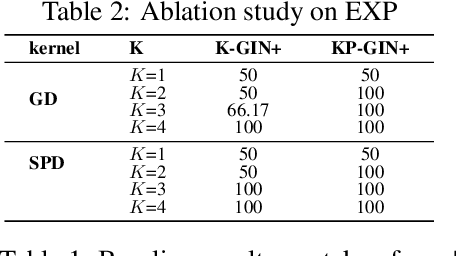
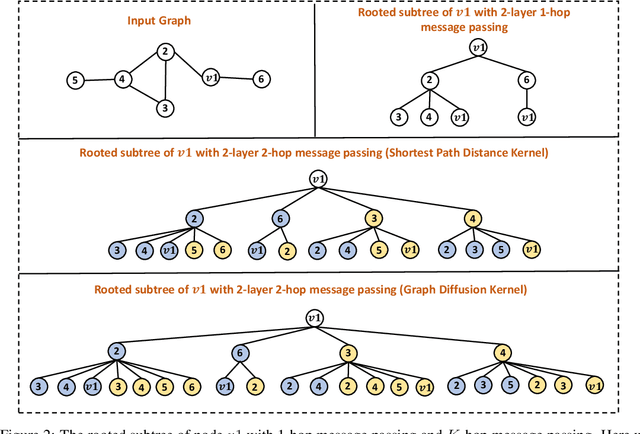
The most popular design paradigm for Graph Neural Networks (GNNs) is 1-hop message passing -- aggregating features from 1-hop neighbors repeatedly. However, the expressive power of 1-hop message passing is bounded by the Weisfeiler-Lehman (1-WL) test. Recently, researchers extended 1-hop message passing to K-hop message passing by aggregating information from K-hop neighbors of nodes simultaneously. However, there is no work on analyzing the expressive power of K-hop message passing. In this work, we theoretically characterize the expressive power of K-hop message passing. Specifically, we first formally differentiate two kinds of kernels of K-hop message passing which are often misused in previous works. We then characterize the expressive power of K-hop message passing by showing that it is more powerful than 1-hop message passing. Despite the higher expressive power, we show that K-hop message passing still cannot distinguish some simple regular graphs. To further enhance its expressive power, we introduce a KP-GNN framework, which improves K-hop message passing by leveraging the peripheral subgraph information in each hop. We prove that KP-GNN can distinguish almost all regular graphs including some distance regular graphs which could not be distinguished by previous distance encoding methods. Experimental results verify the expressive power and effectiveness of KP-GNN. KP-GNN achieves competitive results across all benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge