Distance-Restricted Folklore Weisfeiler-Leman GNNs with Provable Cycle Counting Power
Paper and Code
Sep 10, 2023
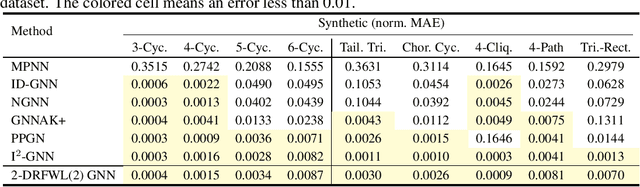
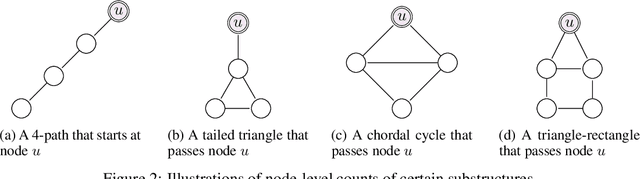
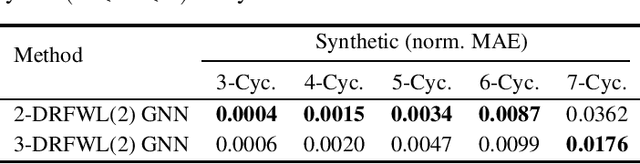
The ability of graph neural networks (GNNs) to count certain graph substructures, especially cycles, is important for the success of GNNs on a wide range of tasks. It has been recently used as a popular metric for evaluating the expressive power of GNNs. Many of the proposed GNN models with provable cycle counting power are based on subgraph GNNs, i.e., extracting a bag of subgraphs from the input graph, generating representations for each subgraph, and using them to augment the representation of the input graph. However, those methods require heavy preprocessing, and suffer from high time and memory costs. In this paper, we overcome the aforementioned limitations of subgraph GNNs by proposing a novel class of GNNs -- $d$-Distance-Restricted FWL(2) GNNs, or $d$-DRFWL(2) GNNs. $d$-DRFWL(2) GNNs use node pairs whose mutual distances are at most $d$ as the units for message passing to balance the expressive power and complexity. By performing message passing among distance-restricted node pairs in the original graph, $d$-DRFWL(2) GNNs avoid the expensive subgraph extraction operations in subgraph GNNs, making both the time and space complexity lower. We theoretically show that the discriminative power of $d$-DRFWL(2) GNNs strictly increases as $d$ increases. More importantly, $d$-DRFWL(2) GNNs have provably strong cycle counting power even with $d=2$: they can count all 3, 4, 5, 6-cycles. Since 6-cycles (e.g., benzene rings) are ubiquitous in organic molecules, being able to detect and count them is crucial for achieving robust and generalizable performance on molecular tasks. Experiments on both synthetic datasets and molecular datasets verify our theory. To the best of our knowledge, our model is the most efficient GNN model to date (both theoretically and empirically) that can count up to 6-cycles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge