Prompting Large Language Models for Clinical Temporal Relation Extraction

Objective: This paper aims to prompt large language models (LLMs) for clinical temporal relation extraction (CTRE) in both few-shot and fully supervised settings. Materials and Methods: This study utilizes four LLMs: Encoder-based GatorTron-Base (345M)/Large (8.9B); Decoder-based LLaMA3-8B/MeLLaMA-13B. We developed full (FFT) and parameter-efficient (PEFT) fine-tuning strategies and evaluated these strategies on the 2012 i2b2 CTRE task. We explored four fine-tuning strategies for GatorTron-Base: (1) Standard Fine-Tuning, (2) Hard-Prompting with Unfrozen LLMs, (3) Soft-Prompting with Frozen LLMs, and (4) Low-Rank Adaptation (LoRA) with Frozen LLMs. For GatorTron-Large, we assessed two PEFT strategies-Soft-Prompting and LoRA with Frozen LLMs-leveraging Quantization techniques. Additionally, LLaMA3-8B and MeLLaMA-13B employed two PEFT strategies: LoRA strategy with Quantization (QLoRA) applied to Frozen LLMs using instruction tuning and standard fine-tuning. Results: Under fully supervised settings, Hard-Prompting with Unfrozen GatorTron-Base achieved the highest F1 score (89.54%), surpassing the SOTA model (85.70%) by 3.74%. Additionally, two variants of QLoRA adapted to GatorTron-Large and Standard Fine-Tuning of GatorTron-Base exceeded the SOTA model by 2.36%, 1.88%, and 0.25%, respectively. Decoder-based models with frozen parameters outperformed their Encoder-based counterparts in this setting; however, the trend reversed in few-shot scenarios. Discussions and Conclusions: This study presented new methods that significantly improved CTRE performance, benefiting downstream tasks reliant on CTRE systems. The findings underscore the importance of selecting appropriate models and fine-tuning strategies based on task requirements and data availability. Future work will explore larger models and broader CTRE applications.

Practical Strategies of Active Learning to Rank for Web Search

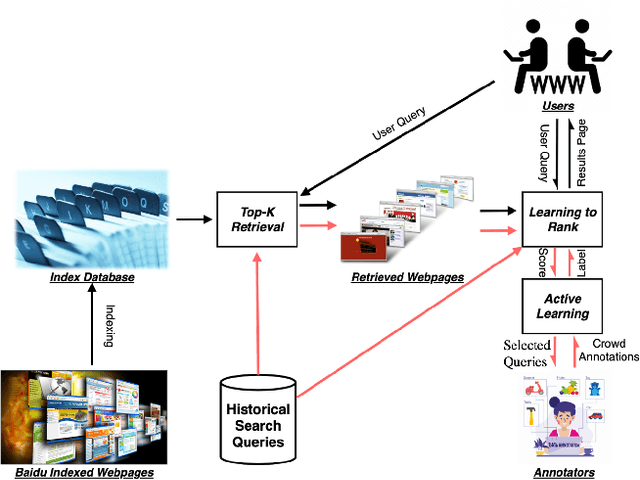
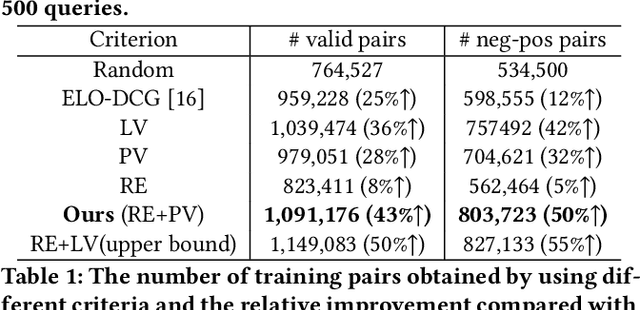
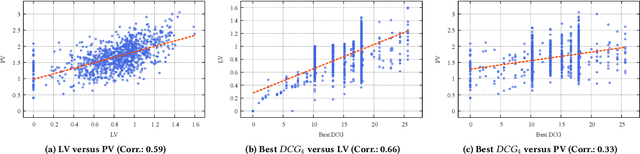
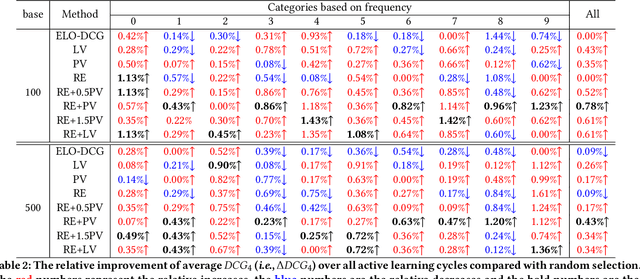
While China has become the biggest online market in the world with around 1 billion internet users, Baidu runs the world largest Chinese search engine serving more than hundreds of millions of daily active users and responding billions queries per day. To handle the diverse query requests from users at web-scale, Baidu has done tremendous efforts in understanding users' queries, retrieve relevant contents from a pool of trillions of webpages, and rank the most relevant webpages on the top of results. Among these components used in Baidu search, learning to rank (LTR) plays a critical role and we need to timely label an extremely large number of queries together with relevant webpages to train and update the online LTR models. To reduce the costs and time consumption of queries/webpages labeling, we study the problem of Activ Learning to Rank (active LTR) that selects unlabeled queries for annotation and training in this work. Specifically, we first investigate the criterion -- Ranking Entropy (RE) characterizing the entropy of relevant webpages under a query produced by a sequence of online LTR models updated by different checkpoints, using a Query-By-Committee (QBC) method. Then, we explore a new criterion namely Prediction Variances (PV) that measures the variance of prediction results for all relevant webpages under a query. Our empirical studies find that RE may favor low-frequency queries from the pool for labeling while PV prioritizing high-frequency queries more. Finally, we combine these two complementary criteria as the sample selection strategies for active learning. Extensive experiments with comparisons to baseline algorithms show that the proposed approach could train LTR models achieving higher Discounted Cumulative Gain (i.e., the relative improvement {\Delta}DCG4=1.38%) with the same budgeted labeling efforts.

Predicting COVID-19 Pneumonia Severity on Chest X-ray with Deep Learning

The need to streamline patient management for COVID-19 has become more pressing than ever. Chest X-rays provide a non-invasive (potentially bedside) tool to monitor the progression of the disease. In this study, we present a severity score prediction model for COVID-19 pneumonia for frontal chest X-ray images. Such a tool can gauge severity of COVID-19 lung infections (and pneumonia in general) that can be used for escalation or de-escalation of care as well as monitoring treatment efficacy, especially in the ICU. Images from a public COVID-19 database were scored retrospectively by three blinded experts in terms of the extent of lung involvement as well as the degree of opacity. A neural network model that was pre-trained on large (non-COVID-19) chest X-ray datasets is used to construct features for COVID-19 images which are predictive for our task. This study finds that training a regression model on a subset of the outputs from an this pre-trained chest X-ray model predicts our geographic extent score (range 0-8) with 1.14 mean absolute error (MAE) and our lung opacity score (range 0-6) with 0.78 MAE. All code, labels, and data are made available at https://github.com/mlmed/torchxrayvision and https://github.com/ieee8023/covid-chestxray-dataset

Finite Sample Analysis of LSTD with Random Projections and Eligibility Traces

Policy evaluation with linear function approximation is an important problem in reinforcement learning. When facing high-dimensional feature spaces, such a problem becomes extremely hard considering the computation efficiency and quality of approximations. We propose a new algorithm, LSTD($\lambda$)-RP, which leverages random projection techniques and takes eligibility traces into consideration to tackle the above two challenges. We carry out theoretical analysis of LSTD($\lambda$)-RP, and provide meaningful upper bounds of the estimation error, approximation error and total generalization error. These results demonstrate that LSTD($\lambda$)-RP can benefit from random projection and eligibility traces strategies, and LSTD($\lambda$)-RP can achieve better performances than prior LSTD-RP and LSTD($\lambda$) algorithms.

Thompson Sampling for Budgeted Multi-armed Bandits

Thompson sampling is one of the earliest randomized algorithms for multi-armed bandits (MAB). In this paper, we extend the Thompson sampling to Budgeted MAB, where there is random cost for pulling an arm and the total cost is constrained by a budget. We start with the case of Bernoulli bandits, in which the random rewards (costs) of an arm are independently sampled from a Bernoulli distribution. To implement the Thompson sampling algorithm in this case, at each round, we sample two numbers from the posterior distributions of the reward and cost for each arm, obtain their ratio, select the arm with the maximum ratio, and then update the posterior distributions. We prove that the distribution-dependent regret bound of this algorithm is $O(\ln B)$, where $B$ denotes the budget. By introducing a Bernoulli trial, we further extend this algorithm to the setting that the rewards (costs) are drawn from general distributions, and prove that its regret bound remains almost the same. Our simulation results demonstrate the effectiveness of the proposed algorithm.

Generalization Analysis for Game-Theoretic Machine Learning

For Internet applications like sponsored search, cautions need to be taken when using machine learning to optimize their mechanisms (e.g., auction) since self-interested agents in these applications may change their behaviors (and thus the data distribution) in response to the mechanisms. To tackle this problem, a framework called game-theoretic machine learning (GTML) was recently proposed, which first learns a Markov behavior model to characterize agents' behaviors, and then learns the optimal mechanism by simulating agents' behavior changes in response to the mechanism. While GTML has demonstrated practical success, its generalization analysis is challenging because the behavior data are non-i.i.d. and dependent on the mechanism. To address this challenge, first, we decompose the generalization error for GTML into the behavior learning error and the mechanism learning error; second, for the behavior learning error, we obtain novel non-asymptotic error bounds for both parametric and non-parametric behavior learning methods; third, for the mechanism learning error, we derive a uniform convergence bound based on a new concept called nested covering number of the mechanism space and the generalization analysis techniques developed for mixing sequences. To the best of our knowledge, this is the first work on the generalization analysis of GTML, and we believe it has general implications to the theoretical analysis of other complicated machine learning problems.

Agent Behavior Prediction and Its Generalization Analysis

Machine learning algorithms have been applied to predict agent behaviors in real-world dynamic systems, such as advertiser behaviors in sponsored search and worker behaviors in crowdsourcing. The behavior data in these systems are generated by live agents: once the systems change due to the adoption of the prediction models learnt from the behavior data, agents will observe and respond to these changes by changing their own behaviors accordingly. As a result, the behavior data will evolve and will not be identically and independently distributed, posing great challenges to the theoretical analysis on the machine learning algorithms for behavior prediction. To tackle this challenge, in this paper, we propose to use Markov Chain in Random Environments (MCRE) to describe the behavior data, and perform generalization analysis of the machine learning algorithms on its basis. Since the one-step transition probability matrix of MCRE depends on both previous states and the random environment, conventional techniques for generalization analysis cannot be directly applied. To address this issue, we propose a novel technique that transforms the original MCRE into a higher-dimensional time-homogeneous Markov chain. The new Markov chain involves more variables but is more regular, and thus easier to deal with. We prove the convergence of the new Markov chain when time approaches infinity. Then we prove a generalization bound for the machine learning algorithms on the behavior data generated by the new Markov chain, which depends on both the Markovian parameters and the covering number of the function class compounded by the loss function for behavior prediction and the behavior prediction model. To the best of our knowledge, this is the first work that performs the generalization analysis on data generated by complex processes in real-world dynamic systems.