BESTAnP: Bi-Step Efficient and Statistically Optimal Estimator for Acoustic-n-Point Problem

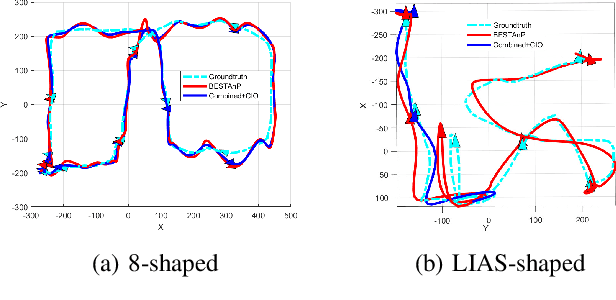
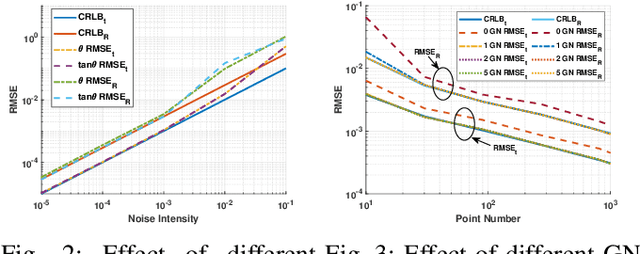
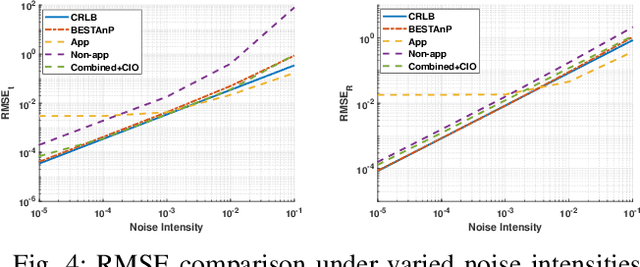
We consider the acoustic-n-point (AnP) problem, which estimates the pose of a 2D forward-looking sonar (FLS) according to n 3D-2D point correspondences. We explore the nature of the measured partial spherical coordinates and reveal their inherent relationships to translation and orientation. Based on this, we propose a bi-step efficient and statistically optimal AnP (BESTAnP) algorithm that decouples the estimation of translation and orientation. Specifically, in the first step, the translation estimation is formulated as the range-based localization problem based on distance-only measurements. In the second step, the rotation is estimated via eigendecomposition based on azimuth-only measurements and the estimated translation. BESTAnP is the first AnP algorithm that gives a closed-form solution for the full six-degree pose. In addition, we conduct bias elimination for BESTAnP such that it owns the statistical property of consistency. Through simulation and real-world experiments, we demonstrate that compared with the state-of-the-art (SOTA) methods, BESTAnP is over ten times faster and features real-time capacity in resource-constrained platforms while exhibiting comparable accuracy. Moreover, for the first time, we embed BESTAnP into a sonar-based odometry which shows its effectiveness for trajectory estimation.

Optimal camera-robot pose estimation in linear time from points and lines

Camera pose estimation is a fundamental problem in robotics. This paper focuses on two issues of interest: First, point and line features have complementary advantages, and it is of great value to design a uniform algorithm that can fuse them effectively; Second, with the development of modern front-end techniques, a large number of features can exist in a single image, which presents a potential for highly accurate robot pose estimation. With these observations, we propose AOPnP(L), an optimal linear-time camera-robot pose estimation algorithm from points and lines. Specifically, we represent a line with two distinct points on it and unify the noise model for point and line measurements where noises are added to 2D points in the image. By utilizing Plucker coordinates for line parameterization, we formulate a maximum likelihood (ML) problem for combined point and line measurements. To optimally solve the ML problem, AOPnP(L) adopts a two-step estimation scheme. In the first step, a consistent estimate that can converge to the true pose is devised by virtue of bias elimination. In the second step, a single Gauss-Newton iteration is executed to refine the initial estimate. AOPnP(L) features theoretical optimality in the sense that its mean squared error converges to the Cramer-Rao lower bound. Moreover, it owns a linear time complexity. These properties make it well-suited for precision-demanding and real-time robot pose estimation. Extensive experiments are conducted to validate our theoretical developments and demonstrate the superiority of AOPnP(L) in both static localization and dynamic odometry systems.

Fast Estimation of Relative Transformation Based on Fusion of Odometry and UWB Ranging Data

In this paper, we investigate the problem of estimating the 4-DOF (three-dimensional position and orientation) robot-robot relative frame transformation using odometers and distance measurements between robots. Firstly, we apply a two-step estimation method based on maximum likelihood estimation. Specifically, a good initial value is obtained through unconstrained least squares and projection, followed by a more accurate estimate achieved through one-step Gauss-Newton iteration. Additionally, the optimal installation positions of Ultra-Wideband (UWB) are provided, and the minimum operating time under different quantities of UWB devices is determined. Simulation demonstrates that the two-step approach offers faster computation with guaranteed accuracy while effectively addressing the relative transformation estimation problem within limited space constraints. Furthermore, this method can be applied to real-time relative transformation estimation when a specific number of UWB devices are installed.

Consistent and Asymptotically Statistically-Efficient Solution to Camera Motion Estimation

Given 2D point correspondences between an image pair, inferring the camera motion is a fundamental issue in the computer vision community. The existing works generally set out from the epipolar constraint and estimate the essential matrix, which is not optimal in the maximum likelihood (ML) sense. In this paper, we dive into the original measurement model with respect to the rotation matrix and normalized translation vector and formulate the ML problem. We then propose a two-step algorithm to solve it: In the first step, we estimate the variance of measurement noises and devise a consistent estimator based on bias elimination; In the second step, we execute a one-step Gauss-Newton iteration on manifold to refine the consistent estimate. We prove that the proposed estimate owns the same asymptotic statistical properties as the ML estimate: The first is consistency, i.e., the estimate converges to the ground truth as the point number increases; The second is asymptotic efficiency, i.e., the mean squared error of the estimate converges to the theoretical lower bound -- Cramer-Rao bound. In addition, we show that our algorithm has linear time complexity. These appealing characteristics endow our estimator with a great advantage in the case of dense point correspondences. Experiments on both synthetic data and real images demonstrate that when the point number reaches the order of hundreds, our estimator outperforms the state-of-the-art ones in terms of estimation accuracy and CPU time.

Efficient Invariant Kalman Filter for Inertial-based Odometry with Large-sample Environmental Measurements

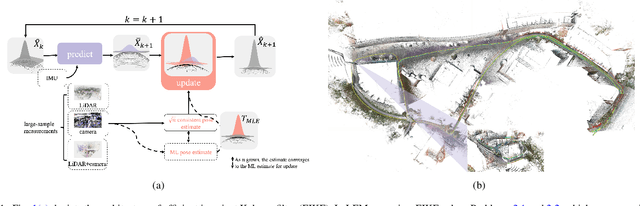
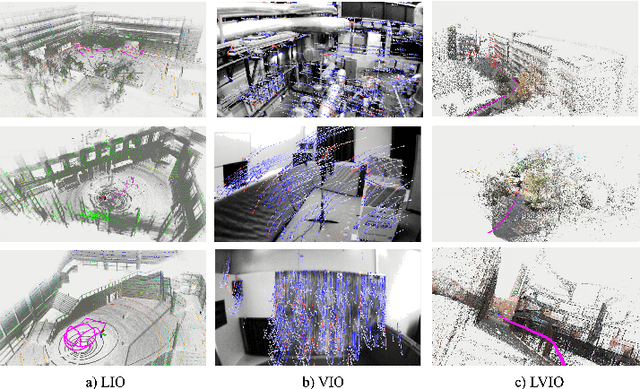
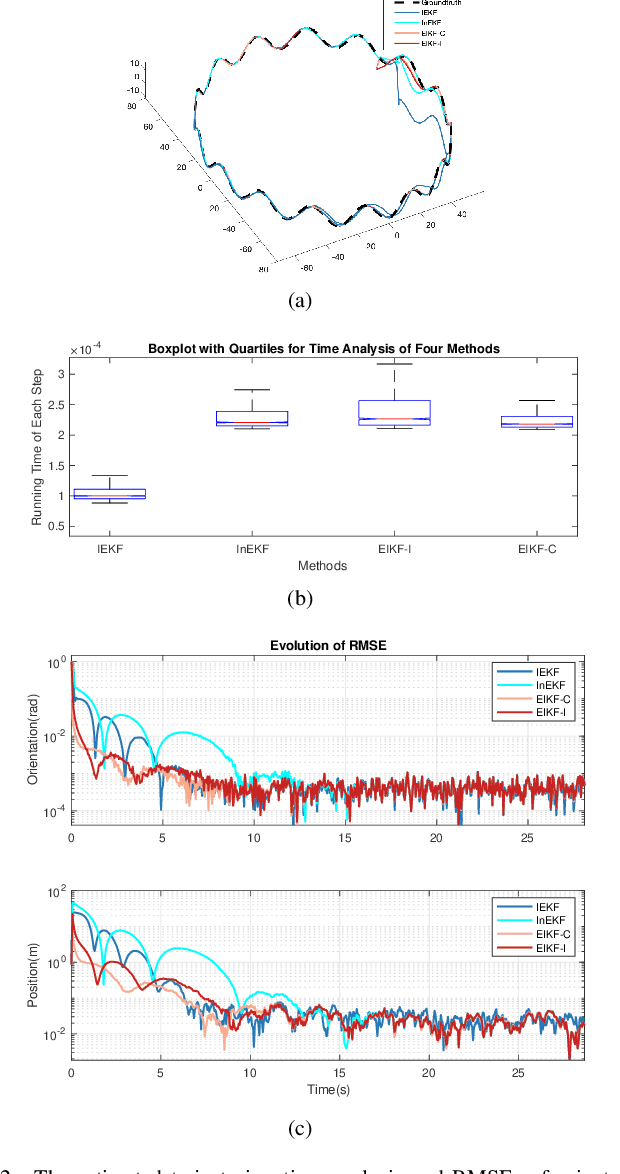
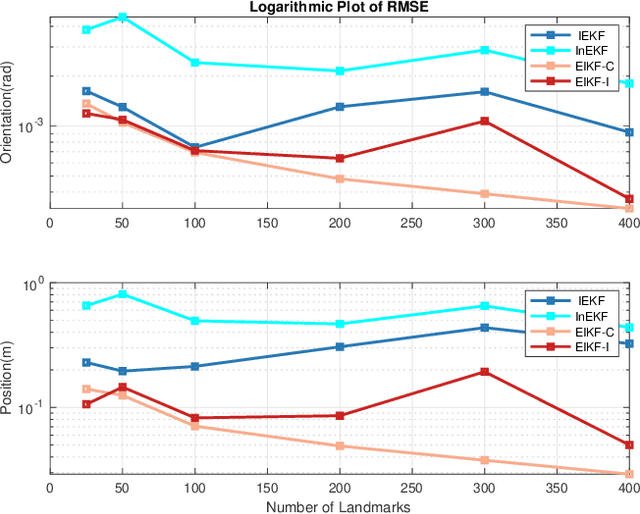
A filter for inertial-based odometry is a recursive method used to estimate the pose from measurements of ego-motion and relative pose. Currently, there is no known filter that guarantees the computation of a globally optimal solution for the non-linear measurement model. In this paper, we demonstrate that an innovative filter, with the state being $SE_2(3)$ and the $\sqrt{n}$-\textit{consistent} pose as the initialization, efficiently achieves \textit{asymptotic optimality} in terms of minimum mean square error. This approach is tailored for real-time SLAM and inertial-based odometry applications. Our first contribution is that we propose an iterative filtering method based on the Gauss-Newton method on Lie groups which is numerically to solve the estimation of states from a priori and non-linear measurements. The filtering stands out due to its iterative mechanism and adaptive initialization. Second, when dealing with environmental measurements of the surroundings, we utilize a $\sqrt{n}$-consistent pose as the initial value for the update step in a single iteration. The solution is closed in form and has computational complexity $O(n)$. Third, we theoretically show that the approach can achieve asymptotic optimality in the sense of minimum mean square error from the a priori and virtual relative pose measurements (see Problem~\ref{prob:new update problem}). Finally, to validate our method, we carry out extensive numerical and experimental evaluations. Our results consistently demonstrate that our approach outperforms other state-of-the-art filter-based methods, including the iterated extended Kalman filter and the invariant extended Kalman filter, in terms of accuracy and running time.

Consistent and Asymptotically Efficient Localization from Range-Difference Measurements

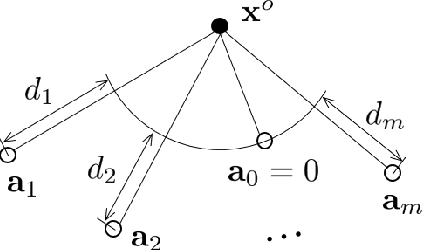
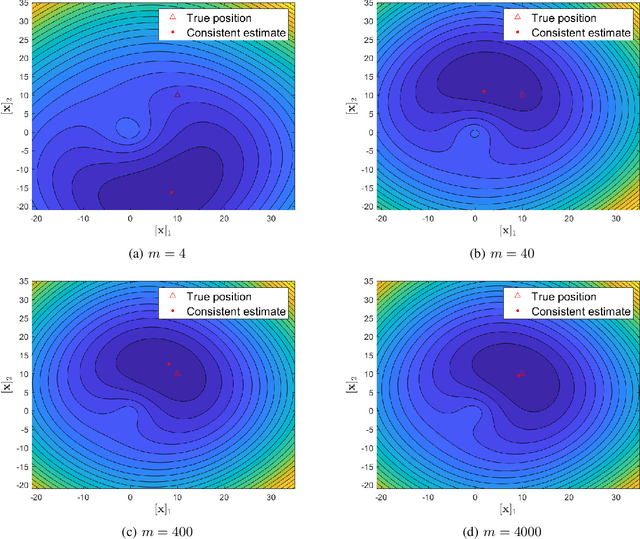
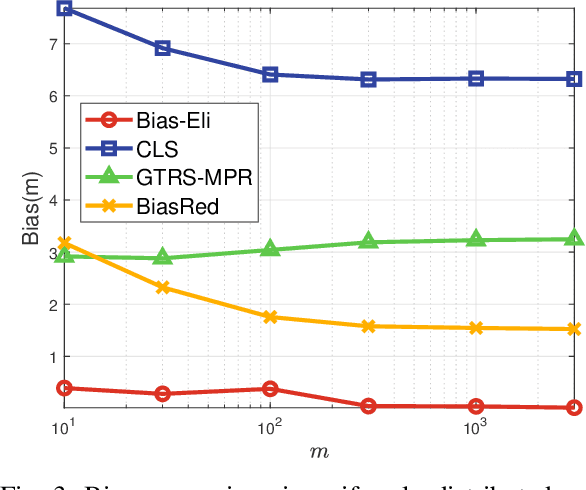
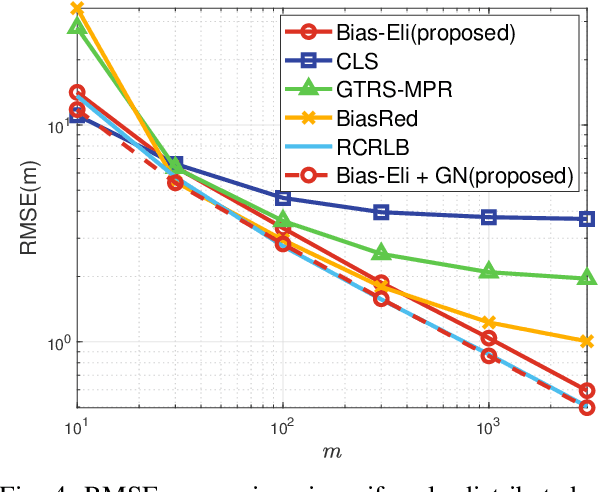
We consider signal source localization from range-difference measurements. First, we give some readily-checked conditions on measurement noises and sensor deployment to guarantee the asymptotic identifiability of the model and show the consistency and asymptotic normality of the maximum likelihood (ML) estimator. Then, we devise an estimator that owns the same asymptotic property as the ML one. Specifically, we prove that the negative log-likelihood function converges to a function, which has a unique minimum and positive-definite Hessian at the true source's position. Hence, it is promising to execute local iterations, e.g., the Gauss-Newton (GN) algorithm, following a consistent estimate. The main issue involved is obtaining a preliminary consistent estimate. To this aim, we construct a linear least-squares problem via algebraic operation and constraint relaxation and obtain a closed-form solution. We then focus on deriving and eliminating the bias of the linear least-squares estimator, which yields an asymptotically unbiased (thus consistent) estimate. Noting that the bias is a function of the noise variance, we further devise a consistent noise variance estimator which involves $3$-order polynomial rooting. Based on the preliminary consistent location estimate, we prove that a one-step GN iteration suffices to achieve the same asymptotic property as the ML estimator. Simulation results demonstrate the superiority of our proposed algorithm in the large sample case.

CPnP: Consistent Pose Estimator for Perspective-n-Point Problem with Bias Elimination

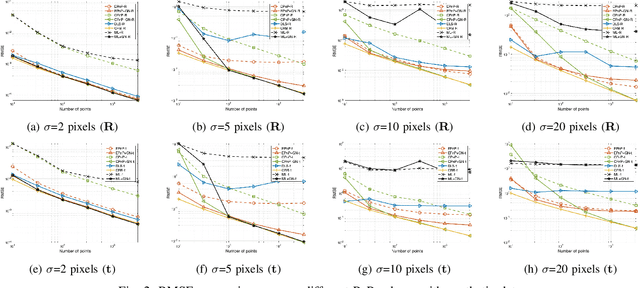
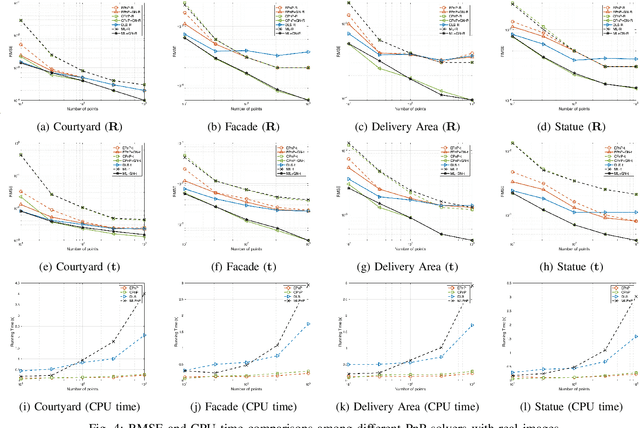
The Perspective-n-Point (PnP) problem has been widely studied in both computer vision and photogrammetry societies. With the development of feature extraction techniques, a large number of feature points might be available in a single shot. It is promising to devise a consistent estimator, i.e., the estimate can converge to the true camera pose as the number of points increases. To this end, we propose a consistent PnP solver, named \emph{CPnP}, with bias elimination. Specifically, linear equations are constructed from the original projection model via measurement model modification and variable elimination, based on which a closed-form least-squares solution is obtained. We then analyze and subtract the asymptotic bias of this solution, resulting in a consistent estimate. Additionally, Gauss-Newton (GN) iterations are executed to refine the consistent solution. Our proposed estimator is efficient in terms of computations -- it has $O(n)$ computational complexity. Experimental tests on both synthetic data and real images show that our proposed estimator is superior to some well-known ones for images with dense visual features, in terms of estimation precision and computing time.

Global and Asymptotically Efficient Localization from Range Measurements

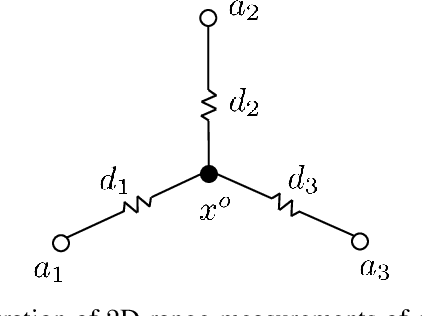
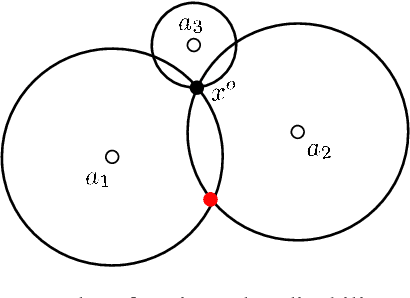
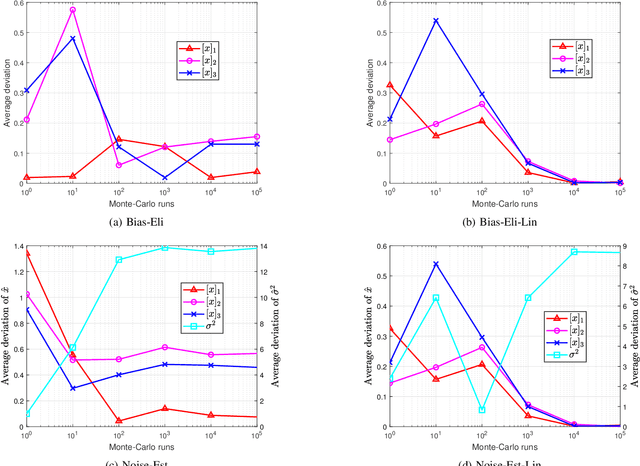
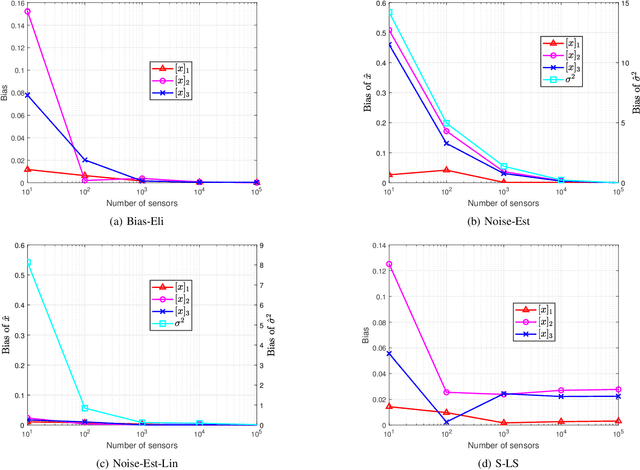
We consider the range-based localization problem, which involves estimating an object's position by using $m$ sensors, hoping that as the number $m$ of sensors increases, the estimate converges to the true position with the minimum variance. We show that under some conditions on the sensor deployment and measurement noises, the LS estimator is strongly consistent and asymptotically normal. However, the LS problem is nonsmooth and nonconvex, and therefore hard to solve. We then devise realizable estimators that possess the same asymptotic properties as the LS one. These estimators are based on a two-step estimation architecture, which says that any $\sqrt{m}$-consistent estimate followed by a one-step Gauss-Newton iteration can yield a solution that possesses the same asymptotic property as the LS one. The keypoint of the two-step scheme is to construct a $\sqrt{m}$-consistent estimate in the first step. In terms of whether the variance of measurement noises is known or not, we propose the Bias-Eli estimator (which involves solving a generalized trust region subproblem) and the Noise-Est estimator (which is obtained by solving a convex problem), respectively. Both of them are proved to be $\sqrt{m}$-consistent. Moreover, we show that by discarding the constraints in the above two optimization problems, the resulting closed-form estimators (called Bias-Eli-Lin and Noise-Est-Lin) are also $\sqrt{m}$-consistent. Plenty of simulations verify the correctness of our theoretical claims, showing that the proposed two-step estimators can asymptotically achieve the Cramer-Rao lower bound.

Low-complexity Distributed Detection with One-bit Memory Under Neyman-Pearson Criterion

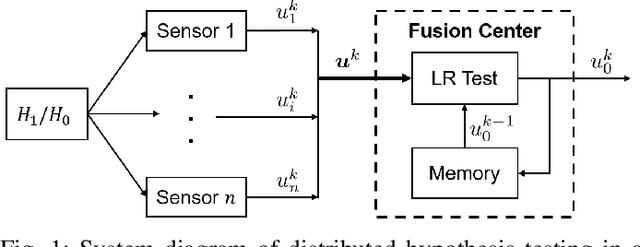
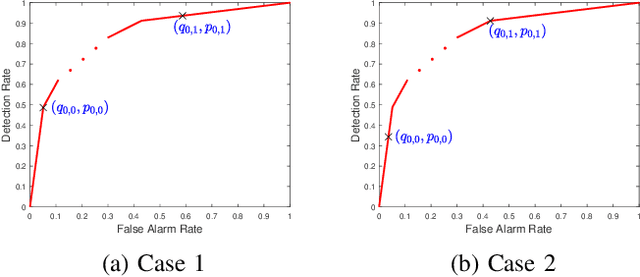
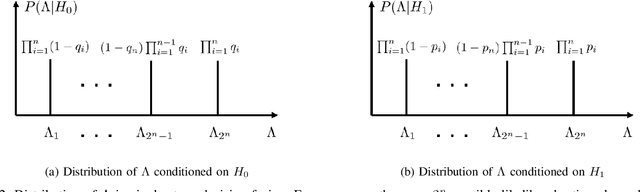
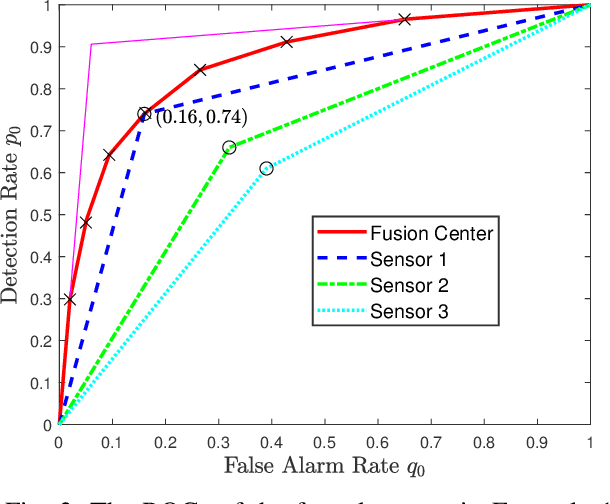
We consider a multi-stage distributed detection scenario, where $n$ sensors and a fusion center (FC) are deployed to accomplish a binary hypothesis test. At each time stage, local sensors generate binary messages, assumed to be spatially and temporally independent given the hypothesis, and then upload them to the FC for global detection decision making. We suppose a one-bit memory is available at the FC to store its decision history and focus on developing iterative fusion schemes. We first visit the detection problem of performing the Neyman-Pearson (N-P) test at each stage and give an optimal algorithm, called the oracle algorithm, to solve it. Structural properties and limitation of the fusion performance in the asymptotic regime are explored for the oracle algorithm. We notice the computational inefficiency of the oracle fusion and propose a low-complexity alternative, for which the likelihood ratio (LR) test threshold is tuned in connection to the fusion decision history compressed in the one-bit memory. The low-complexity algorithm greatly brings down the computational complexity at each stage from $O(4^n)$ to $O(n)$. We show that the proposed algorithm is capable of converging exponentially to the same detection probability as that of the oracle one. Moreover, the rate of convergence is shown to be asymptotically identical to that of the oracle algorithm. Finally, numerical simulations and real-world experiments demonstrate the effectiveness and efficiency of our distributed algorithm.