Consistent and Asymptotically Efficient Localization from Range-Difference Measurements
Paper and Code
Feb 10, 2023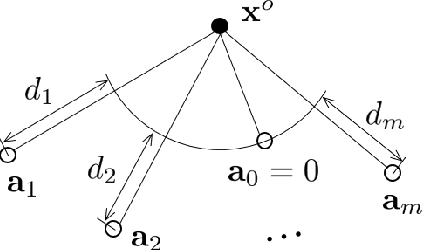
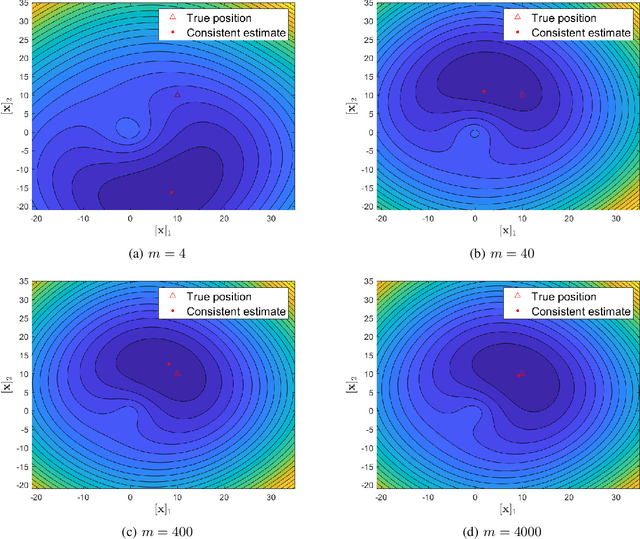
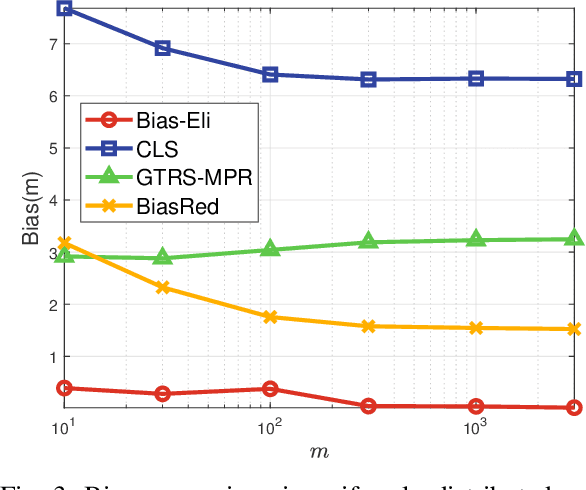
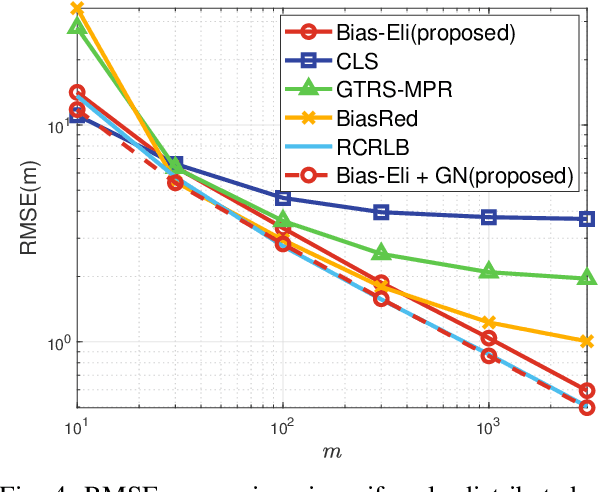
We consider signal source localization from range-difference measurements. First, we give some readily-checked conditions on measurement noises and sensor deployment to guarantee the asymptotic identifiability of the model and show the consistency and asymptotic normality of the maximum likelihood (ML) estimator. Then, we devise an estimator that owns the same asymptotic property as the ML one. Specifically, we prove that the negative log-likelihood function converges to a function, which has a unique minimum and positive-definite Hessian at the true source's position. Hence, it is promising to execute local iterations, e.g., the Gauss-Newton (GN) algorithm, following a consistent estimate. The main issue involved is obtaining a preliminary consistent estimate. To this aim, we construct a linear least-squares problem via algebraic operation and constraint relaxation and obtain a closed-form solution. We then focus on deriving and eliminating the bias of the linear least-squares estimator, which yields an asymptotically unbiased (thus consistent) estimate. Noting that the bias is a function of the noise variance, we further devise a consistent noise variance estimator which involves $3$-order polynomial rooting. Based on the preliminary consistent location estimate, we prove that a one-step GN iteration suffices to achieve the same asymptotic property as the ML estimator. Simulation results demonstrate the superiority of our proposed algorithm in the large sample case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge