Consistent and Asymptotically Statistically-Efficient Solution to Camera Motion Estimation

Given 2D point correspondences between an image pair, inferring the camera motion is a fundamental issue in the computer vision community. The existing works generally set out from the epipolar constraint and estimate the essential matrix, which is not optimal in the maximum likelihood (ML) sense. In this paper, we dive into the original measurement model with respect to the rotation matrix and normalized translation vector and formulate the ML problem. We then propose a two-step algorithm to solve it: In the first step, we estimate the variance of measurement noises and devise a consistent estimator based on bias elimination; In the second step, we execute a one-step Gauss-Newton iteration on manifold to refine the consistent estimate. We prove that the proposed estimate owns the same asymptotic statistical properties as the ML estimate: The first is consistency, i.e., the estimate converges to the ground truth as the point number increases; The second is asymptotic efficiency, i.e., the mean squared error of the estimate converges to the theoretical lower bound -- Cramer-Rao bound. In addition, we show that our algorithm has linear time complexity. These appealing characteristics endow our estimator with a great advantage in the case of dense point correspondences. Experiments on both synthetic data and real images demonstrate that when the point number reaches the order of hundreds, our estimator outperforms the state-of-the-art ones in terms of estimation accuracy and CPU time.

Efficient Invariant Kalman Filter for Inertial-based Odometry with Large-sample Environmental Measurements

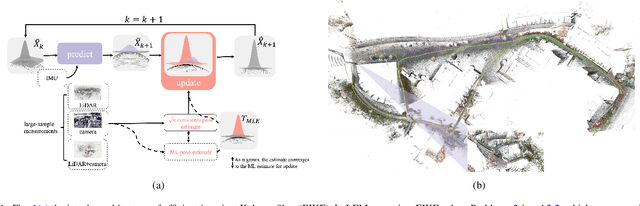
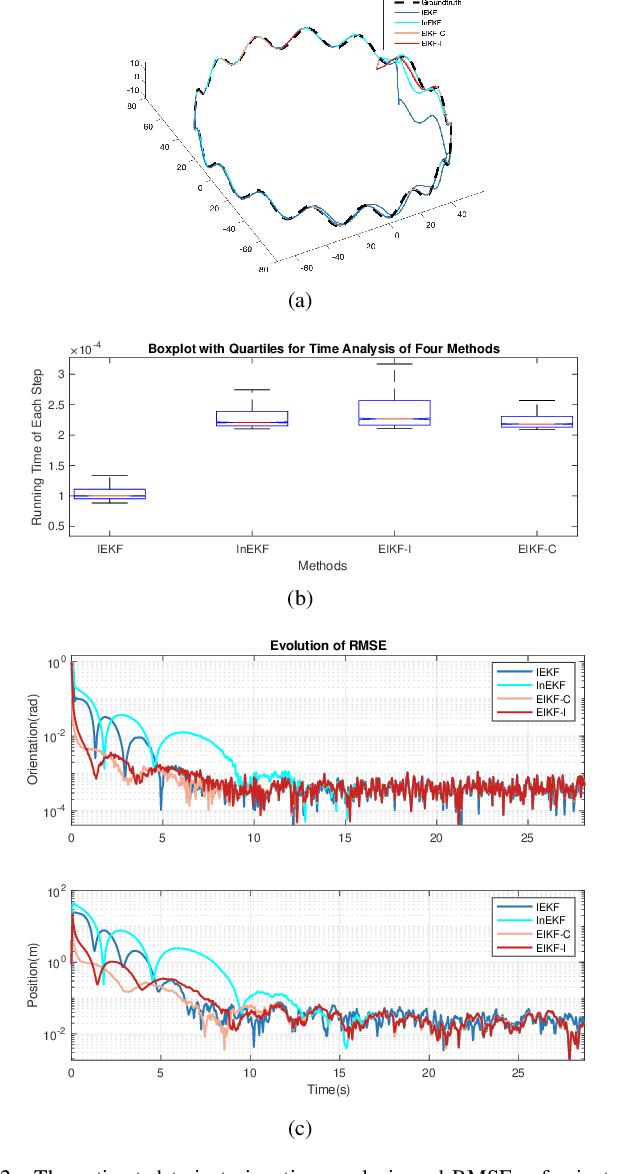
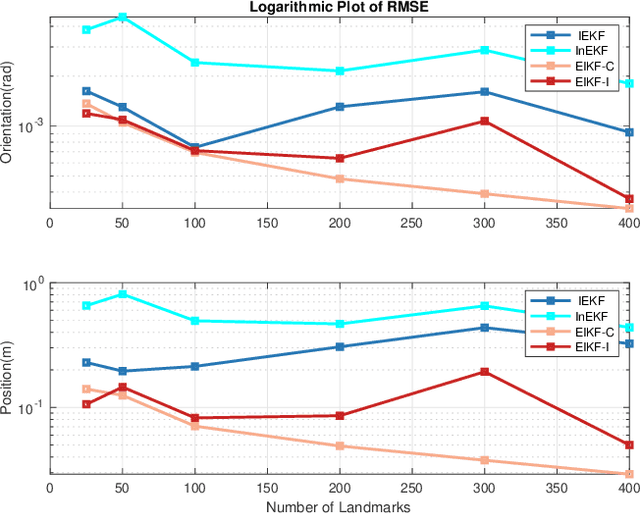
A filter for inertial-based odometry is a recursive method used to estimate the pose from measurements of ego-motion and relative pose. Currently, there is no known filter that guarantees the computation of a globally optimal solution for the non-linear measurement model. In this paper, we demonstrate that an innovative filter, with the state being $SE_2(3)$ and the $\sqrt{n}$-\textit{consistent} pose as the initialization, efficiently achieves \textit{asymptotic optimality} in terms of minimum mean square error. This approach is tailored for real-time SLAM and inertial-based odometry applications. Our first contribution is that we propose an iterative filtering method based on the Gauss-Newton method on Lie groups which is numerically to solve the estimation of states from a priori and non-linear measurements. The filtering stands out due to its iterative mechanism and adaptive initialization. Second, when dealing with environmental measurements of the surroundings, we utilize a $\sqrt{n}$-consistent pose as the initial value for the update step in a single iteration. The solution is closed in form and has computational complexity $O(n)$. Third, we theoretically show that the approach can achieve asymptotic optimality in the sense of minimum mean square error from the a priori and virtual relative pose measurements (see Problem~\ref{prob:new update problem}). Finally, to validate our method, we carry out extensive numerical and experimental evaluations. Our results consistently demonstrate that our approach outperforms other state-of-the-art filter-based methods, including the iterated extended Kalman filter and the invariant extended Kalman filter, in terms of accuracy and running time.

Efficient Planar Pose Estimation via UWB Measurements

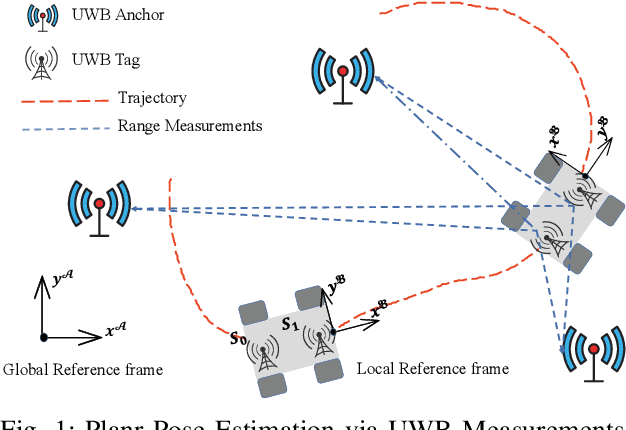
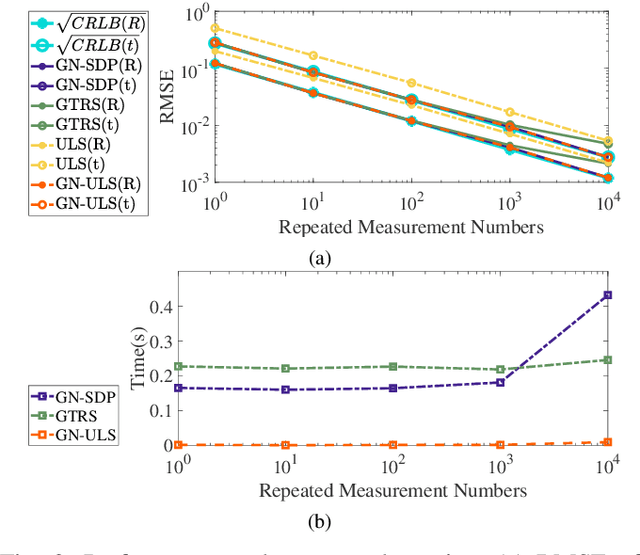
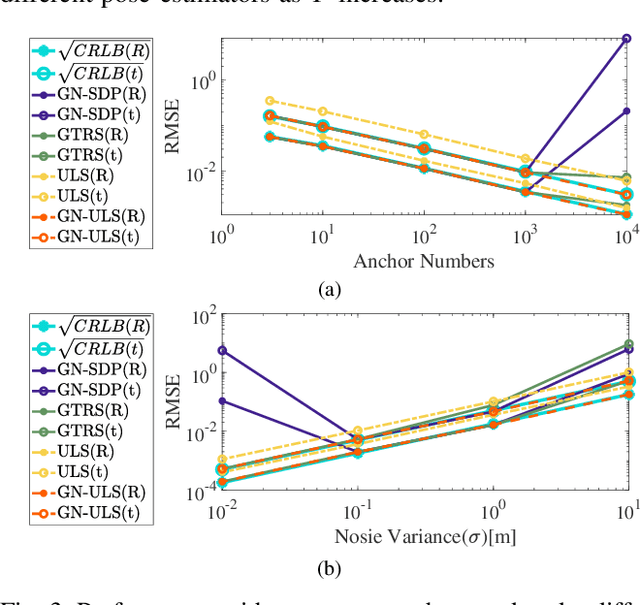
State estimation is an essential part of autonomous systems. Integrating the Ultra-Wideband(UWB) technique has been shown to correct the long-term estimation drift and bypass the complexity of loop closure detection. However, few works on robotics adopt UWB as a stand-alone state estimation solution. The primary purpose of this work is to investigate planar pose estimation using only UWB range measurements and study the estimator's statistical efficiency. We prove the excellent property of a two-step scheme, which says that we can refine a consistent estimator to be asymptotically efficient by one step of Gauss-Newton iteration. Grounded on this result, we design the GN-ULS estimator and evaluate it through simulations and collected datasets. GN-ULS attains millimeter and sub-degree level accuracy on our static datasets and attains centimeter and degree level accuracy on our dynamic datasets, presenting the possibility of using only UWB for real-time state estimation.

Closed-form Error Propagation on the SE_n Group for Invariant Extended Kalman Filtering with Applications to VINS

Pose estimation is important for robotic perception, path planning, etc. Robot poses can be modeled on matrix Lie groups and are usually estimated via filter-based methods. In this paper, we establish the closed-form formula for the error propagation for the Invariant extended Kalman filter (IEKF) in the presence of random noises and apply it to vision-aided inertial navigation. We evaluate our algorithm via numerical simulations and experiments on the OPENVINS platform. Both simulations and the experiments performed on the public EuRoC MAV datasets demonstrate that our algorithm outperforms some state-of-art filter-based methods such as the quaternion-based EKF, first estimates Jacobian EKF, etc.