Optimal camera-robot pose estimation in linear time from points and lines

Camera pose estimation is a fundamental problem in robotics. This paper focuses on two issues of interest: First, point and line features have complementary advantages, and it is of great value to design a uniform algorithm that can fuse them effectively; Second, with the development of modern front-end techniques, a large number of features can exist in a single image, which presents a potential for highly accurate robot pose estimation. With these observations, we propose AOPnP(L), an optimal linear-time camera-robot pose estimation algorithm from points and lines. Specifically, we represent a line with two distinct points on it and unify the noise model for point and line measurements where noises are added to 2D points in the image. By utilizing Plucker coordinates for line parameterization, we formulate a maximum likelihood (ML) problem for combined point and line measurements. To optimally solve the ML problem, AOPnP(L) adopts a two-step estimation scheme. In the first step, a consistent estimate that can converge to the true pose is devised by virtue of bias elimination. In the second step, a single Gauss-Newton iteration is executed to refine the initial estimate. AOPnP(L) features theoretical optimality in the sense that its mean squared error converges to the Cramer-Rao lower bound. Moreover, it owns a linear time complexity. These properties make it well-suited for precision-demanding and real-time robot pose estimation. Extensive experiments are conducted to validate our theoretical developments and demonstrate the superiority of AOPnP(L) in both static localization and dynamic odometry systems.

CPnP: Consistent Pose Estimator for Perspective-n-Point Problem with Bias Elimination

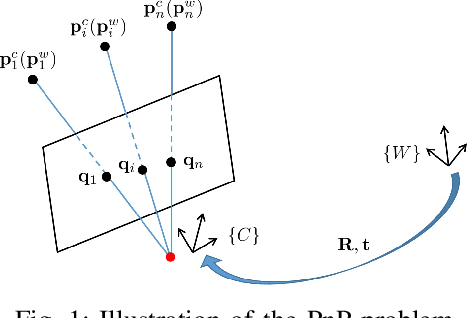
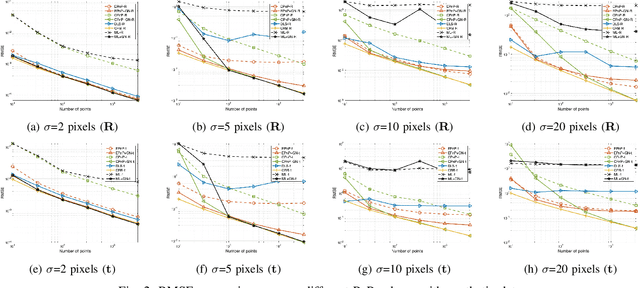
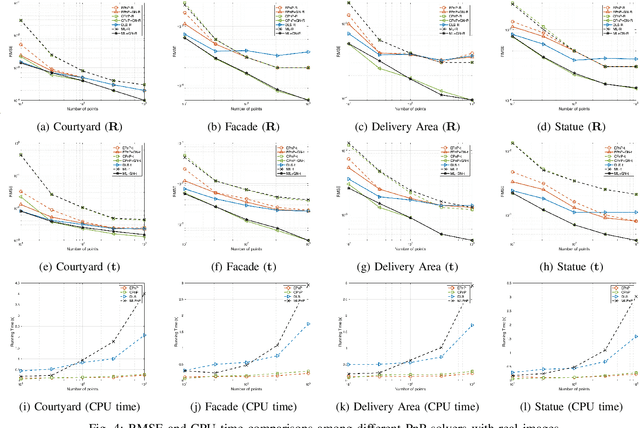
The Perspective-n-Point (PnP) problem has been widely studied in both computer vision and photogrammetry societies. With the development of feature extraction techniques, a large number of feature points might be available in a single shot. It is promising to devise a consistent estimator, i.e., the estimate can converge to the true camera pose as the number of points increases. To this end, we propose a consistent PnP solver, named \emph{CPnP}, with bias elimination. Specifically, linear equations are constructed from the original projection model via measurement model modification and variable elimination, based on which a closed-form least-squares solution is obtained. We then analyze and subtract the asymptotic bias of this solution, resulting in a consistent estimate. Additionally, Gauss-Newton (GN) iterations are executed to refine the consistent solution. Our proposed estimator is efficient in terms of computations -- it has $O(n)$ computational complexity. Experimental tests on both synthetic data and real images show that our proposed estimator is superior to some well-known ones for images with dense visual features, in terms of estimation precision and computing time.

Learning Stable Koopman Embeddings

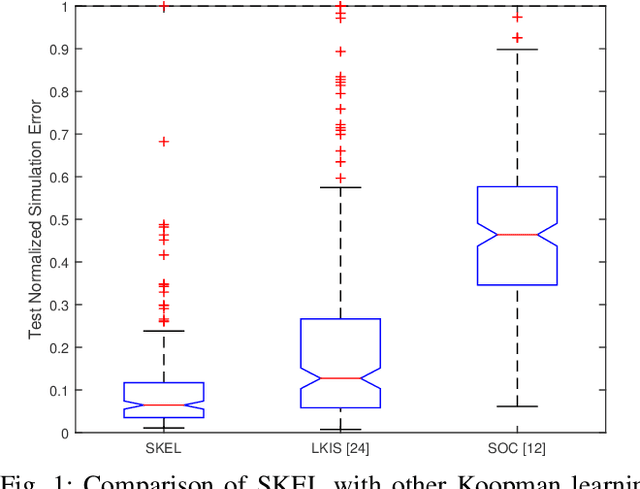
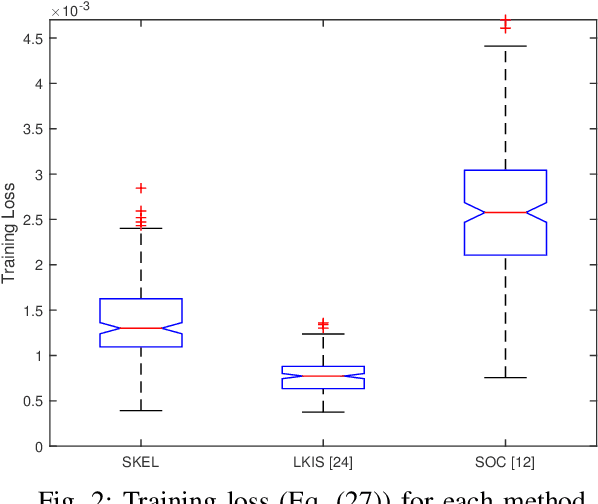
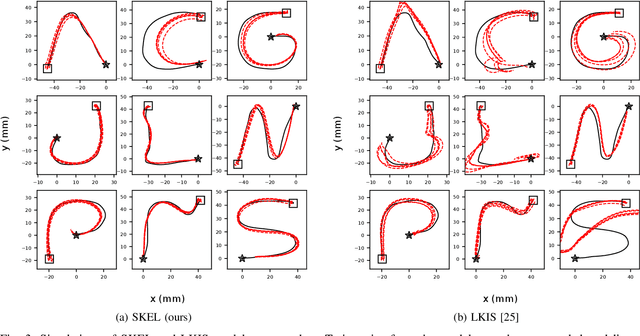
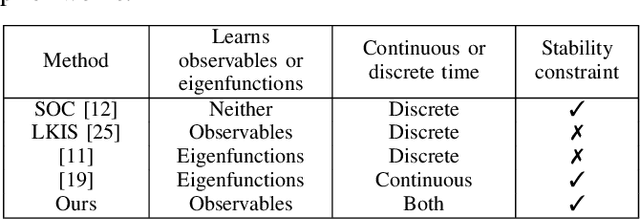
In this paper, we present a new data-driven method for learning stable models of nonlinear systems. Our model lifts the original state space to a higher-dimensional linear manifold using Koopman embeddings. Interestingly, we prove that every discrete-time nonlinear contracting model can be learnt in our framework. Another significant merit of the proposed approach is that it allows for unconstrained optimization over the Koopman embedding and operator jointly while enforcing stability of the model, via a direct parameterization of stable linear systems, greatly simplifying the computations involved. We validate our method on a simulated system and analyze the advantages of our parameterization compared to alternatives.

Fast-Learning Grasping and Pre-Grasping via Clutter Quantization and Q-map Masking

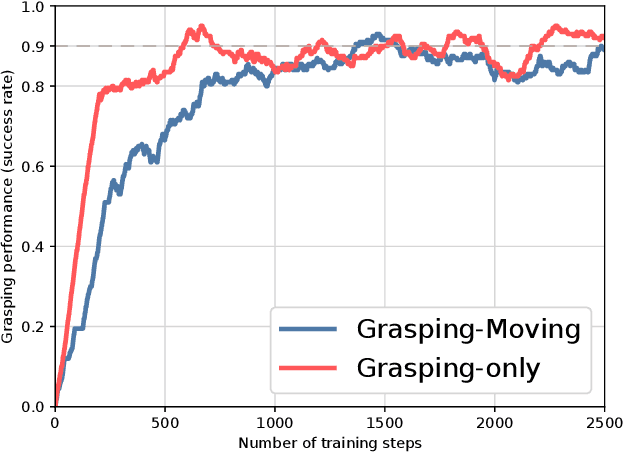
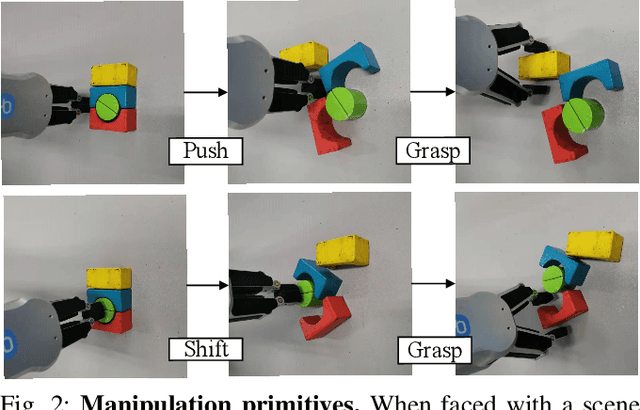
Grasping objects in cluttered scenarios is a challenging task in robotics. Performing pre-grasp actions such as pushing and shifting to scatter objects is a way to reduce clutter. Based on deep reinforcement learning, we propose a Fast-Learning Grasping (FLG) framework, that can integrate pre-grasping actions along with grasping to pick up objects from cluttered scenarios with reduced real-world training time. We associate rewards for performing moving actions with the change of environmental clutter and utilize a hybrid triggering method, leading to data-efficient learning and synergy. Then we use the output of an extended fully convolutional network as the value function of each pixel point of the workspace and establish an accurate estimation of the grasp probability for each action. We also introduce a mask function as prior knowledge to enable the agents to focus on the accurate pose adjustment to improve the effectiveness of collecting training data and, hence, to learn efficiently. We carry out pre-training of the FLG over simulated environment, and then the learnt model is transferred to the real world with minimal fine-tuning for further learning during actions. Experimental results demonstrate a 94% grasp success rate and the ability to generalize to novel objects. Compared to state-of-the-art approaches in the literature, the proposed FLG framework can achieve similar or higher grasp success rate with lesser amount of training in the real world. Supplementary video is available at https://youtu.be/e04uDLsxfDg.

An almost globally convergent observer for visual SLAM without persistent excitation

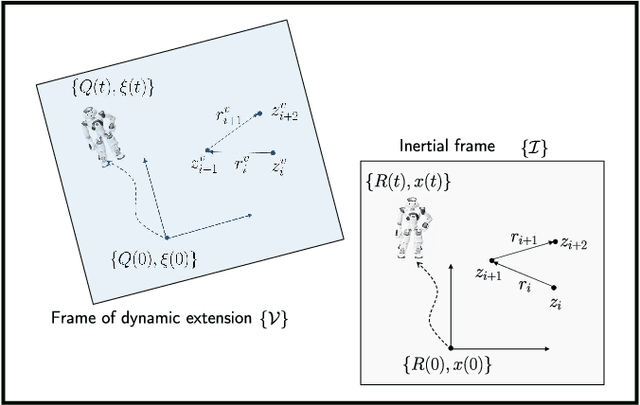
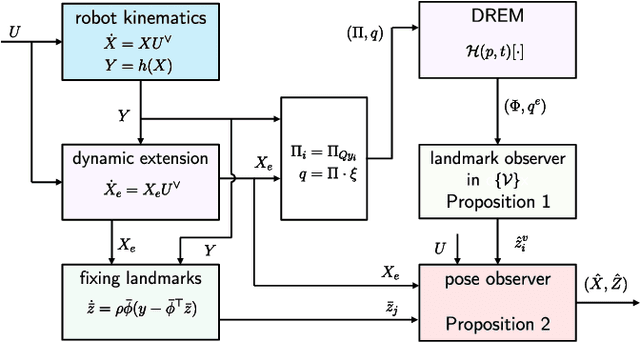
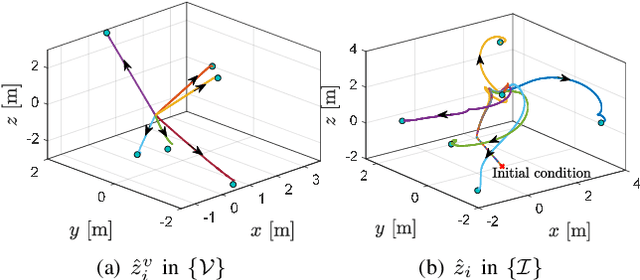
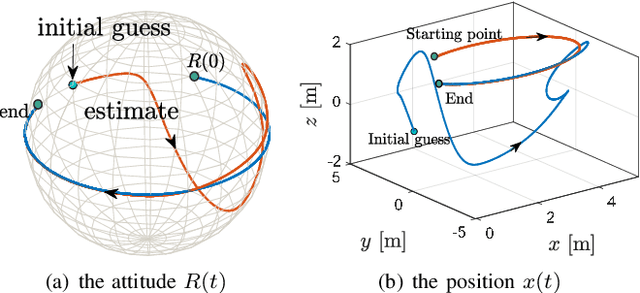
In this paper we propose a novel observer to solve the problem of visual simultaneous localization and mapping, using the information of only the bearing vectors of landmarks observed from a single monocular camera and body-fixed velocities. The system state evolves on the manifold $SE(3)\times \mathbb{R}^{3n}$, on which we design dynamic extensions carefully in order to generate an invariant foliation, such that the problem is reformulated into online parameter identification. Then, following the recently introduced parameter estimation-based observer, we provide a novel and simple solution to address the problem. A notable merit is that the proposed observer guarantees almost global asymptotic stability requiring neither persistent excitation nor uniform complete observability, which, however, are widely adopted in the existing works.

Distributed Online Optimization with Long-Term Constraints

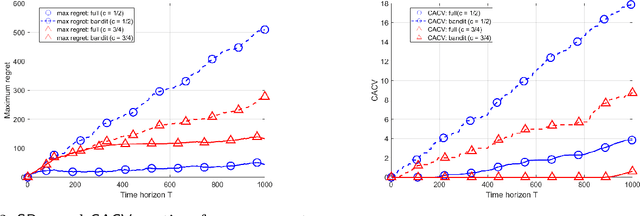
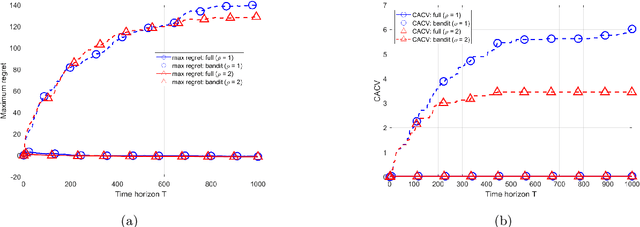
We consider distributed online convex optimization problems, where the distributed system consists of various computing units connected through a time-varying communication graph. In each time step, each computing unit selects a constrained vector, experiences a loss equal to an arbitrary convex function evaluated at this vector, and may communicate to its neighbors in the graph. The objective is to minimize the system-wide loss accumulated over time. We propose a decentralized algorithm with regret and cumulative constraint violation in $\mathcal{O}(T^{\max\{c,1-c\} })$ and $\mathcal{O}(T^{1-c/2})$, respectively, for any $c\in (0,1)$, where $T$ is the time horizon. When the loss functions are strongly convex, we establish improved regret and constraint violation upper bounds in $\mathcal{O}(\log(T))$ and $\mathcal{O}(\sqrt{T\log(T)})$. These regret scalings match those obtained by state-of-the-art algorithms and fundamental limits in the corresponding centralized online optimization problem (for both convex and strongly convex loss functions). In the case of bandit feedback, the proposed algorithms achieve a regret and constraint violation in $\mathcal{O}(T^{\max\{c,1-c/3 \} })$ and $\mathcal{O}(T^{1-c/2})$ for any $c\in (0,1)$. We numerically illustrate the performance of our algorithms for the particular case of distributed online regularized linear regression problems.

Distributed Online Linear Regression

We study online linear regression problems in a distributed setting, where the data is spread over a network. In each round, each network node proposes a linear predictor, with the objective of fitting the \emph{network-wide} data. It then updates its predictor for the next round according to the received local feedback and information received from neighboring nodes. The predictions made at a given node are assessed through the notion of regret, defined as the difference between their cumulative network-wide square errors and those of the best off-line network-wide linear predictor. Various scenarios are investigated, depending on the nature of the local feedback (full information or bandit feedback), on the set of available predictors (the decision set), and the way data is generated (by an oblivious or adaptive adversary). We propose simple and natural distributed regression algorithms, involving, at each node and in each round, a local gradient descent step and a communication and averaging step where nodes aim at aligning their predictors to those of their neighbors. We establish regret upper bounds typically in ${\cal O}(T^{3/4})$ when the decision set is unbounded and in ${\cal O}(\sqrt{T})$ in case of bounded decision set.