Distributed Online Optimization with Long-Term Constraints

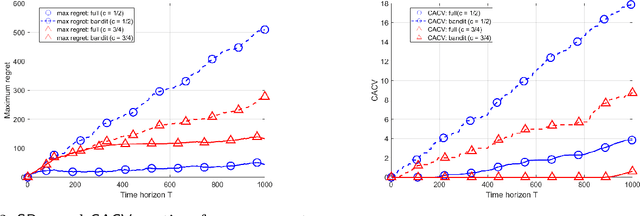
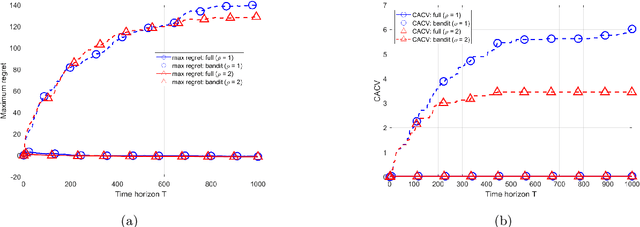
We consider distributed online convex optimization problems, where the distributed system consists of various computing units connected through a time-varying communication graph. In each time step, each computing unit selects a constrained vector, experiences a loss equal to an arbitrary convex function evaluated at this vector, and may communicate to its neighbors in the graph. The objective is to minimize the system-wide loss accumulated over time. We propose a decentralized algorithm with regret and cumulative constraint violation in $\mathcal{O}(T^{\max\{c,1-c\} })$ and $\mathcal{O}(T^{1-c/2})$, respectively, for any $c\in (0,1)$, where $T$ is the time horizon. When the loss functions are strongly convex, we establish improved regret and constraint violation upper bounds in $\mathcal{O}(\log(T))$ and $\mathcal{O}(\sqrt{T\log(T)})$. These regret scalings match those obtained by state-of-the-art algorithms and fundamental limits in the corresponding centralized online optimization problem (for both convex and strongly convex loss functions). In the case of bandit feedback, the proposed algorithms achieve a regret and constraint violation in $\mathcal{O}(T^{\max\{c,1-c/3 \} })$ and $\mathcal{O}(T^{1-c/2})$ for any $c\in (0,1)$. We numerically illustrate the performance of our algorithms for the particular case of distributed online regularized linear regression problems.

Distributed Online Linear Regression

We study online linear regression problems in a distributed setting, where the data is spread over a network. In each round, each network node proposes a linear predictor, with the objective of fitting the \emph{network-wide} data. It then updates its predictor for the next round according to the received local feedback and information received from neighboring nodes. The predictions made at a given node are assessed through the notion of regret, defined as the difference between their cumulative network-wide square errors and those of the best off-line network-wide linear predictor. Various scenarios are investigated, depending on the nature of the local feedback (full information or bandit feedback), on the set of available predictors (the decision set), and the way data is generated (by an oblivious or adaptive adversary). We propose simple and natural distributed regression algorithms, involving, at each node and in each round, a local gradient descent step and a communication and averaging step where nodes aim at aligning their predictors to those of their neighbors. We establish regret upper bounds typically in ${\cal O}(T^{3/4})$ when the decision set is unbounded and in ${\cal O}(\sqrt{T})$ in case of bounded decision set.