Learning Stable Koopman Embeddings
Paper and Code
Oct 13, 2021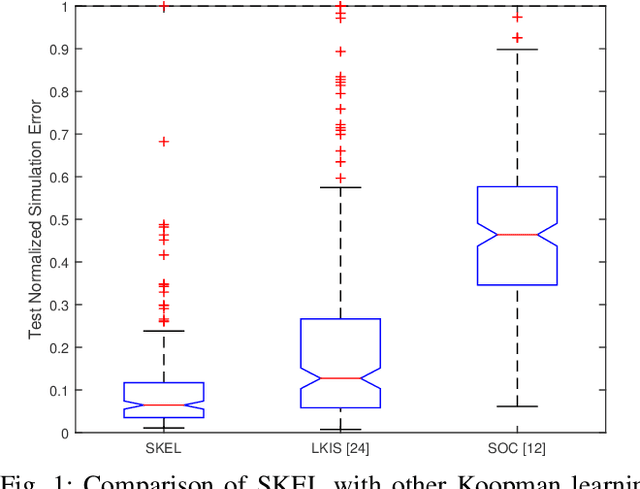
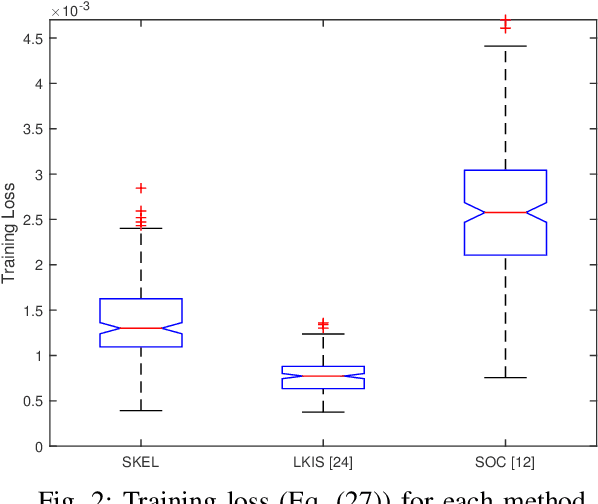
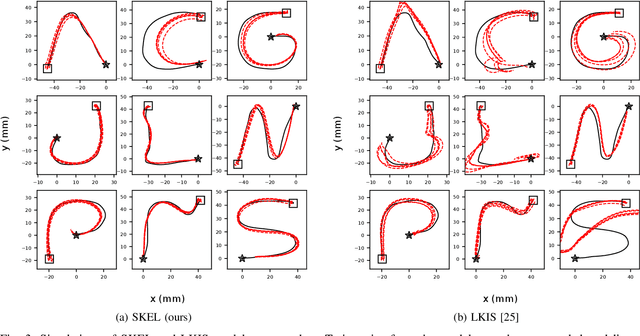
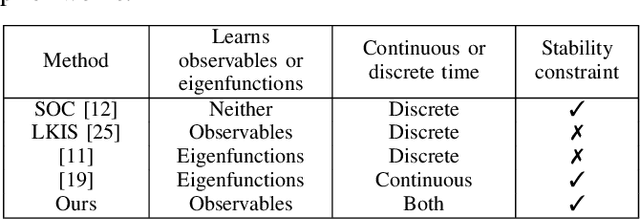
In this paper, we present a new data-driven method for learning stable models of nonlinear systems. Our model lifts the original state space to a higher-dimensional linear manifold using Koopman embeddings. Interestingly, we prove that every discrete-time nonlinear contracting model can be learnt in our framework. Another significant merit of the proposed approach is that it allows for unconstrained optimization over the Koopman embedding and operator jointly while enforcing stability of the model, via a direct parameterization of stable linear systems, greatly simplifying the computations involved. We validate our method on a simulated system and analyze the advantages of our parameterization compared to alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge