Global and Asymptotically Efficient Localization from Range Measurements
Paper and Code
Apr 02, 2022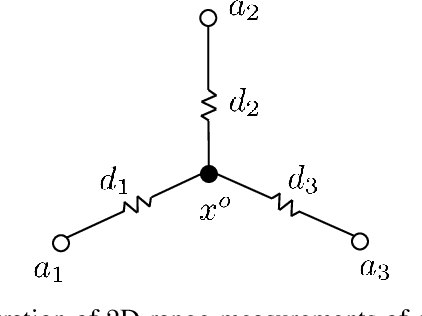
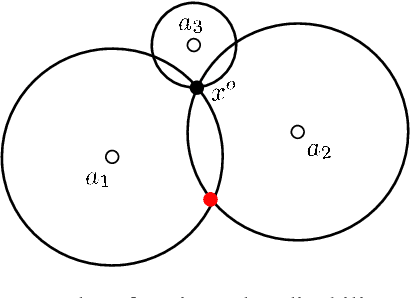
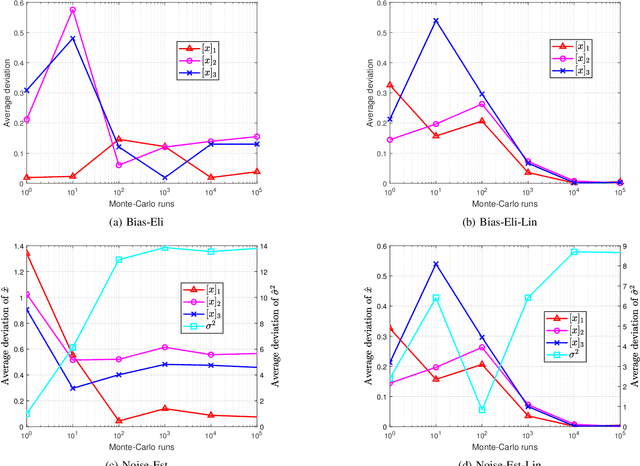
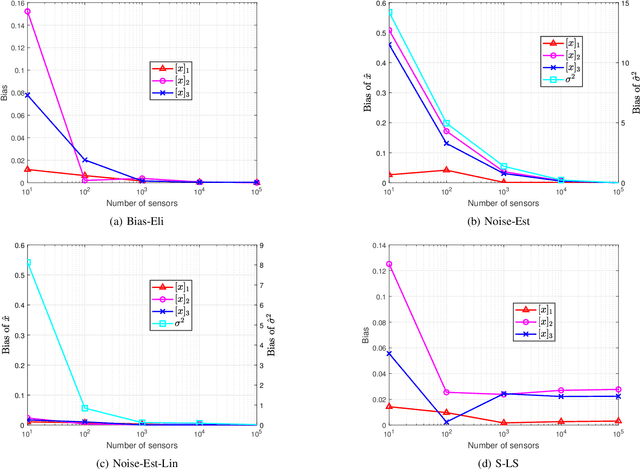
We consider the range-based localization problem, which involves estimating an object's position by using $m$ sensors, hoping that as the number $m$ of sensors increases, the estimate converges to the true position with the minimum variance. We show that under some conditions on the sensor deployment and measurement noises, the LS estimator is strongly consistent and asymptotically normal. However, the LS problem is nonsmooth and nonconvex, and therefore hard to solve. We then devise realizable estimators that possess the same asymptotic properties as the LS one. These estimators are based on a two-step estimation architecture, which says that any $\sqrt{m}$-consistent estimate followed by a one-step Gauss-Newton iteration can yield a solution that possesses the same asymptotic property as the LS one. The keypoint of the two-step scheme is to construct a $\sqrt{m}$-consistent estimate in the first step. In terms of whether the variance of measurement noises is known or not, we propose the Bias-Eli estimator (which involves solving a generalized trust region subproblem) and the Noise-Est estimator (which is obtained by solving a convex problem), respectively. Both of them are proved to be $\sqrt{m}$-consistent. Moreover, we show that by discarding the constraints in the above two optimization problems, the resulting closed-form estimators (called Bias-Eli-Lin and Noise-Est-Lin) are also $\sqrt{m}$-consistent. Plenty of simulations verify the correctness of our theoretical claims, showing that the proposed two-step estimators can asymptotically achieve the Cramer-Rao lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge