Low-complexity Distributed Detection with One-bit Memory Under Neyman-Pearson Criterion
Paper and Code
Apr 22, 2021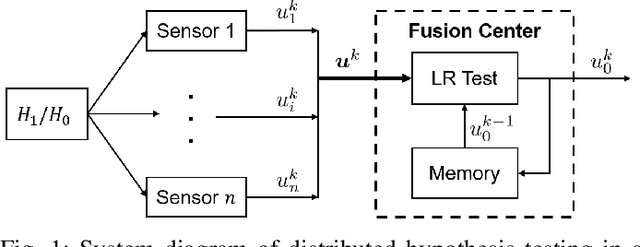
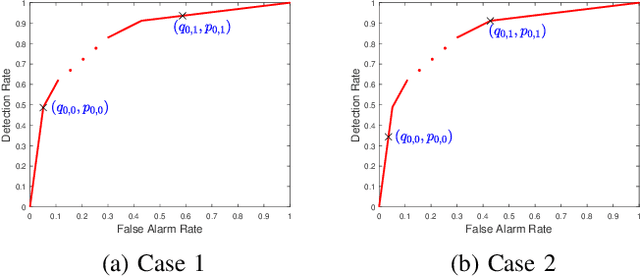
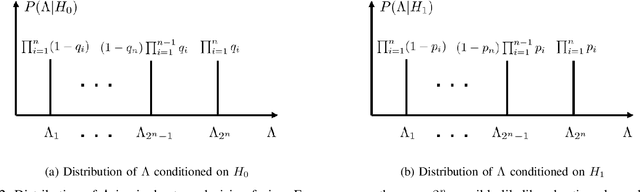
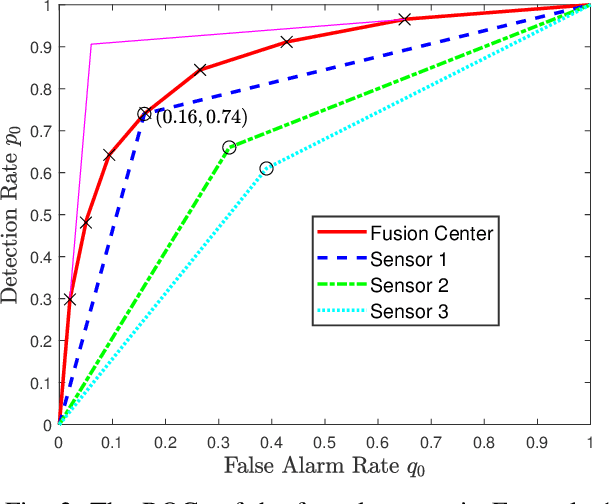
We consider a multi-stage distributed detection scenario, where $n$ sensors and a fusion center (FC) are deployed to accomplish a binary hypothesis test. At each time stage, local sensors generate binary messages, assumed to be spatially and temporally independent given the hypothesis, and then upload them to the FC for global detection decision making. We suppose a one-bit memory is available at the FC to store its decision history and focus on developing iterative fusion schemes. We first visit the detection problem of performing the Neyman-Pearson (N-P) test at each stage and give an optimal algorithm, called the oracle algorithm, to solve it. Structural properties and limitation of the fusion performance in the asymptotic regime are explored for the oracle algorithm. We notice the computational inefficiency of the oracle fusion and propose a low-complexity alternative, for which the likelihood ratio (LR) test threshold is tuned in connection to the fusion decision history compressed in the one-bit memory. The low-complexity algorithm greatly brings down the computational complexity at each stage from $O(4^n)$ to $O(n)$. We show that the proposed algorithm is capable of converging exponentially to the same detection probability as that of the oracle one. Moreover, the rate of convergence is shown to be asymptotically identical to that of the oracle algorithm. Finally, numerical simulations and real-world experiments demonstrate the effectiveness and efficiency of our distributed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge