BESTAnP: Bi-Step Efficient and Statistically Optimal Estimator for Acoustic-n-Point Problem
Paper and Code
Nov 26, 2024
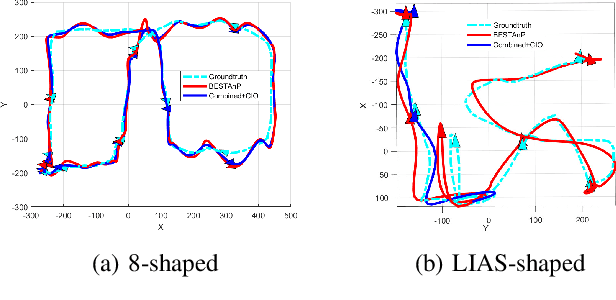
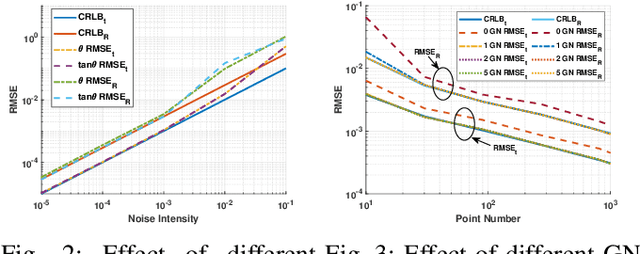
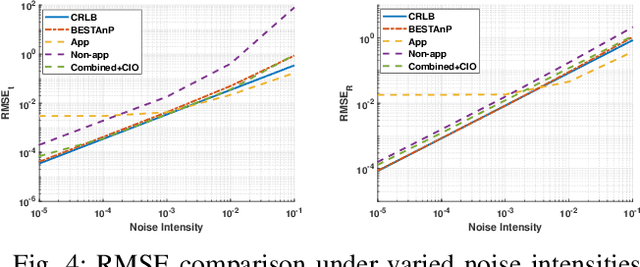
We consider the acoustic-n-point (AnP) problem, which estimates the pose of a 2D forward-looking sonar (FLS) according to n 3D-2D point correspondences. We explore the nature of the measured partial spherical coordinates and reveal their inherent relationships to translation and orientation. Based on this, we propose a bi-step efficient and statistically optimal AnP (BESTAnP) algorithm that decouples the estimation of translation and orientation. Specifically, in the first step, the translation estimation is formulated as the range-based localization problem based on distance-only measurements. In the second step, the rotation is estimated via eigendecomposition based on azimuth-only measurements and the estimated translation. BESTAnP is the first AnP algorithm that gives a closed-form solution for the full six-degree pose. In addition, we conduct bias elimination for BESTAnP such that it owns the statistical property of consistency. Through simulation and real-world experiments, we demonstrate that compared with the state-of-the-art (SOTA) methods, BESTAnP is over ten times faster and features real-time capacity in resource-constrained platforms while exhibiting comparable accuracy. Moreover, for the first time, we embed BESTAnP into a sonar-based odometry which shows its effectiveness for trajectory estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge