Fudong Wang
LangScene-X: Reconstruct Generalizable 3D Language-Embedded Scenes with TriMap Video Diffusion
Jul 03, 2025


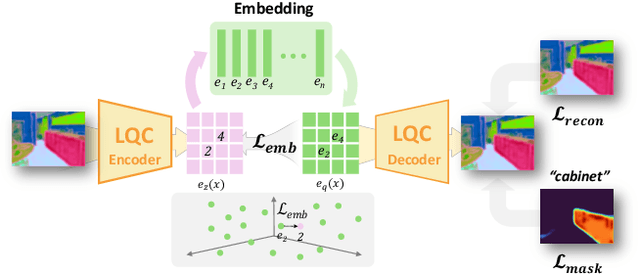
Abstract:Recovering 3D structures with open-vocabulary scene understanding from 2D images is a fundamental but daunting task. Recent developments have achieved this by performing per-scene optimization with embedded language information. However, they heavily rely on the calibrated dense-view reconstruction paradigm, thereby suffering from severe rendering artifacts and implausible semantic synthesis when limited views are available. In this paper, we introduce a novel generative framework, coined LangScene-X, to unify and generate 3D consistent multi-modality information for reconstruction and understanding. Powered by the generative capability of creating more consistent novel observations, we can build generalizable 3D language-embedded scenes from only sparse views. Specifically, we first train a TriMap video diffusion model that can generate appearance (RGBs), geometry (normals), and semantics (segmentation maps) from sparse inputs through progressive knowledge integration. Furthermore, we propose a Language Quantized Compressor (LQC), trained on large-scale image datasets, to efficiently encode language embeddings, enabling cross-scene generalization without per-scene retraining. Finally, we reconstruct the language surface fields by aligning language information onto the surface of 3D scenes, enabling open-ended language queries. Extensive experiments on real-world data demonstrate the superiority of our LangScene-X over state-of-the-art methods in terms of quality and generalizability. Project Page: https://liuff19.github.io/LangScene-X.
Ming-Omni: A Unified Multimodal Model for Perception and Generation
Jun 11, 2025


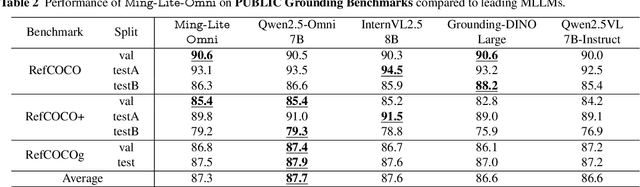
Abstract:We propose Ming-Omni, a unified multimodal model capable of processing images, text, audio, and video, while demonstrating strong proficiency in both speech and image generation. Ming-Omni employs dedicated encoders to extract tokens from different modalities, which are then processed by Ling, an MoE architecture equipped with newly proposed modality-specific routers. This design enables a single model to efficiently process and fuse multimodal inputs within a unified framework, thereby facilitating diverse tasks without requiring separate models, task-specific fine-tuning, or structural redesign. Importantly, Ming-Omni extends beyond conventional multimodal models by supporting audio and image generation. This is achieved through the integration of an advanced audio decoder for natural-sounding speech and Ming-Lite-Uni for high-quality image generation, which also allow the model to engage in context-aware chatting, perform text-to-speech conversion, and conduct versatile image editing. Our experimental results showcase Ming-Omni offers a powerful solution for unified perception and generation across all modalities. Notably, our proposed Ming-Omni is the first open-source model we are aware of to match GPT-4o in modality support, and we release all code and model weights to encourage further research and development in the community.
GraphicsDreamer: Image to 3D Generation with Physical Consistency
Dec 18, 2024



Abstract:Recently, the surge of efficient and automated 3D AI-generated content (AIGC) methods has increasingly illuminated the path of transforming human imagination into complex 3D structures. However, the automated generation of 3D content is still significantly lags in industrial application. This gap exists because 3D modeling demands high-quality assets with sharp geometry, exquisite topology, and physically based rendering (PBR), among other criteria. To narrow the disparity between generated results and artists' expectations, we introduce GraphicsDreamer, a method for creating highly usable 3D meshes from single images. To better capture the geometry and material details, we integrate the PBR lighting equation into our cross-domain diffusion model, concurrently predicting multi-view color, normal, depth images, and PBR materials. In the geometry fusion stage, we continue to enforce the PBR constraints, ensuring that the generated 3D objects possess reliable texture details, supporting realistic relighting. Furthermore, our method incorporates topology optimization and fast UV unwrapping capabilities, allowing the 3D products to be seamlessly imported into graphics engines. Extensive experiments demonstrate that our model can produce high quality 3D assets in a reasonable time cost compared to previous methods.
Learning Canonical View Representation for 3D Shape Recognition with Arbitrary Views
Aug 17, 2021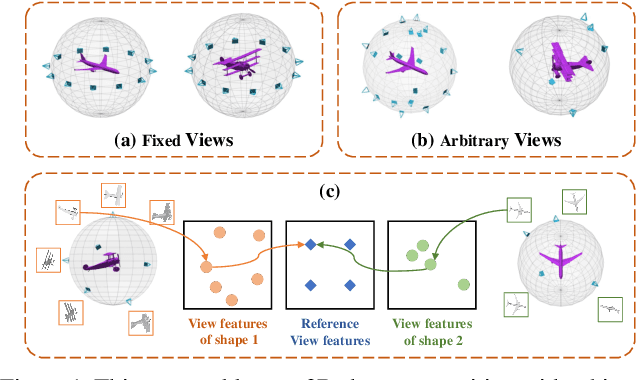

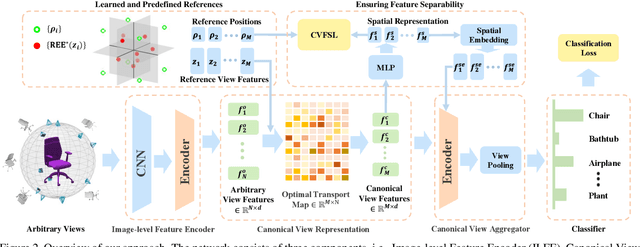

Abstract:In this paper, we focus on recognizing 3D shapes from arbitrary views, i.e., arbitrary numbers and positions of viewpoints. It is a challenging and realistic setting for view-based 3D shape recognition. We propose a canonical view representation to tackle this challenge. We first transform the original features of arbitrary views to a fixed number of view features, dubbed canonical view representation, by aligning the arbitrary view features to a set of learnable reference view features using optimal transport. In this way, each 3D shape with arbitrary views is represented by a fixed number of canonical view features, which are further aggregated to generate a rich and robust 3D shape representation for shape recognition. We also propose a canonical view feature separation constraint to enforce that the view features in canonical view representation can be embedded into scattered points in a Euclidean space. Experiments on the ModelNet40, ScanObjectNN, and RGBD datasets show that our method achieves competitive results under the fixed viewpoint settings, and significantly outperforms the applicable methods under the arbitrary view setting.
Deep Graph Matching under Quadratic Constraint
Mar 14, 2021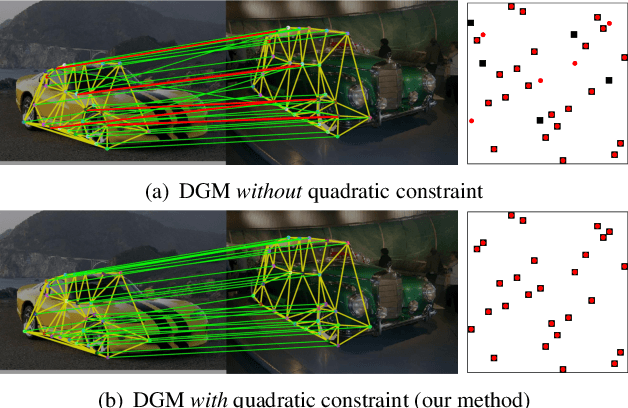
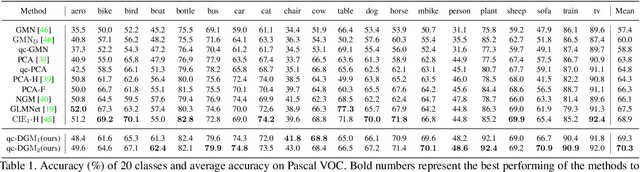
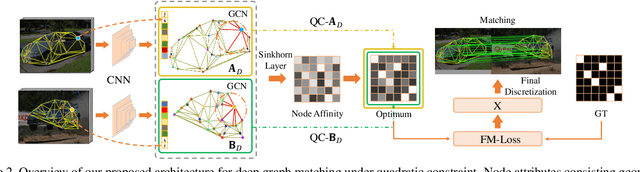

Abstract:Recently, deep learning based methods have demonstrated promising results on the graph matching problem, by relying on the descriptive capability of deep features extracted on graph nodes. However, one main limitation with existing deep graph matching (DGM) methods lies in their ignorance of explicit constraint of graph structures, which may lead the model to be trapped into local minimum in training. In this paper, we propose to explicitly formulate pairwise graph structures as a \textbf{quadratic constraint} incorporated into the DGM framework. The quadratic constraint minimizes the pairwise structural discrepancy between graphs, which can reduce the ambiguities brought by only using the extracted CNN features. Moreover, we present a differentiable implementation to the quadratic constrained-optimization such that it is compatible with the unconstrained deep learning optimizer. To give more precise and proper supervision, a well-designed false matching loss against class imbalance is proposed, which can better penalize the false negatives and false positives with less overfitting. Exhaustive experiments demonstrate that our method competitive performance on real-world datasets.
Zero-Assignment Constraint for Graph Matching with Outliers
Mar 26, 2020
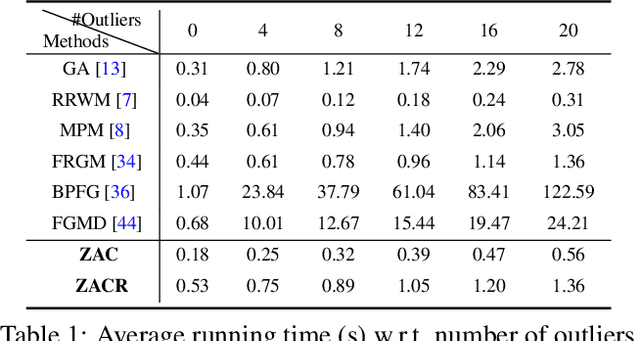

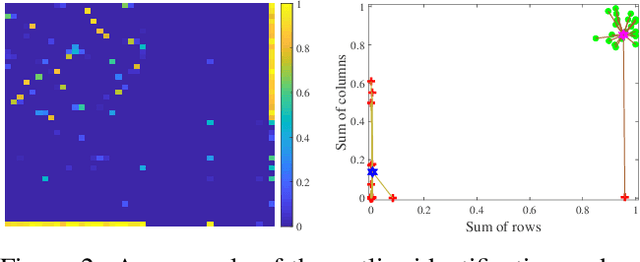
Abstract:Graph matching (GM), as a longstanding problem in computer vision and pattern recognition, still suffers from numerous cluttered outliers in practical applications. To address this issue, we present the zero-assignment constraint (ZAC) for approaching the graph matching problem in the presence of outliers. The underlying idea is to suppress the matchings of outliers by assigning zero-valued vectors to the potential outliers in the obtained optimal correspondence matrix. We provide elaborate theoretical analysis to the problem, i.e., GM with ZAC, and figure out that the GM problem with and without outliers are intrinsically different, which enables us to put forward a sufficient condition to construct valid and reasonable objective function. Consequently, we design an efficient outlier-robust algorithm to significantly reduce the incorrect or redundant matchings caused by numerous outliers. Extensive experiments demonstrate that our method can achieve the state-of-the-art performance in terms of accuracy and efficiency, especially in the presence of numerous outliers.
Learning Attraction Field Representation for Robust Line Segment Detection
Dec 05, 2018

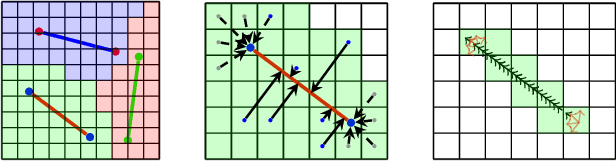
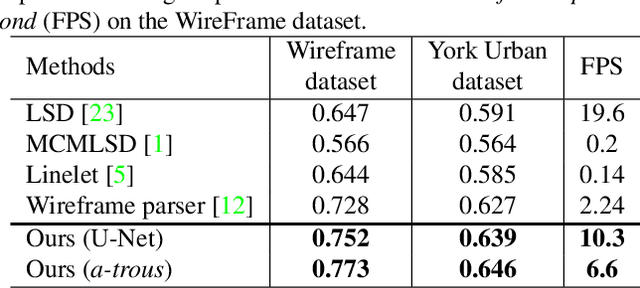
Abstract:This paper presents a region-partition based attraction field dual representation for line segment maps, and thus poses the problem of line segment detection (LSD) as the region coloring problem. The latter is then addressed by learning deep convolutional neural networks (ConvNets) for accuracy, robustness and efficiency. For a 2D line segment map, our dual representation consists of three components: (i) A region-partition map in which every pixel is assigned to one and only one line segment; (ii) An attraction field map in which every pixel in a partition region is encoded by its 2D projection vector w.r.t. the associated line segment; and (iii) A squeeze module which squashes the attraction field to a line segment map that almost perfectly recovers the input one. By leveraging the duality, we learn ConvNets to compute the attraction field maps for raw in-put images, followed by the squeeze module for LSD, in an end-to-end manner. Our method rigorously addresses several challenges in LSD such as local ambiguity and class imbalance. Our method also harnesses the best practices developed in ConvNets based semantic segmentation methods such as the encoder-decoder architecture and the a-trous convolution. In experiments, our method is tested on the WireFrame dataset and the YorkUrban dataset with state-of-the-art performance obtained. Especially, we advance the performance by 4.5 percents on the WireFrame dataset. Our method is also fast with 6.6~10.4 FPS, outperforming most of existing line segment detectors.
Adaptively Transforming Graph Matching
Jul 26, 2018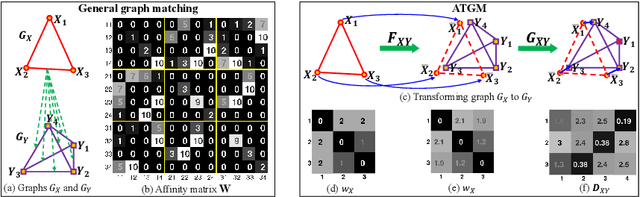
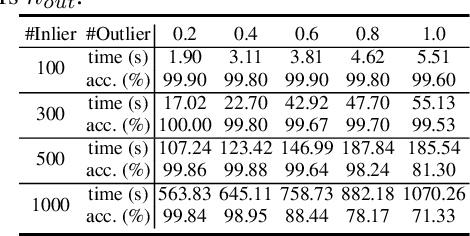

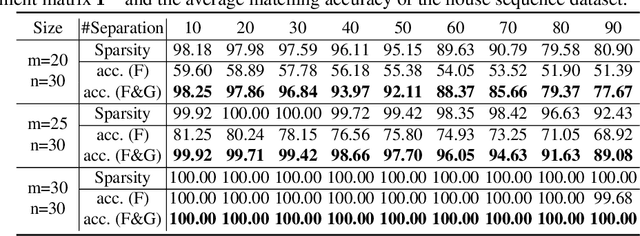
Abstract:Recently, many graph matching methods that incorporate pairwise constraint and that can be formulated as a quadratic assignment problem (QAP) have been proposed. Although these methods demonstrate promising results for the graph matching problem, they have high complexity in space or time. In this paper, we introduce an adaptively transforming graph matching (ATGM) method from the perspective of functional representation. More precisely, under a transformation formulation, we aim to match two graphs by minimizing the discrepancy between the original graph and the transformed graph. With a linear representation map of the transformation, the pairwise edge attributes of graphs are explicitly represented by unary node attributes, which enables us to reduce the space and time complexity significantly. Due to an efficient Frank-Wolfe method-based optimization strategy, we can handle graphs with hundreds and thousands of nodes within an acceptable amount of time. Meanwhile, because transformation map can preserve graph structures, a domain adaptation-based strategy is proposed to remove the outliers. The experimental results demonstrate that our proposed method outperforms the state-of-the-art graph matching algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge