Adaptively Transforming Graph Matching
Paper and Code
Jul 26, 2018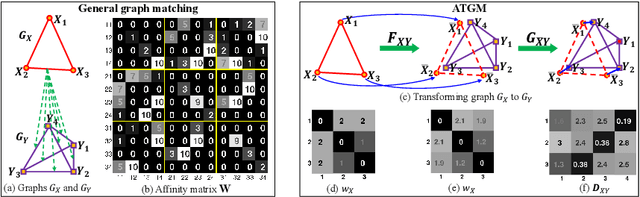
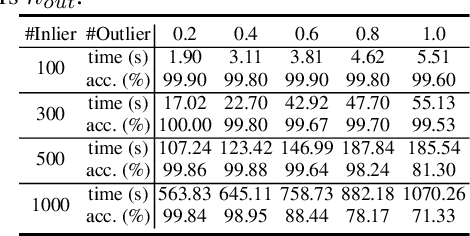

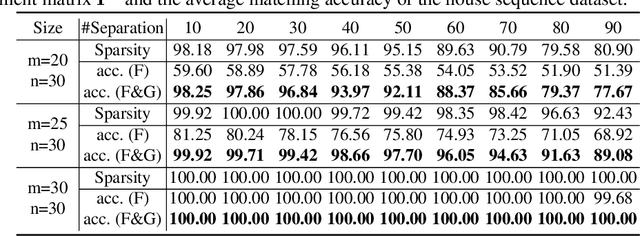
Recently, many graph matching methods that incorporate pairwise constraint and that can be formulated as a quadratic assignment problem (QAP) have been proposed. Although these methods demonstrate promising results for the graph matching problem, they have high complexity in space or time. In this paper, we introduce an adaptively transforming graph matching (ATGM) method from the perspective of functional representation. More precisely, under a transformation formulation, we aim to match two graphs by minimizing the discrepancy between the original graph and the transformed graph. With a linear representation map of the transformation, the pairwise edge attributes of graphs are explicitly represented by unary node attributes, which enables us to reduce the space and time complexity significantly. Due to an efficient Frank-Wolfe method-based optimization strategy, we can handle graphs with hundreds and thousands of nodes within an acceptable amount of time. Meanwhile, because transformation map can preserve graph structures, a domain adaptation-based strategy is proposed to remove the outliers. The experimental results demonstrate that our proposed method outperforms the state-of-the-art graph matching algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge