Up-sampling-only and Adaptive Mesh-based GNN for Simulating Physical Systems

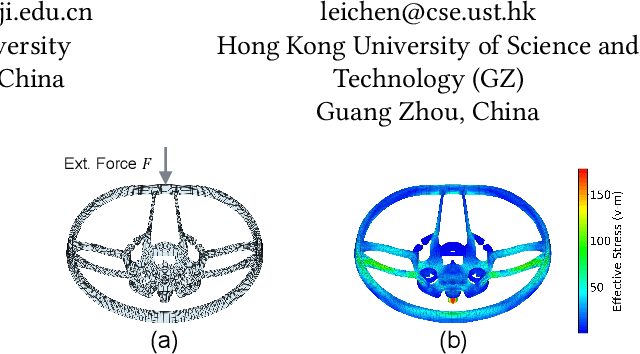
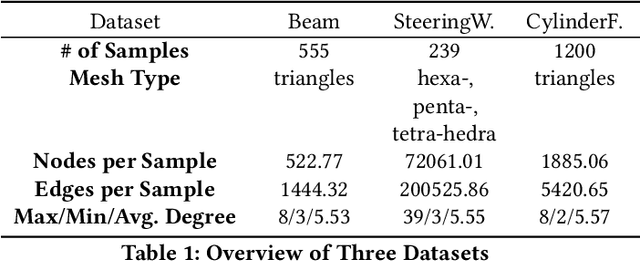
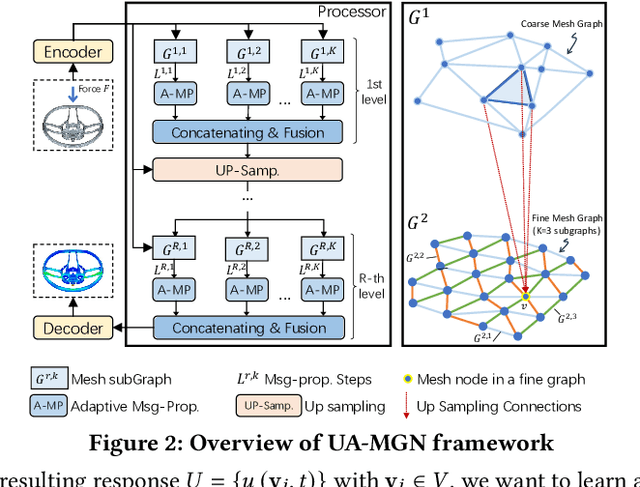
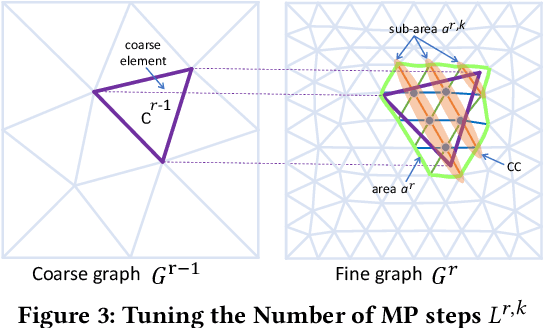
Traditional simulation of complex mechanical systems relies on numerical solvers of Partial Differential Equations (PDEs), e.g., using the Finite Element Method (FEM). The FEM solvers frequently suffer from intensive computation cost and high running time. Recent graph neural network (GNN)-based simulation models can improve running time meanwhile with acceptable accuracy. Unfortunately, they are hard to tailor GNNs for complex mechanical systems, including such disadvantages as ineffective representation and inefficient message propagation (MP). To tackle these issues, in this paper, with the proposed Up-sampling-only and Adaptive MP techniques, we develop a novel hierarchical Mesh Graph Network, namely UA-MGN, for efficient and effective mechanical simulation. Evaluation on two synthetic and one real datasets demonstrates the superiority of the UA-MGN. For example, on the Beam dataset, compared to the state-of-the-art MS-MGN, UA-MGN leads to 40.99% lower errors but using only 43.48% fewer network parameters and 4.49% fewer floating point operations (FLOPs).

Learning-Based Finite Element Methods Modeling for Complex Mechanical Systems

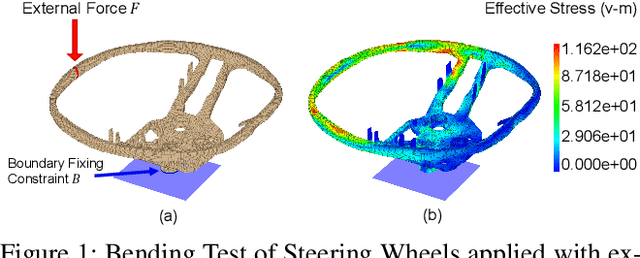
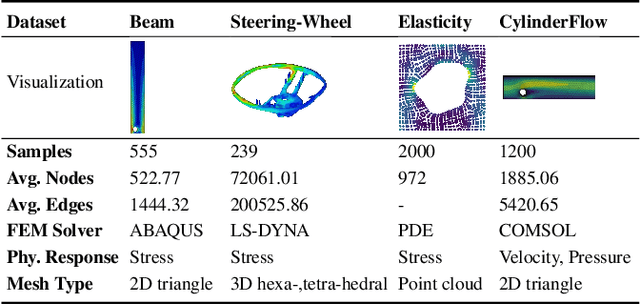
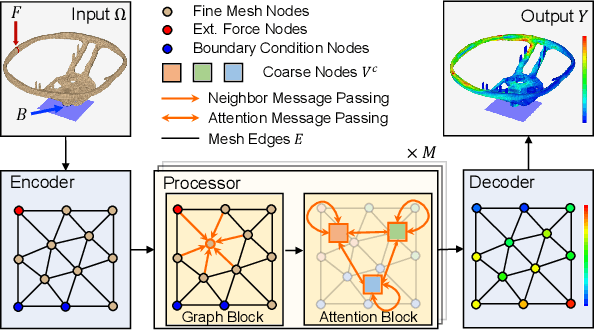
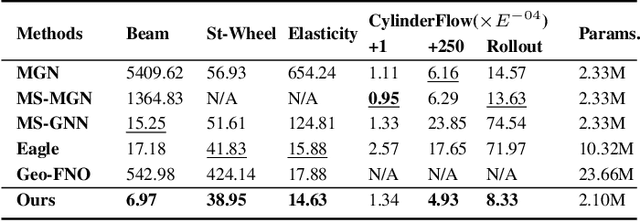
Complex mechanic systems simulation is important in many real-world applications. The de-facto numeric solver using Finite Element Method (FEM) suffers from computationally intensive overhead. Though with many progress on the reduction of computational time and acceptable accuracy, the recent CNN or GNN-based simulation models still struggle to effectively represent complex mechanic simulation caused by the long-range spatial dependency of distance mesh nodes and independently learning local and global representation. In this paper, we propose a novel two-level mesh graph network. The key of the network is to interweave the developed Graph Block and Attention Block to better learn mechanic interactions even for long-rang spatial dependency. Evaluation on three synthetic and one real datasets demonstrates the superiority of our work. For example, on the Beam dataset, our work leads to 54.3\% lower prediction errors and 9.87\% fewer learnable network parameters.

Imbalanced Graph-Level Anomaly Detection via Counterfactual Augmentation and Feature Learning

Graph-level anomaly detection (GLAD) has already gained significant importance and has become a popular field of study, attracting considerable attention across numerous downstream works. The core focus of this domain is to capture and highlight the anomalous information within given graph datasets. In most existing studies, anomalies are often the instances of few. The stark imbalance misleads current GLAD methods to focus on learning the patterns of normal graphs more, further impacting anomaly detection performance. Moreover, existing methods predominantly utilize the inherent features of nodes to identify anomalous graph patterns which is approved suboptimal according to our experiments. In this work, we propose an imbalanced GLAD method via counterfactual augmentation and feature learning. Specifically, we first construct anomalous samples based on counterfactual learning, aiming to expand and balance the datasets. Additionally, we construct a module based on Graph Neural Networks (GNNs), which allows us to utilize degree attributes to complement the inherent attribute features of nodes. Then, we design an adaptive weight learning module to integrate features tailored to different datasets effectively to avoid indiscriminately treating all features as equivalent. Furthermore, extensive baseline experiments conducted on public datasets substantiate the robustness and effectiveness. Besides, we apply the model to brain disease datasets, which can prove the generalization capability of our work. The source code of our work is available online.

Discriminative Graph-level Anomaly Detection via Dual-students-teacher Model

Different from the current node-level anomaly detection task, the goal of graph-level anomaly detection is to find abnormal graphs that significantly differ from others in a graph set. Due to the scarcity of research on the work of graph-level anomaly detection, the detailed description of graph-level anomaly is insufficient. Furthermore, existing works focus on capturing anomalous graph information to learn better graph representations, but they ignore the importance of an effective anomaly score function for evaluating abnormal graphs. Thus, in this work, we first define anomalous graph information including node and graph property anomalies in a graph set and adopt node-level and graph-level information differences to identify them, respectively. Then, we introduce a discriminative graph-level anomaly detection framework with dual-students-teacher model, where the teacher model with a heuristic loss are trained to make graph representations more divergent. Then, two competing student models trained by normal and abnormal graphs respectively fit graph representations of the teacher model in terms of node-level and graph-level representation perspectives. Finally, we combine representation errors between two student models to discriminatively distinguish anomalous graphs. Extensive experiment analysis demonstrates that our method is effective for the graph-level anomaly detection task on graph datasets in the real world.

Multi-representations Space Separation based Graph-level Anomaly-aware Detection

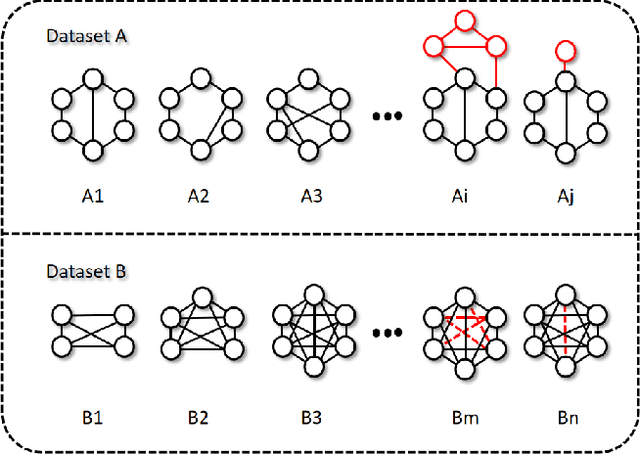
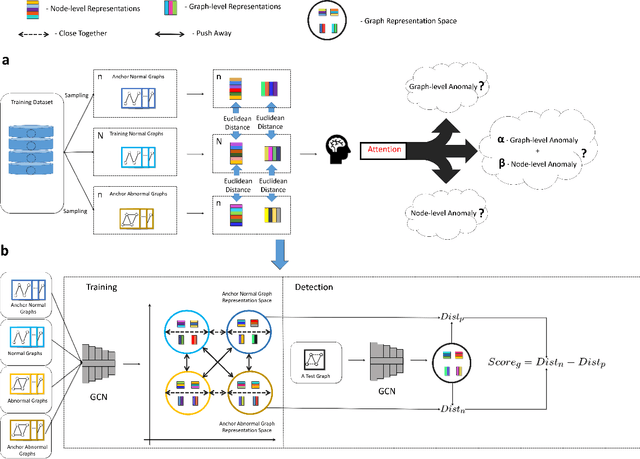
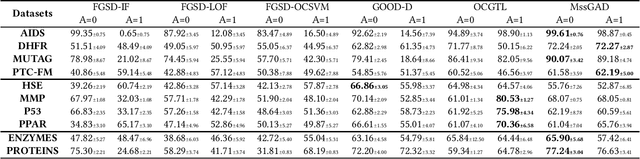
Graph structure patterns are widely used to model different area data recently. How to detect anomalous graph information on these graph data has become a popular research problem. The objective of this research is centered on the particular issue that how to detect abnormal graphs within a graph set. The previous works have observed that abnormal graphs mainly show node-level and graph-level anomalies, but these methods equally treat two anomaly forms above in the evaluation of abnormal graphs, which is contrary to the fact that different types of abnormal graph data have different degrees in terms of node-level and graph-level anomalies. Furthermore, abnormal graphs that have subtle differences from normal graphs are easily escaped detection by the existing methods. Thus, we propose a multi-representations space separation based graph-level anomaly-aware detection framework in this paper. To consider the different importance of node-level and graph-level anomalies, we design an anomaly-aware module to learn the specific weight between them in the abnormal graph evaluation process. In addition, we learn strictly separate normal and abnormal graph representation spaces by four types of weighted graph representations against each other including anchor normal graphs, anchor abnormal graphs, training normal graphs, and training abnormal graphs. Based on the distance error between the graph representations of the test graph and both normal and abnormal graph representation spaces, we can accurately determine whether the test graph is anomalous. Our approach has been extensively evaluated against baseline methods using ten public graph datasets, and the results demonstrate its effectiveness.

Prompt-Learning for Cross-Lingual Relation Extraction

Relation Extraction (RE) is a crucial task in Information Extraction, which entails predicting relationships between entities within a given sentence. However, extending pre-trained RE models to other languages is challenging, particularly in real-world scenarios where Cross-Lingual Relation Extraction (XRE) is required. Despite recent advancements in Prompt-Learning, which involves transferring knowledge from Multilingual Pre-trained Language Models (PLMs) to diverse downstream tasks, there is limited research on the effective use of multilingual PLMs with prompts to improve XRE. In this paper, we present a novel XRE algorithm based on Prompt-Tuning, referred to as Prompt-XRE. To evaluate its effectiveness, we design and implement several prompt templates, including hard, soft, and hybrid prompts, and empirically test their performance on competitive multilingual PLMs, specifically mBART. Our extensive experiments, conducted on the low-resource ACE05 benchmark across multiple languages, demonstrate that our Prompt-XRE algorithm significantly outperforms both vanilla multilingual PLMs and other existing models, achieving state-of-the-art performance in XRE. To further show the generalization of our Prompt-XRE on larger data scales, we construct and release a new XRE dataset- WMT17-EnZh XRE, containing 0.9M English-Chinese pairs extracted from WMT 2017 parallel corpus. Experiments on WMT17-EnZh XRE also show the effectiveness of our Prompt-XRE against other competitive baselines. The code and newly constructed dataset are freely available at \url{https://github.com/HSU-CHIA-MING/Prompt-XRE}.

Likelihood Landscapes: A Unifying Principle Behind Many Adversarial Defenses

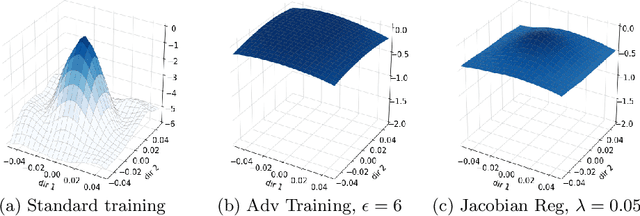
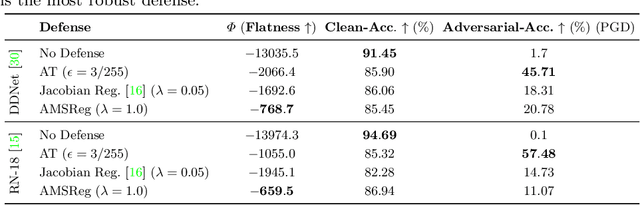
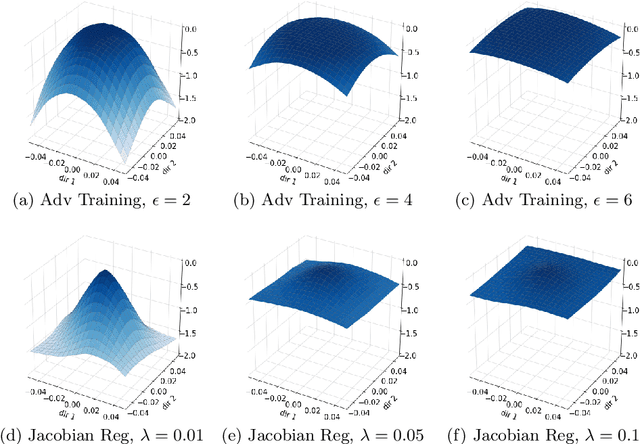
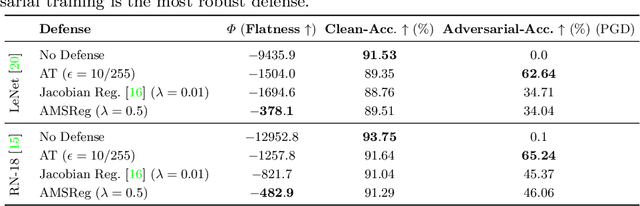
Convolutional Neural Networks have been shown to be vulnerable to adversarial examples, which are known to locate in subspaces close to where normal data lies but are not naturally occurring and of low probability. In this work, we investigate the potential effect defense techniques have on the geometry of the likelihood landscape - likelihood of the input images under the trained model. We first propose a way to visualize the likelihood landscape leveraging an energy-based model interpretation of discriminative classifiers. Then we introduce a measure to quantify the flatness of the likelihood landscape. We observe that a subset of adversarial defense techniques results in a similar effect of flattening the likelihood landscape. We further explore directly regularizing towards a flat landscape for adversarial robustness.

Algorithms for leader selection in stochastically forced consensus networks

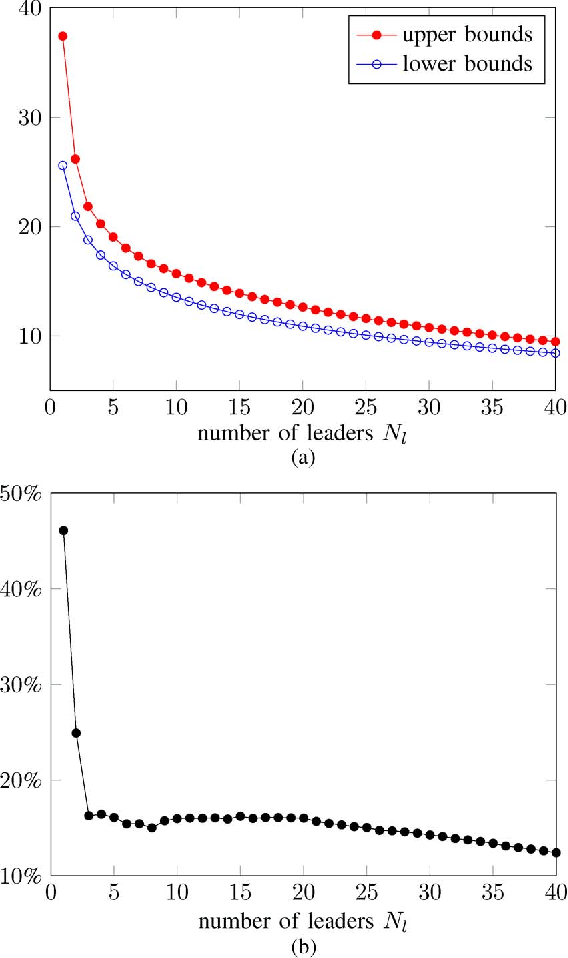
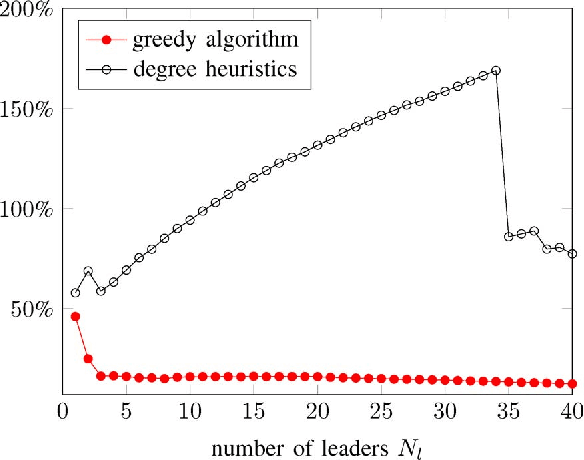
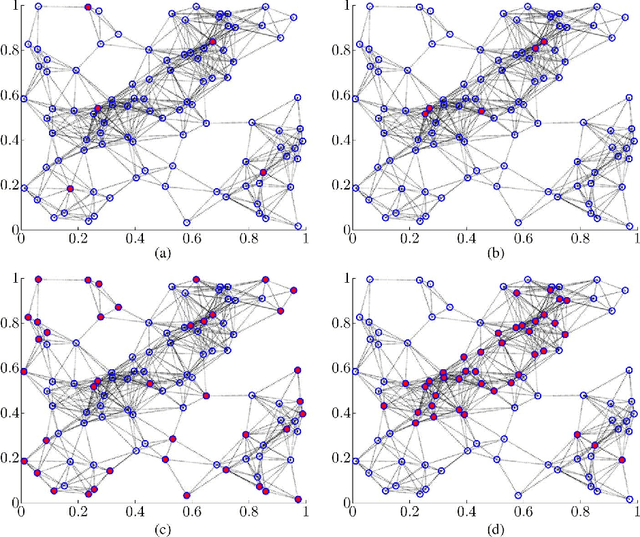
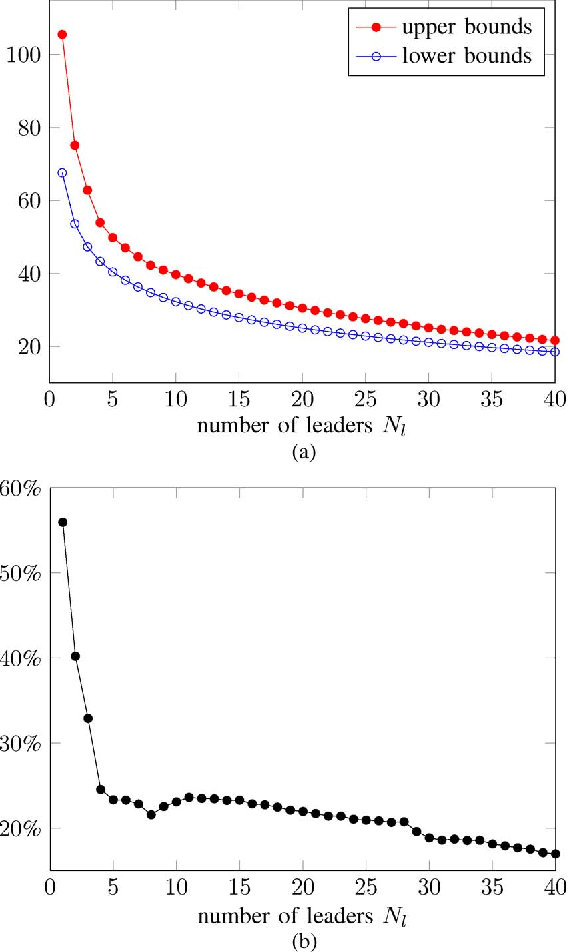
We are interested in assigning a pre-specified number of nodes as leaders in order to minimize the mean-square deviation from consensus in stochastically forced networks. This problem arises in several applications including control of vehicular formations and localization in sensor networks. For networks with leaders subject to noise, we show that the Boolean constraints (a node is either a leader or it is not) are the only source of nonconvexity. By relaxing these constraints to their convex hull we obtain a lower bound on the global optimal value. We also use a simple but efficient greedy algorithm to identify leaders and to compute an upper bound. For networks with leaders that perfectly follow their desired trajectories, we identify an additional source of nonconvexity in the form of a rank constraint. Removal of the rank constraint and relaxation of the Boolean constraints yields a semidefinite program for which we develop a customized algorithm well-suited for large networks. Several examples ranging from regular lattices to random graphs are provided to illustrate the effectiveness of the developed algorithms.