Up-sampling-only and Adaptive Mesh-based GNN for Simulating Physical Systems

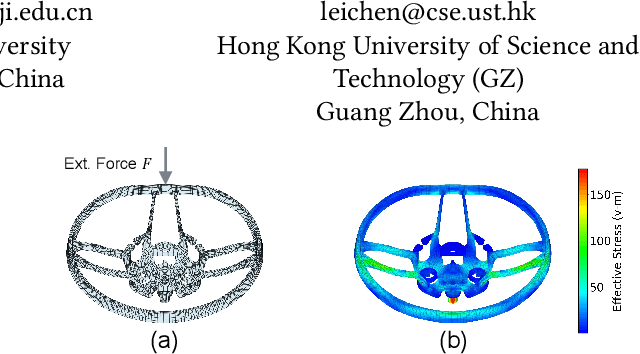
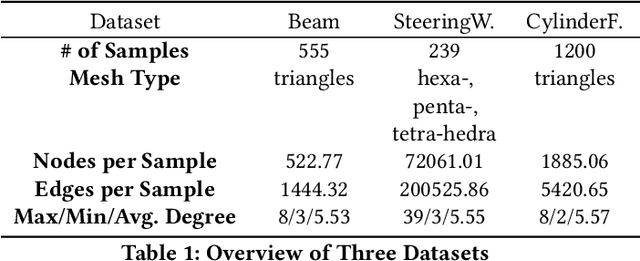
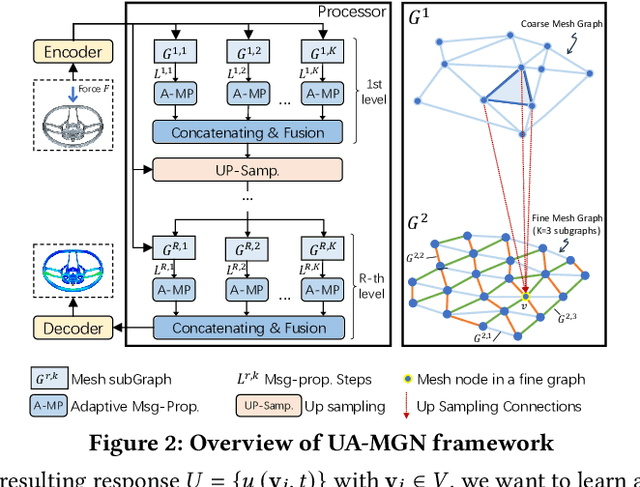
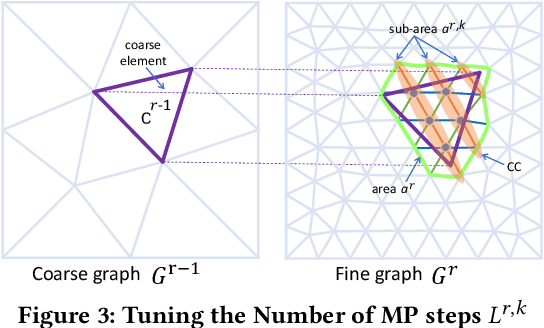
Traditional simulation of complex mechanical systems relies on numerical solvers of Partial Differential Equations (PDEs), e.g., using the Finite Element Method (FEM). The FEM solvers frequently suffer from intensive computation cost and high running time. Recent graph neural network (GNN)-based simulation models can improve running time meanwhile with acceptable accuracy. Unfortunately, they are hard to tailor GNNs for complex mechanical systems, including such disadvantages as ineffective representation and inefficient message propagation (MP). To tackle these issues, in this paper, with the proposed Up-sampling-only and Adaptive MP techniques, we develop a novel hierarchical Mesh Graph Network, namely UA-MGN, for efficient and effective mechanical simulation. Evaluation on two synthetic and one real datasets demonstrates the superiority of the UA-MGN. For example, on the Beam dataset, compared to the state-of-the-art MS-MGN, UA-MGN leads to 40.99% lower errors but using only 43.48% fewer network parameters and 4.49% fewer floating point operations (FLOPs).

Learning-Based Finite Element Methods Modeling for Complex Mechanical Systems

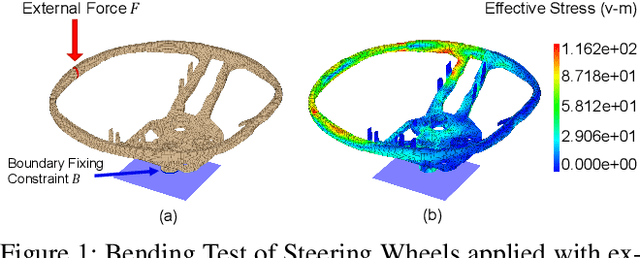
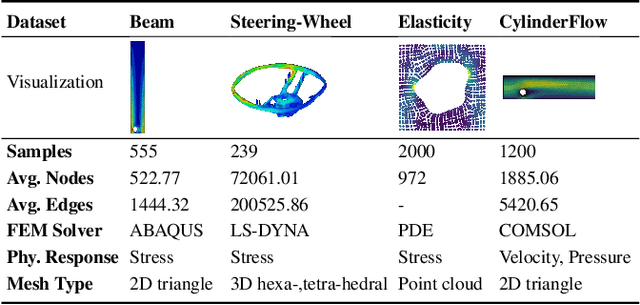
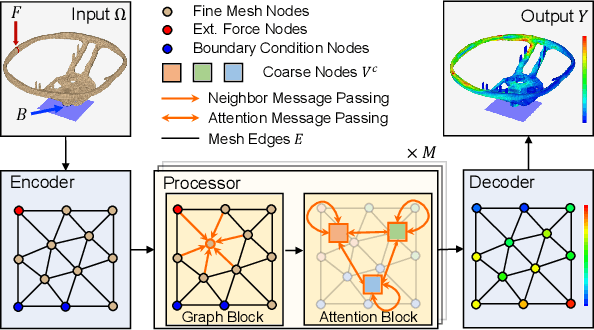
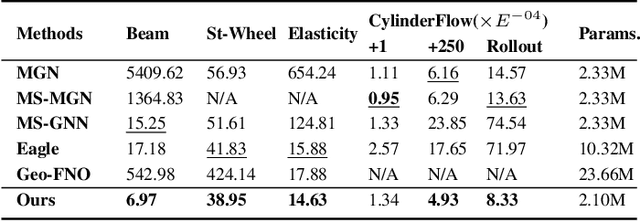
Complex mechanic systems simulation is important in many real-world applications. The de-facto numeric solver using Finite Element Method (FEM) suffers from computationally intensive overhead. Though with many progress on the reduction of computational time and acceptable accuracy, the recent CNN or GNN-based simulation models still struggle to effectively represent complex mechanic simulation caused by the long-range spatial dependency of distance mesh nodes and independently learning local and global representation. In this paper, we propose a novel two-level mesh graph network. The key of the network is to interweave the developed Graph Block and Attention Block to better learn mechanic interactions even for long-rang spatial dependency. Evaluation on three synthetic and one real datasets demonstrates the superiority of our work. For example, on the Beam dataset, our work leads to 54.3\% lower prediction errors and 9.87\% fewer learnable network parameters.

Semisupervised score based matching algorithm to evaluate the effect of public health interventions

Multivariate matching algorithms "pair" similar study units in an observational study to remove potential bias and confounding effects caused by the absence of randomizations. In one-to-one multivariate matching algorithms, a large number of "pairs" to be matched could mean both the information from a large sample and a large number of tasks, and therefore, to best match the pairs, such a matching algorithm with efficiency and comparatively limited auxiliary matching knowledge provided through a "training" set of paired units by domain experts, is practically intriguing. We proposed a novel one-to-one matching algorithm based on a quadratic score function $S_{\beta}(x_i,x_j)= \beta^T (x_i-x_j)(x_i-x_j)^T \beta$. The weights $\beta$, which can be interpreted as a variable importance measure, are designed to minimize the score difference between paired training units while maximizing the score difference between unpaired training units. Further, in the typical but intricate case where the training set is much smaller than the unpaired set, we propose a \underline{s}emisupervised \underline{c}ompanion \underline{o}ne-\underline{t}o-\underline{o}ne \underline{m}atching \underline{a}lgorithm (SCOTOMA) that makes the best use of the unpaired units. The proposed weight estimator is proved to be consistent when the truth matching criterion is indeed the quadratic score function. When the model assumptions are violated, we demonstrate that the proposed algorithm still outperforms some popular competing matching algorithms through a series of simulations. We applied the proposed algorithm to a real-world study to investigate the effect of in-person schooling on community Covid-19 transmission rate for policy making purpose.