Transfer learning via Regularized Linear Discriminant Analysis

Linear discriminant analysis is a widely used method for classification. However, the high dimensionality of predictors combined with small sample sizes often results in large classification errors. To address this challenge, it is crucial to leverage data from related source models to enhance the classification performance of a target model. We propose to address this problem in the framework of transfer learning. In this paper, we present novel transfer learning methods via regularized random-effects linear discriminant analysis, where the discriminant direction is estimated as a weighted combination of ridge estimates obtained from both the target and source models. Multiple strategies for determining these weights are introduced and evaluated, including one that minimizes the estimation risk of the discriminant vector and another that minimizes the classification error. Utilizing results from random matrix theory, we explicitly derive the asymptotic values of these weights and the associated classification error rates in the high-dimensional setting, where $p/n \rightarrow \gamma$, with $p$ representing the predictor dimension and $n$ the sample size. We also provide geometric interpretations of various weights and a guidance on which weights to choose. Extensive numerical studies, including simulations and analysis of proteomics-based 10-year cardiovascular disease risk classification, demonstrate the effectiveness of the proposed approach.

Semisupervised score based matching algorithm to evaluate the effect of public health interventions

Multivariate matching algorithms "pair" similar study units in an observational study to remove potential bias and confounding effects caused by the absence of randomizations. In one-to-one multivariate matching algorithms, a large number of "pairs" to be matched could mean both the information from a large sample and a large number of tasks, and therefore, to best match the pairs, such a matching algorithm with efficiency and comparatively limited auxiliary matching knowledge provided through a "training" set of paired units by domain experts, is practically intriguing. We proposed a novel one-to-one matching algorithm based on a quadratic score function $S_{\beta}(x_i,x_j)= \beta^T (x_i-x_j)(x_i-x_j)^T \beta$. The weights $\beta$, which can be interpreted as a variable importance measure, are designed to minimize the score difference between paired training units while maximizing the score difference between unpaired training units. Further, in the typical but intricate case where the training set is much smaller than the unpaired set, we propose a \underline{s}emisupervised \underline{c}ompanion \underline{o}ne-\underline{t}o-\underline{o}ne \underline{m}atching \underline{a}lgorithm (SCOTOMA) that makes the best use of the unpaired units. The proposed weight estimator is proved to be consistent when the truth matching criterion is indeed the quadratic score function. When the model assumptions are violated, we demonstrate that the proposed algorithm still outperforms some popular competing matching algorithms through a series of simulations. We applied the proposed algorithm to a real-world study to investigate the effect of in-person schooling on community Covid-19 transmission rate for policy making purpose.

Bias of AI-Generated Content: An Examination of News Produced by Large Language Models

Large language models (LLMs) have the potential to transform our lives and work through the content they generate, known as AI-Generated Content (AIGC). To harness this transformation, we need to understand the limitations of LLMs. Here, we investigate the bias of AIGC produced by seven representative LLMs, including ChatGPT and LLaMA. We collect news articles from The New York Times and Reuters, both known for their dedication to provide unbiased news. We then apply each examined LLM to generate news content with headlines of these news articles as prompts, and evaluate the gender and racial biases of the AIGC produced by the LLM by comparing the AIGC and the original news articles. We further analyze the gender bias of each LLM under biased prompts by adding gender-biased messages to prompts constructed from these news headlines. Our study reveals that the AIGC produced by each examined LLM demonstrates substantial gender and racial biases. Moreover, the AIGC generated by each LLM exhibits notable discrimination against females and individuals of the Black race. Among the LLMs, the AIGC generated by ChatGPT demonstrates the lowest level of bias, and ChatGPT is the sole model capable of declining content generation when provided with biased prompts.

Proactive Resource Request for Disaster Response: A Deep Learning-based Optimization Model

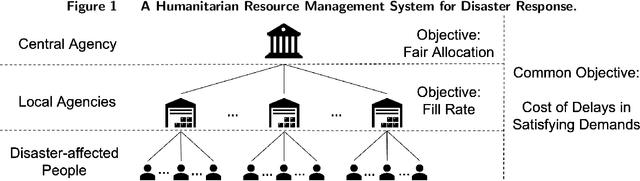
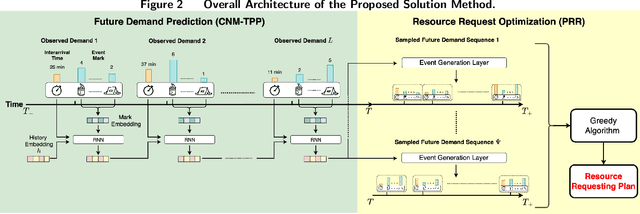
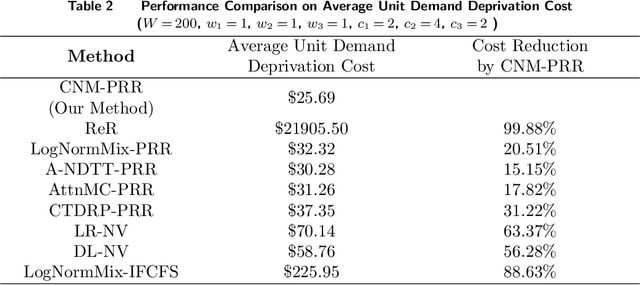
Disaster response is critical to save lives and reduce damages in the aftermath of a disaster. Fundamental to disaster response operations is the management of disaster relief resources. To this end, a local agency (e.g., a local emergency resource distribution center) collects demands from local communities affected by a disaster, dispatches available resources to meet the demands, and requests more resources from a central emergency management agency (e.g., Federal Emergency Management Agency in the U.S.). Prior resource management research for disaster response overlooks the problem of deciding optimal quantities of resources requested by a local agency. In response to this research gap, we define a new resource management problem that proactively decides optimal quantities of requested resources by considering both currently unfulfilled demands and future demands. To solve the problem, we take salient characteristics of the problem into consideration and develop a novel deep learning method for future demand prediction. We then formulate the problem as a stochastic optimization model, analyze key properties of the model, and propose an effective solution method to the problem based on the analyzed properties. We demonstrate the superior performance of our method over prevalent existing methods using both real world and simulated data. We also show its superiority over prevalent existing methods in a multi-stakeholder and multi-objective setting through simulations.

Transfer Learning with Random Coefficient Ridge Regression

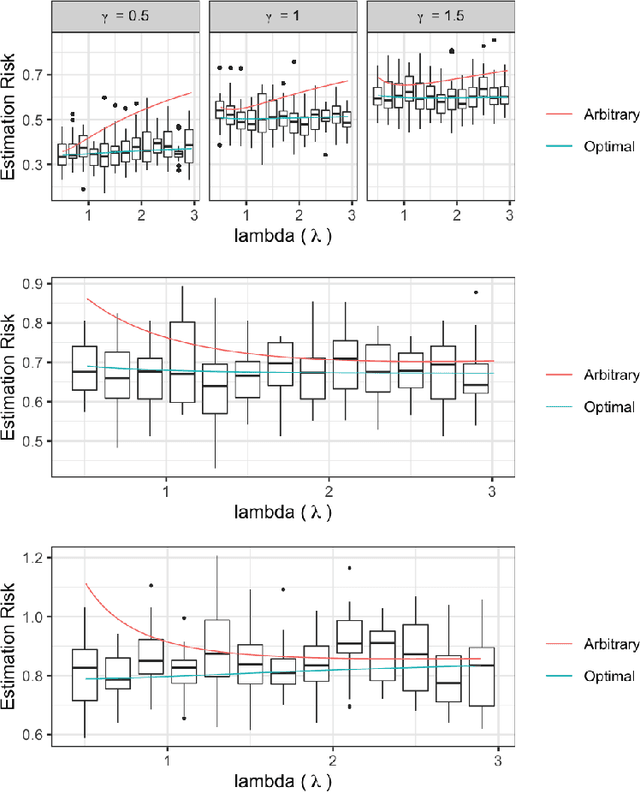
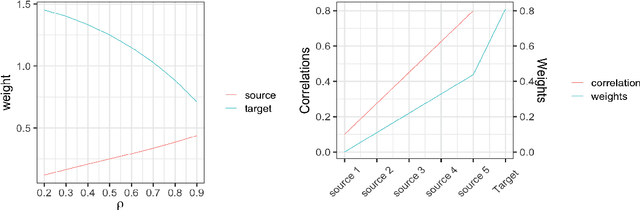
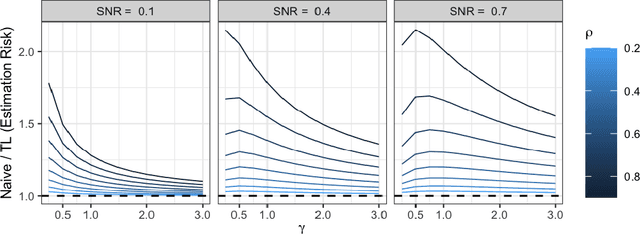
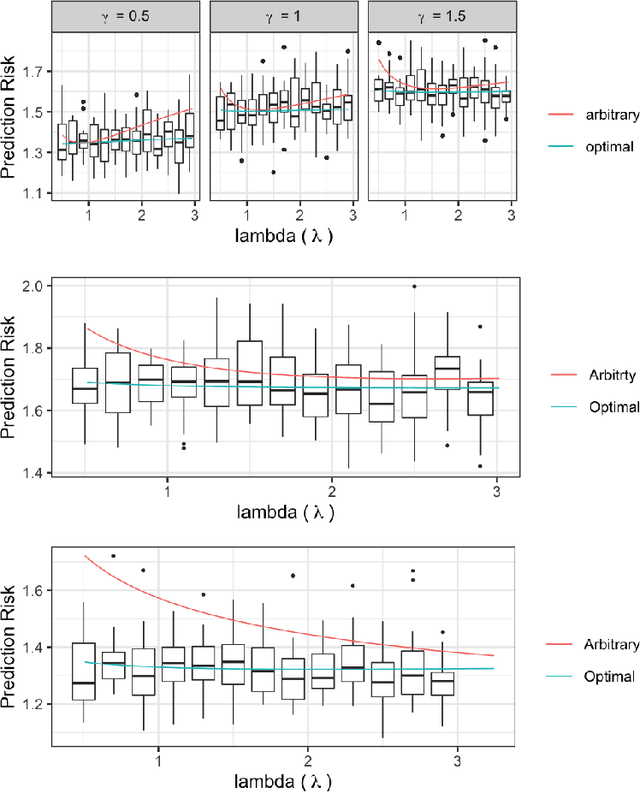
Ridge regression with random coefficients provides an important alternative to fixed coefficients regression in high dimensional setting when the effects are expected to be small but not zeros. This paper considers estimation and prediction of random coefficient ridge regression in the setting of transfer learning, where in addition to observations from the target model, source samples from different but possibly related regression models are available. The informativeness of the source model to the target model can be quantified by the correlation between the regression coefficients. This paper proposes two estimators of regression coefficients of the target model as the weighted sum of the ridge estimates of both target and source models, where the weights can be determined by minimizing the empirical estimation risk or prediction risk. Using random matrix theory, the limiting values of the optimal weights are derived under the setting when $p/n \rightarrow \gamma$, where $p$ is the number of the predictors and $n$ is the sample size, which leads to an explicit expression of the estimation or prediction risks. Simulations show that these limiting risks agree very well with the empirical risks. An application to predicting the polygenic risk scores for lipid traits shows such transfer learning methods lead to smaller prediction errors than the single sample ridge regression or Lasso-based transfer learning.