Algorithms for leader selection in stochastically forced consensus networks
Paper and Code
May 29, 2013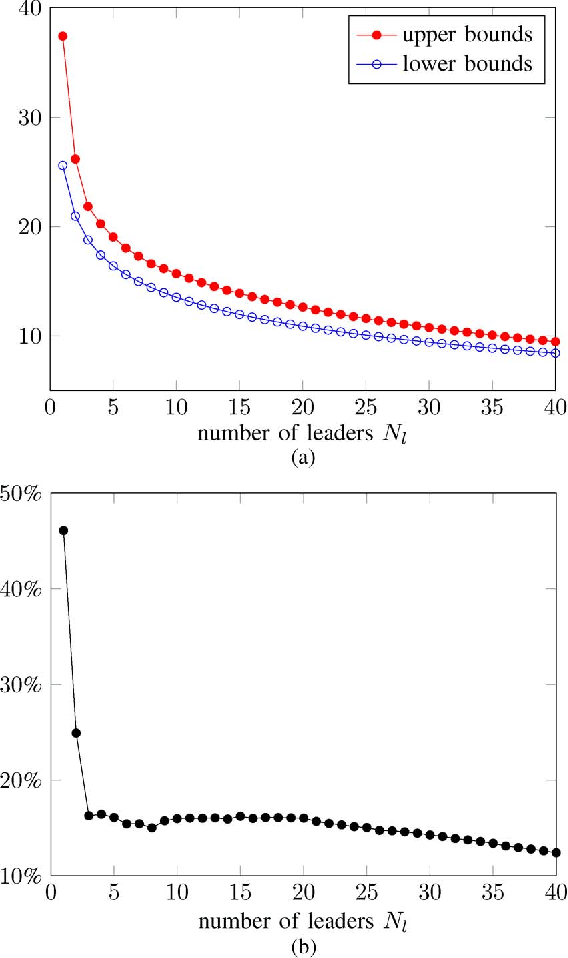
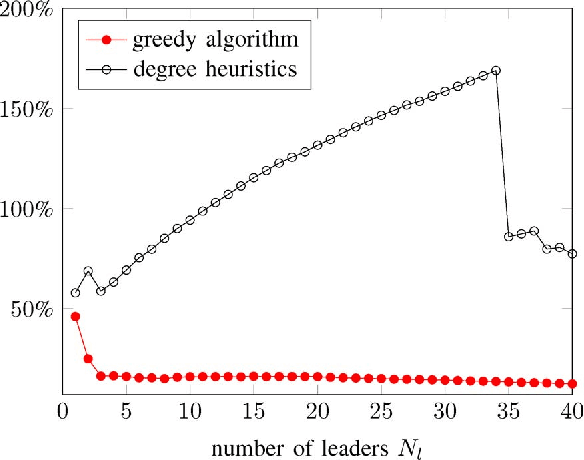
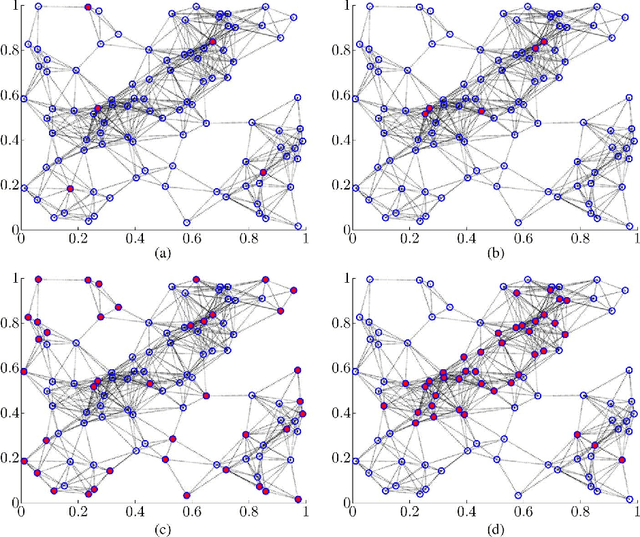
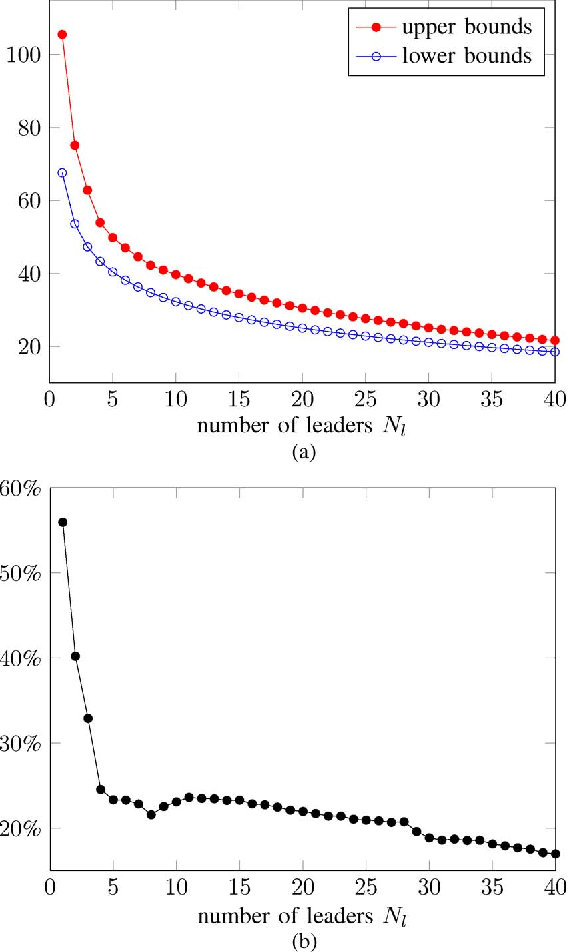
We are interested in assigning a pre-specified number of nodes as leaders in order to minimize the mean-square deviation from consensus in stochastically forced networks. This problem arises in several applications including control of vehicular formations and localization in sensor networks. For networks with leaders subject to noise, we show that the Boolean constraints (a node is either a leader or it is not) are the only source of nonconvexity. By relaxing these constraints to their convex hull we obtain a lower bound on the global optimal value. We also use a simple but efficient greedy algorithm to identify leaders and to compute an upper bound. For networks with leaders that perfectly follow their desired trajectories, we identify an additional source of nonconvexity in the form of a rank constraint. Removal of the rank constraint and relaxation of the Boolean constraints yields a semidefinite program for which we develop a customized algorithm well-suited for large networks. Several examples ranging from regular lattices to random graphs are provided to illustrate the effectiveness of the developed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge