Correcting False Alarms from Unseen: Adapting Graph Anomaly Detectors at Test Time

Graph anomaly detection (GAD), which aims to detect outliers in graph-structured data, has received increasing research attention recently. However, existing GAD methods assume identical training and testing distributions, which is rarely valid in practice. In real-world scenarios, unseen but normal samples may emerge during deployment, leading to a normality shift that degrades the performance of GAD models trained on the original data. Through empirical analysis, we reveal that the degradation arises from (1) semantic confusion, where unseen normal samples are misinterpreted as anomalies due to their novel patterns, and (2) aggregation contamination, where the representations of seen normal nodes are distorted by unseen normals through message aggregation. While retraining or fine-tuning GAD models could be a potential solution to the above challenges, the high cost of model retraining and the difficulty of obtaining labeled data often render this approach impractical in real-world applications. To bridge the gap, we proposed a lightweight and plug-and-play Test-time adaptation framework for correcting Unseen Normal pattErns (TUNE) in GAD. To address semantic confusion, a graph aligner is employed to align the shifted data to the original one at the graph attribute level. Moreover, we utilize the minimization of representation-level shift as a supervision signal to train the aligner, which leverages the estimated aggregation contamination as a key indicator of normality shift. Extensive experiments on 10 real-world datasets demonstrate that TUNE significantly enhances the generalizability of pre-trained GAD models to both synthetic and real unseen normal patterns.

Graph Wave Networks

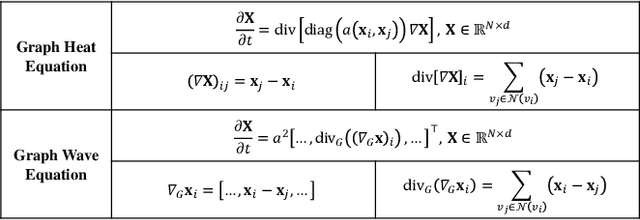
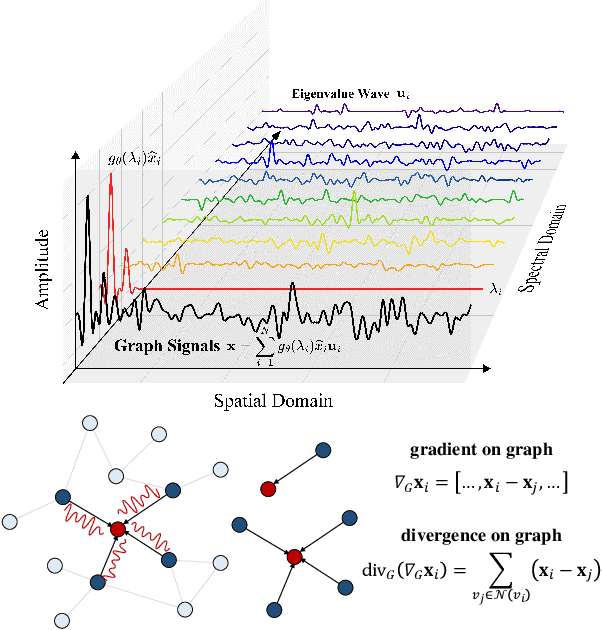
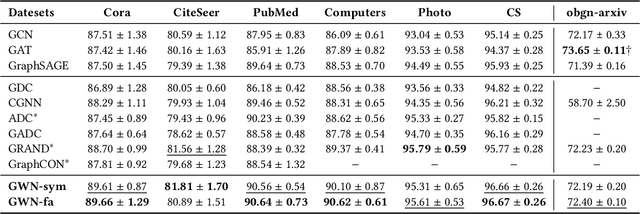
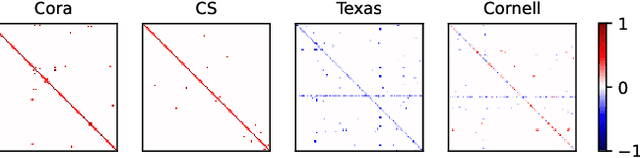
Dynamics modeling has been introduced as a novel paradigm in message passing (MP) of graph neural networks (GNNs). Existing methods consider MP between nodes as a heat diffusion process, and leverage heat equation to model the temporal evolution of nodes in the embedding space. However, heat equation can hardly depict the wave nature of graph signals in graph signal processing. Besides, heat equation is essentially a partial differential equation (PDE) involving a first partial derivative of time, whose numerical solution usually has low stability, and leads to inefficient model training. In this paper, we would like to depict more wave details in MP, since graph signals are essentially wave signals that can be seen as a superposition of a series of waves in the form of eigenvector. This motivates us to consider MP as a wave propagation process to capture the temporal evolution of wave signals in the space. Based on wave equation in physics, we innovatively develop a graph wave equation to leverage the wave propagation on graphs. In details, we demonstrate that the graph wave equation can be connected to traditional spectral GNNs, facilitating the design of graph wave networks based on various Laplacians and enhancing the performance of the spectral GNNs. Besides, the graph wave equation is particularly a PDE involving a second partial derivative of time, which has stronger stability on graphs than the heat equation that involves a first partial derivative of time. Additionally, we theoretically prove that the numerical solution derived from the graph wave equation are constantly stable, enabling to significantly enhance model efficiency while ensuring its performance. Extensive experiments show that GWNs achieve SOTA and efficient performance on benchmark datasets, and exhibit outstanding performance in addressing challenging graph problems, such as over-smoothing and heterophily.

Multi-modal and Multi-view Fundus Image Fusion for Retinopathy Diagnosis via Multi-scale Cross-attention and Shifted Window Self-attention

The joint interpretation of multi-modal and multi-view fundus images is critical for retinopathy prevention, as different views can show the complete 3D eyeball field and different modalities can provide complementary lesion areas. Compared with single images, the sequence relationships in multi-modal and multi-view fundus images contain long-range dependencies in lesion features. By modeling the long-range dependencies in these sequences, lesion areas can be more comprehensively mined, and modality-specific lesions can be detected. To learn the long-range dependency relationship and fuse complementary multi-scale lesion features between different fundus modalities, we design a multi-modal fundus image fusion method based on multi-scale cross-attention, which solves the static receptive field problem in previous multi-modal medical fusion methods based on attention. To capture multi-view relative positional relationships between different views and fuse comprehensive lesion features between different views, we design a multi-view fundus image fusion method based on shifted window self-attention, which also solves the computational complexity of the multi-view fundus fusion method based on self-attention is quadratic to the size and number of multi-view fundus images. Finally, we design a multi-task retinopathy diagnosis framework to help ophthalmologists reduce workload and improve diagnostic accuracy by combining the proposed two fusion methods. The experimental results of retinopathy classification and report generation tasks indicate our method's potential to improve the efficiency and reliability of retinopathy diagnosis in clinical practice, achieving a classification accuracy of 82.53\% and a report generation BlEU-1 of 0.543.

Multi-Modal Brain Tumor Segmentation via 3D Multi-Scale Self-attention and Cross-attention

Due to the success of CNN-based and Transformer-based models in various computer vision tasks, recent works study the applicability of CNN-Transformer hybrid architecture models in 3D multi-modality medical segmentation tasks. Introducing Transformer brings long-range dependent information modeling ability in 3D medical images to hybrid models via the self-attention mechanism. However, these models usually employ fixed receptive fields of 3D volumetric features within each self-attention layer, ignoring the multi-scale volumetric lesion features. To address this issue, we propose a CNN-Transformer hybrid 3D medical image segmentation model, named TMA-TransBTS, based on an encoder-decoder structure. TMA-TransBTS realizes simultaneous extraction of multi-scale 3D features and modeling of long-distance dependencies by multi-scale division and aggregation of 3D tokens in a self-attention layer. Furthermore, TMA-TransBTS proposes a 3D multi-scale cross-attention module to establish a link between the encoder and the decoder for extracting rich volume representations by exploiting the mutual attention mechanism of cross-attention and multi-scale aggregation of 3D tokens. Extensive experimental results on three public 3D medical segmentation datasets show that TMA-TransBTS achieves higher averaged segmentation results than previous state-of-the-art CNN-based 3D methods and CNN-Transform hybrid 3D methods for the segmentation of 3D multi-modality brain tumors.

A Two-Stage Pretraining-Finetuning Framework for Treatment Effect Estimation with Unmeasured Confounding

Estimating the conditional average treatment effect (CATE) from observational data plays a crucial role in areas such as e-commerce, healthcare, and economics. Existing studies mainly rely on the strong ignorability assumption that there are no unmeasured confounders, whose presence cannot be tested from observational data and can invalidate any causal conclusion. In contrast, data collected from randomized controlled trials (RCT) do not suffer from confounding, but are usually limited by a small sample size. In this paper, we propose a two-stage pretraining-finetuning (TSPF) framework using both large-scale observational data and small-scale RCT data to estimate the CATE in the presence of unmeasured confounding. In the first stage, a foundational representation of covariates is trained to estimate counterfactual outcomes through large-scale observational data. In the second stage, we propose to train an augmented representation of the covariates, which is concatenated to the foundational representation obtained in the first stage to adjust for the unmeasured confounding. To avoid overfitting caused by the small-scale RCT data in the second stage, we further propose a partial parameter initialization approach, rather than training a separate network. The superiority of our approach is validated on two public datasets with extensive experiments. The code is available at https://github.com/zhouchuanCN/KDD25-TSPF.

CL4KGE: A Curriculum Learning Method for Knowledge Graph Embedding

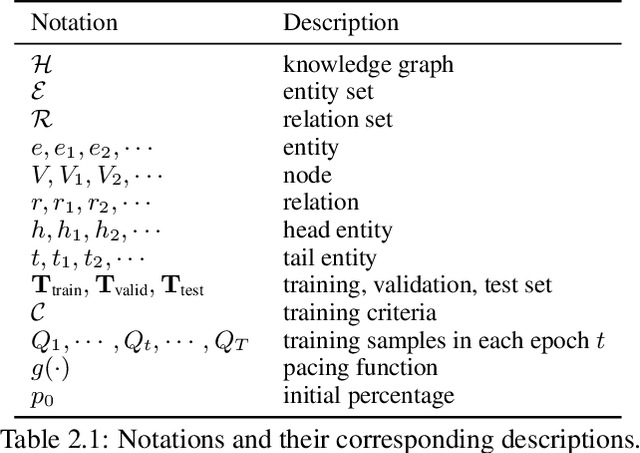
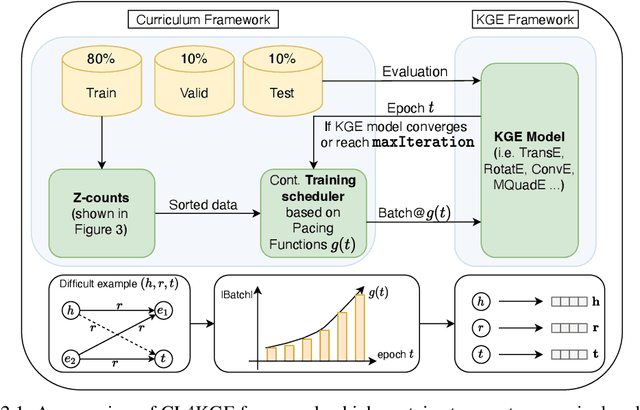
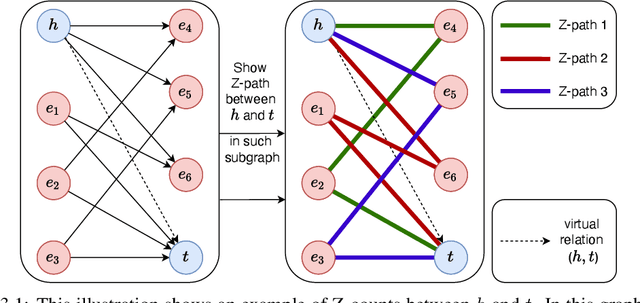
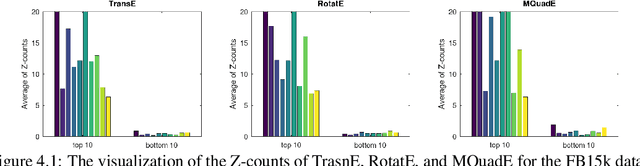
Knowledge graph embedding (KGE) constitutes a foundational task, directed towards learning representations for entities and relations within knowledge graphs (KGs), with the objective of crafting representations comprehensive enough to approximate the logical and symbolic interconnections among entities. In this paper, we define a metric Z-counts to measure the difficulty of training each triple ($<$head entity, relation, tail entity$>$) in KGs with theoretical analysis. Based on this metric, we propose \textbf{CL4KGE}, an efficient \textbf{C}urriculum \textbf{L}earning based training strategy for \textbf{KGE}. This method includes a difficulty measurer and a training scheduler that aids in the training of KGE models. Our approach possesses the flexibility to act as a plugin within a wide range of KGE models, with the added advantage of adaptability to the majority of KGs in existence. The proposed method has been evaluated on popular KGE models, and the results demonstrate that it enhances the state-of-the-art methods. The use of Z-counts as a metric has enabled the identification of challenging triples in KGs, which helps in devising effective training strategies.

Decision-focused Graph Neural Networks for Combinatorial Optimization

In recent years, there has been notable interest in investigating combinatorial optimization (CO) problems by neural-based framework. An emerging strategy to tackle these challenging problems involves the adoption of graph neural networks (GNNs) as an alternative to traditional algorithms, a subject that has attracted considerable attention. Despite the growing popularity of GNNs and traditional algorithm solvers in the realm of CO, there is limited research on their integrated use and the correlation between them within an end-to-end framework. The primary focus of our work is to formulate a more efficient and precise framework for CO by employing decision-focused learning on graphs. Additionally, we introduce a decision-focused framework that utilizes GNNs to address CO problems with auxiliary support. To realize an end-to-end approach, we have designed two cascaded modules: (a) an unsupervised trained graph predictive model, and (b) a solver for quadratic binary unconstrained optimization. Empirical evaluations are conducted on various classical tasks, including maximum cut, maximum independent set, and minimum vertex cover. The experimental results on classical CO problems (i.e. MaxCut, MIS, and MVC) demonstrate the superiority of our method over both the standalone GNN approach and classical methods.

Combinatorial Optimization with Automated Graph Neural Networks

In recent years, graph neural networks (GNNs) have become increasingly popular for solving NP-hard combinatorial optimization (CO) problems, such as maximum cut and maximum independent set. The core idea behind these methods is to represent a CO problem as a graph and then use GNNs to learn the node/graph embedding with combinatorial information. Although these methods have achieved promising results, given a specific CO problem, the design of GNN architectures still requires heavy manual work with domain knowledge. Existing automated GNNs are mostly focused on traditional graph learning problems, which is inapplicable to solving NP-hard CO problems. To this end, we present a new class of \textbf{AUTO}mated \textbf{G}NNs for solving \textbf{NP}-hard problems, namely \textbf{AutoGNP}. We represent CO problems by GNNs and focus on two specific problems, i.e., mixed integer linear programming and quadratic unconstrained binary optimization. The idea of AutoGNP is to use graph neural architecture search algorithms to automatically find the best GNNs for a given NP-hard combinatorial optimization problem. Compared with existing graph neural architecture search algorithms, AutoGNP utilizes two-hop operators in the architecture search space. Moreover, AutoGNP utilizes simulated annealing and a strict early stopping policy to avoid local optimal solutions. Empirical results on benchmark combinatorial problems demonstrate the superiority of our proposed model.

Phased Instruction Fine-Tuning for Large Language Models

Instruction Fine-Tuning, a method enhancing pre-trained language models' capabilities from mere next-word prediction to complex instruction following, often employs a one-off training approach on diverse instruction dataset. However, this method may not effectively enhance models' adherence to instructions due to the simultaneous handling of varying instruction complexities. To address this, we propose a novel phased instruction fine-tuning (Phased IFT) method, grounded in the hypothesis of progressive alignment, which posits that the transition of a pre-trained language model from simple next-word prediction to sophisticated instruction following is a gradual learning process. Specifically, we obtain the score of difficulty for each instruction via GPT-4, stratify the instruction data into subsets of increasing difficulty, and sequentially uptrain on these subsets using the standard supervised loss. Through extensive experiments on the pre-trained models Llama-2 7B/13B, and Mistral-7B using the 52K Alpaca instruction data, we demonstrate that Phased IFT significantly surpasses traditional one-off instruction fine-tuning (One-off IFT) method in win rate, empirically validating the progressive alignment hypothesis. Our findings suggest that Phased IFT offers a simple yet effective pathway for elevating the instruction-following capabilities of pre-trained language models. Models and datasets from our experiments are freely available at https://github.com/xubuvd/PhasedSFT.

GNNEvaluator: Evaluating GNN Performance On Unseen Graphs Without Labels

Evaluating the performance of graph neural networks (GNNs) is an essential task for practical GNN model deployment and serving, as deployed GNNs face significant performance uncertainty when inferring on unseen and unlabeled test graphs, due to mismatched training-test graph distributions. In this paper, we study a new problem, GNN model evaluation, that aims to assess the performance of a specific GNN model trained on labeled and observed graphs, by precisely estimating its performance (e.g., node classification accuracy) on unseen graphs without labels. Concretely, we propose a two-stage GNN model evaluation framework, including (1) DiscGraph set construction and (2) GNNEvaluator training and inference. The DiscGraph set captures wide-range and diverse graph data distribution discrepancies through a discrepancy measurement function, which exploits the outputs of GNNs related to latent node embeddings and node class predictions. Under the effective training supervision from the DiscGraph set, GNNEvaluator learns to precisely estimate node classification accuracy of the to-be-evaluated GNN model and makes an accurate inference for evaluating GNN model performance. Extensive experiments on real-world unseen and unlabeled test graphs demonstrate the effectiveness of our proposed method for GNN model evaluation.